Exercícios sobre energia e trabalho de uma força
(FGV SP/2006) Mantendo uma inclinação de 60º com o plano da lixa, uma pessoa arrasta sobre esta a cabeça de um palito de fósforos, deslocando-o com velocidade constante por uma distância de 5 cm, e ao final desse deslocamento, a pólvora se põe em chamas.
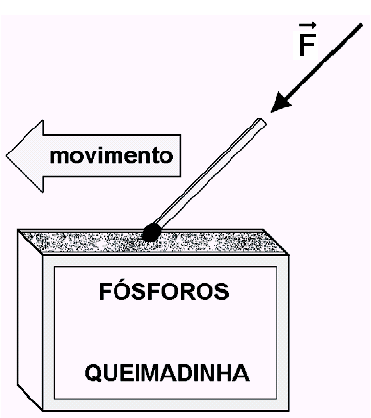
Se a intensidade da força, constante, aplicada sobre o palito é 2 N, a energia empregada no acendimento deste, desconsiderando-se eventuais perdas, é:
Dados: 
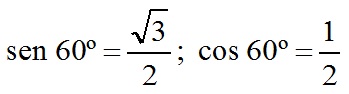
a) 5√3 x 10-2 J
b) 5 x 10-2 J
c) 2√3 x 10-2 J
d) 2 x 10-2 J
e) √3 x 10-2 J
Como o exercício nos orienta a desprezar eventuais perdas, podemos supor que toda energia será transferida para o palito.
Vamos utilizar a expressão do trabalho realizado pela força. A força realiza trabalho sobre o palito, esse trabalho é igual à variação da energia cinética do próprio palito.
T = F . d . cos θ
Logo: T = 2 x 0,05 x 0,5 = 0,05 J.
Expressando esse resultado em notação científica, temos:
T = 5 x 10-2J.
Alternativa “b”.
(Mackenzie SP/2006)
Uma caixa de massa m é abandonada do repouso, do topo do plano inclinado liso da figura. Essa caixa passa pelo ponto B e, devido ao atrito existente no trecho horizontal, para no ponto C.
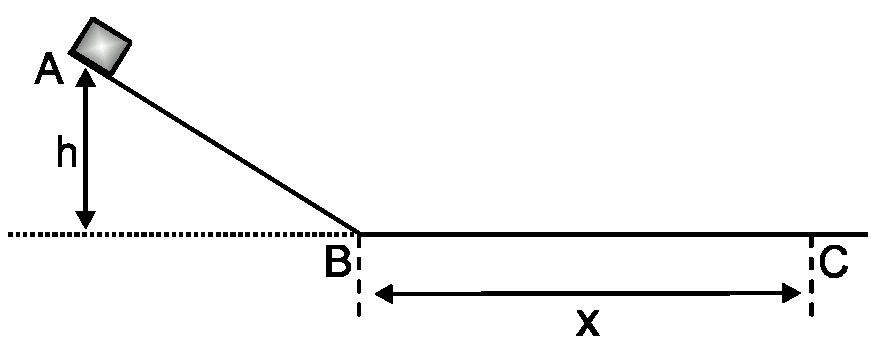
O coeficiente de atrito no trecho BC pode ser dado por:
a) μ = x
h
b) μ = h
x
c) μ = 2h
x
d) μ = x
h2
e) μ = 2x
h
Fazendo: Energia mecânica em A : Ea = Mgh
Energia mecânica em B: Eb = MVb²/2
temos que Ea = Eb, logo: Mgh = MVb²/2.
Dividindo os dois lados da equação por M e passando o 2 multiplicando, temos: Vb² = 2gh.
Sabendo que de B até C o movimento será retilíneo variado, podemos fazer:
Vb² = Vc² - 2α x (Equação de Torricelli)
2gh = 2αx, então α = -gh/x
Pela segunda lei de Newton temos que Fr = m.α, mas a partir do ponto B, a única força que atua sobre o bloco é a força de atrito cinético. Logo:
-μN = M.(-gh/x), onde N é força normal, que é perpendicular à superfície BC, e nesse caso tem módulo igual ao do peso Mg da caixa.
μ.Mg = Mgh/x
Então: μ = h/x.
Alternativa “b”.
Imagine a seguinte situação: um operário da construção civil precisa carregar um saco de cimento de 50 kg. Ele levanta esse saco de cimento e se desloca por 20 metros na horizontal. Adote g = 10 m/s². Calcule o trabalho realizado pela força do operário sobre o cimento.
a) 1000 J
b) 2500 J
c) 0 J
d) 10000J
e) 50 J
A resposta é zero. Embora o operário exerça uma força em módulo igual ao peso do saco de cimento, que é de 500 N, essa força é na vertical, enquanto seu deslocamento é na horizontal, ou seja, o ângulo entre a força e o deslocamento é 90°. Quando a força e o deslocamento formam um ângulo igual a 90°, o trabalho realizado por essa força é nulo. Veja: T = F . d . cos θ
θ = 90°, logo cos 90° = 0, então T = 0.
Alternativa "c".
Um objeto de massa 5 kg é deixado cair de uma determinada altura. Ele chega ao solo com energia cinética igual 2000 J. Determine a altura que o objeto foi abandonado. Despreze o atrito com o ar e considere g = 10 m/s²
Pela conservação da energia mecânica (E) temos:
Einicial = Efinal
No início só temos energia potencial gravitacional, pois o objeto é abandonado do repouso. No final , ao chegar no solo, toda energia potencial gravitacional se converteu em energia cinética. Então:
m .g. h = 2000, logo 5 . 10 . h = 2000
h = 2000/50
h = 40 m
