Exercícios sobre a Equação de Clapeyron
Determine o volume molar de um gás ideal, cujas condições estejam normais, ou seja, a temperatura à 273K e a pressão a 1 atm. (Dado: R = 0,082 atm.L/mol.K)
Substituindo os valores dados na equação para calcular o volume do mol do gás
pV = nRT
1.V = 1. 0,082. 273
V = 22,4 L
Determine o número de mols de um gás que ocupa volume de 90 litros. Este gás está a uma pressão de 2 atm e a uma temperatura de 100K. (Dado: R = 0,082 atm.L/mol.K)
Substituindo os valores dados na equação...
pV = nRT
2. 90 = n. 0,082. 100
180 = n. 8,2
n = 180 / 8,2
n = 21,95 mols
(Mackenzie- SP)
Um recipiente de volume V, totalmente fechado, contém 1 mol de um gás ideal, sob uma certa pressão p. A temperatura absoluta do gás é T e a constante universal dos gases perfeitos é R= 0,082 atm.litro/mol.K. Se esse gás é submetido a uma transformação isotérmica, cujo gráfico está representado abaixo, podemos afirmar que a pressão, no instante em que ele ocupa o volume é de 32,8 litros, é:
a) 0,1175 atm
b) 0,5875 atm
c) 0,80 atm
d) 1,175 atm
e) 1,33 atm
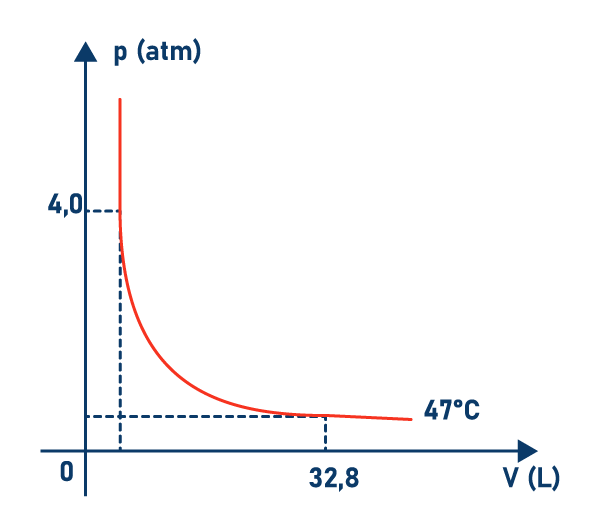
No estado final temos V = 32,8 L
Transformando a variação de temperatura Celsius para Kelvin, teremos:
T = θ + 273
T = 47 + 273
T = 320 K
Substituindo na eq. de Clapeyron
pV = nRT
p . 32,8 = 1. 0,082. 320
p = 0,80 atm
Resposta alternativa c
(PUC-SP)
Um certo gás, cuja massa vale 140g, ocupa um volume de 41 litros, sob pressão 2,9 atmosferas a temperatura de 17°C. O número de Avogadro vale 6,02. 1023 e a constante universal dos gases perfeitos R= 0,082 atm.L/mol.K.
Nessas condições, o número de moléculas continuadas no gás é aproximadamente de:
a) 3,00. 1024
b) 5,00. 1023
c) 6,02. 1023
d) 2,00. 1024
e) 3,00. 1029
Substituindo os valores dados na eq. de Clapeyron
pV = nRT
2,9. 41 = n. 0,082. 290
n = 5 mols
Usaremos regra de três simples para calcularmos o valor das moléculas
1 mol _______ 6,02 .1023 moléculas
5 mols ______ x
x ≈ 3,00. 1024 moléculas (note que este é um valor aproximado: houve a utilização da regra de arredondamento.)
Alternativa a
