Exercícios sobre expressões numéricas
A respeito da resolução de expressões numéricas, assinale a alternativa correta:
a) As operações devem ser feitas na ordem em que aparecem.
b) É necessário calcular primeiro todas as operações no interior dos parênteses na ordem em que elas aparecem.
c) A pessoa que realiza os cálculos escolhe a ordem mais oportuna para eles.
d) Não existe ordem para realização dos cálculos em uma expressão numérica.
e) As adições e subtrações são os últimos cálculos na lista de prioridades das expressões numéricas.
a) Falsa!
As operações devem ser feitas na seguinte ordem: potências e raízes, multiplicações e divisões e, por fim, adições e subtrações.
b) Falsa!
Embora realmente seja necessário calcular primeiro as operações no interior de parênteses, a ordem de realização das operações é: potências e raízes, multiplicações e divisões e, por fim, adições e subtrações.
c) Falsa!
A ordem para realização das operações é predefinida: potências e raízes, multiplicações e divisões e, por fim, adições e subtrações.
d) Falsa!
Na realidade, existe uma ordem de realização dos cálculos, como já dito.
e) Verdadeira!
Gabarito: letra E.
Qual das alternativas a seguir representa um quinto do resultado desta expressão numérica:
[(64 – 16·4) + (48·10 – 180)]·5
a) 270
b) 300
c) 350
d) 400
e) 410
Para resolver esse problema, lembre-se da ordem de resolução das expressões numéricas. Primeiramente, deve-se resolver o interior dos parênteses; em seguida, os colchetes e, nos casos em que aparecerem, as chaves. Já as operações matemáticas devem ser resolvidas com a seguinte prioridade: primeiramente, as raízes e potências (na ordem em que aparecerem); depois, multiplicações e divisões (na ordem em que aparecerem) e, por fim, adições e subtrações (na melhor ordem possível). Dessa maneira, faremos:
[(64 – 16·4) + (48·10 – 180)]·5 =
[(64 – 64) + (480 – 180)]·5 =
[0 + 300]·5 =
300·5 =
1500
Como o exercício pede um quinto desse resultado, será necessário dividi-lo por 5:
1500:5 = 300
Gabarito: letra B.
Analise a solução da expressão algébrica abaixo e assinale a alternativa correta:
{(10·10 + 4·11):12 – [(20 + 19·10):39 + 15]} + 50 =
{(100 + 44):12 – [(39·10):39 + 15]} + 50 =
{144:12 – [390:39 + 15]} + 50 =
{12 – [10 + 15]} + 50 =
{12 – 25} + 50 =
– 13 + 50 =
37
a) A resolução está correta, nenhum erro foi cometido.
b) A resolução está correta, mas por coincidência, pois alguns erros foram cometidos.
c) A resolução está incorreta, o verdadeiro resultado é 50.
d) A resolução está incorreta, pois foi feita uma soma em vez de dar prioridade a uma multiplicação.
e) A resolução está incorreta, pois as multiplicações devem ser feitas sempre depois das divisões.
a) Incorreta!
A resolução está incorreta e um erro foi cometido.
b) Incorreta!
A resolução está incorreta.
c) Incorreta!
O resultado não é 50.
d) Correta!
Observe que, logo no início, houve esta soma: 20 + 19 = 39. O correto seria primeiramente multiplicar 19·10 e, depois, somar 20 ao resultado.
e) Incorreta!
Não existe prioridade entre multiplicações e divisões.
Gabarito: letra D.
Margarida viu no quadro-negro algumas anotações da aula anterior um pouco apagadas, conforme mostra a figura a seguir. Qual número foi apagado?
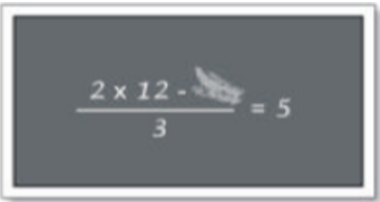
a) 9
b) 10
c) 12
d) 13
e) 15
Primeiramente, trocaremos x por ·, para representar a multiplicação, e o espaço apagado por y, para representar o número que queremos descobrir. Posteriormente, multiplicaremos ambos os lados da igualdade pelo mesmo número para obter:
2·12 – x = 5
3
2·12 – x = 5·3
2·12 – x = 15
24 – x = 15
Agora, pense em um número que subtraído de 24 resulte em 15, ou seja, um número que somado com 15 resulte em 24. Esse número é 9.
Gabarito: letra A.
