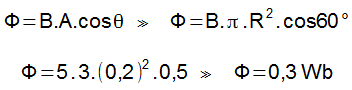Exercícios sobre fluxo magnético e Lei de Faraday
Esta lista de exercícios aborda a Lei de Faraday e o fluxo magnético, princípios relacionados ao estudo do Eletromagnetismo.
Publicado por: Joab Silas da Silva JúniorQuestões
-
Questão 1
(UCS-RS) A Costa Rica, em 2015, chegou muito próximo de gerar 100% de sua energia elétrica a partir de fontes renováveis, como a hídrica, a eólica e a geotérmica. A lei da Física que permite a construção de geradores que transformam outras formas de energia em energia elétrica é a Lei de Faraday, que pode ser mais bem definida pela seguinte declaração:
a) Toda carga elétrica produz um campo elétrico com direção radial, cujo sentido independe do sinal dessa carga.
b) Toda corrente elétrica, em um fio condutor, produz um campo magnético com direção radial ao fio.
c) Uma carga elétrica, em repouso, imersa em um campo magnético sofre uma força centrípeta.
d) A força eletromotriz induzida em uma espira é proporcional à taxa de variação do fluxo magnético em relação ao tempo gasto para realizar essa variação.
e) Toda onda eletromagnética torna-se onda mecânica quando passa de um meio mais denso para um menos denso.
Letra D
A alternativa D é o enunciado da Lei de Faraday, que pode ser representada da seguinte forma:
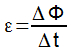
-
Questão 2
(UFJF-MG) Uma espira circular está imersa em um campo magnético criado por dois ímãs, conforme a figura abaixo. Um dos ímãs pode deslizar livremente sobre uma mesa, que não interfere no campo gerado. O gráfico da figura, a seguir, representa o fluxo magnético através da espira em função do tempo.
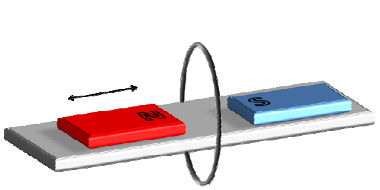
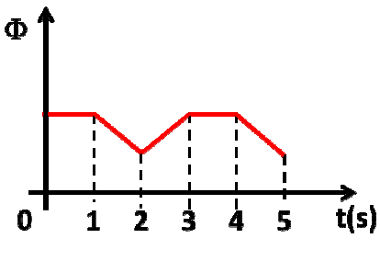
O intervalo de tempo em que aparece na espira uma corrente elétrica induzida é de:
a) De 0 a 1 s, somente.
b) De 0 a 1 s e de 3 s a 4 s.
c) De 1 s a 3 s e de 4 s a 5 s.
d) De 1 s a 2 s e de 4 s a 5 s.
e) De 2 s a 3 s, somente.
Letra C
Pela Lei de Faraday, pode-se compreender que só existirá corrente elétrica induzida quando houver variação de fluxo magnético (Φ). Ao observar o gráfico, percebemos que a variação de fluxo ocorre entre os instantes 1 s e 3 s e entre os instantes 4 s e 5 s.
-
Questão 3
Determine o fluxo magnético, em Wb, sobre uma espira quadrada com lado de 20 cm sob influência de um campo magnético perpendicular à reta normal ao plano dessa espira e de módulo 100 T.
a) 0
b) 5
c) 5,5
d) 10
e) 15
Letra A
O campo magnético é perpendicular ao plano da espira, o que significa que não existem linhas de campo magnético passando pelo material. Portanto, nesse caso, o fluxo magnético é nulo, conforme a representação a seguir:
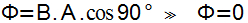
-
Questão 4
Uma espira circular de raio 0,2 m está sob influência de um campo magnético de módulo 5 T. Determine o fluxo magnético sobre a espira considerando que o ângulo entre o vetor campo magnético e a reta normal ao plano dessa espira seja de 60°.
Dados: π = 3, cos60° = 0,5.
a) 0,1
b) 0,2
c) 0,3
d) 0,4
e) 0,6
Letra C
O fluxo magnético sobre a espira pode ser calculado da seguinte forma: