Exercícios sobre força elétrica
Duas cargas puntiformes de valores \({Q}_\mathbf{1}=\mathbf{5}{\mu C}\) e \({Q}_\mathbf{2}=-\mathbf{10}{\mu C}\) estão a uma distância de 5 cm. Qual é a força elétrica entre elas? Determine também se ela é repulsiva ou atrativa.
A) 180 N, atrativa.
B) 100 N, repulsiva.
C) 180 N, repulsiva.
D) 1000 N, atrativa.
E) 1,8 N, atrativa.
Alternativa A
Encontraremos o valor da força elétrica utilizando a lei de Coulomb:
\(F=k\frac{\left|Q_1\right|\bullet\left|Q_2\right|}{d^2}\)
O F da fórmula é a força elétrica que queremos descobrir. A constante k vale \(9\ \bullet{10}^{9\ }N{\ m}^2\ /C^2\), a distância d será convertida de centímetros para metros (5 cm = 0,05 m) e as cargas foram dadas, portanto a fórmula fica da seguinte forma:
\(F=9\ \bullet{10}^{9\ }\frac{\left|5\mu C\right|\bullet\left|-10\mu C\right|}{{(0,05\ )}^2}\)
Substituiremos micro (\(\mu\)) pelo seu valor, de \({10}^{-6}\):
\(F=\ 9\ \bullet{10}^{9\ }\bullet\frac{\left|5\bullet{10}^{-6}\right|\bullet\left|-10\bullet{10}^{-6}\right|}{{(0,05)}^2}\)
Os módulos transformarão o sinal em positivo:
\(F=\ 9\ \bullet{10}^{9\ }\bullet\frac{5\bullet{10}^{-6}\bullet10\bullet{10}^{-6}}{{(0,05)}^2}\)
Por fim, resolveremos a conta:
\(F=\ 9\ \bullet{10}^{9\ }\bullet\frac{50\bullet{10}^{-6-6}\ }{0,0025}\)
\(F=\ 9\ \bullet{10}^{9\ }\bullet\frac{50\bullet{10}^{-12}\ }{0,0025}\)
\(F=\ \frac{9\bullet50\bullet{10}^{9-12}\ }{0,0025}\)
\(F=\ \frac{450\bullet{10}^{-3}\ }{0,0025}\)
\(F=\ 180000\bullet{10}^{-3}\)
\(F=\ 180\bullet{10}^3\bullet{10}^{-3}\)
\(F=\ 180\bullet{10}^{3-3}\)
\(F=\ 180\bullet{10}^0\)
\(F=\ 180\bullet1\)
\(F=\ 180\ N\)
A força elétrica é atrativa, porque as cargas possuem sinais contrários.
Uma carga elétrica com valor de \(10\ \mu C\) possui campo elétrico com valor de \(3,0\bullet{10}^5\ N/C\). Determine a força elétrica gerada.
A) \(3,0\bullet{10}^5\ N/C\)
B) \(10\bullet{10}^5\ N/C\)
C) \(3,0\bullet{10}^{-5}\ N/C\)
D) \(3,0\bullet{10}^{-6}\ N/C\)
E) \(3,0\bullet{10}^6\ N/C\)
Alternativa E
Usando a fórmula que relaciona a força elétrica com o campo elétrico, podemos obter o valor daquela:
\(F=\left|q\right|\bullet E\)
\(F=\left|10\right|\bullet3,0\bullet{10}^5\)
\(F=10\bullet3,0\bullet{10}^5\)
\(F=3,0\bullet{10}^{5+1}\)
\(F=3,0\bullet{10}^{6\ }N\)
Uma partícula possui campo elétrico com valor de \(200\bullet{10}^5\ N/C\) e força elétrica com valor de \(5,0\bullet{10}^5\ N\). Determine o valor da carga elétrica.
A) 0,025 C
B) 0,05 C
C) 0,055 C
D) 0,045 C
E) 0,035 C
Alternativa A
Usando a fórmula que relaciona a força elétrica com o campo elétrico, podemos obter o valor da força elétrica:
\(F=\left|q\right|\bullet E\)
\(5\bullet{10}^5=\left|q\right|\bullet200\bullet{10}^5\)
\(\frac{{5\bullet10}^5}{200\bullet{10}^5}\ =\left|q\right|\)
\(\frac{5}{200}\ =\left|q\right|\)
\(\frac{5}{200}\ =\left|q\right|\)
\(0,025\ C\ =\left|q\right|\)
Uma carga q e outra Q, com o dobro de q, estavam inicialmente a uma distância d e foram reposicionadas a uma distância equivalente ao dobro da inicial. A força elétrica final será de quanto da força inicial?
A) \({F}_{{final}}=\frac{{F}_{{inicial}}}{\mathbf{8}}\)
B) \({F}_{{final}}={{4}\bullet{F}}_{{inicial}}\)
C) \({F}_{{final}}=\frac{{F}_{{inicial}}}{\mathbf{4}}\)
D) \({F}_{{final}}={F}_{{inicial}}\)
E) \({F}_{{final}}={{8}\bullet{F}}_{{inicial}}\)
Alternativa C
Para compararmos o valor da força elétrica final com a força elétrica inicial, precisamos encontrar seus valores por meio da fórmula da lei de Coulomb:
\(F=k\frac{\left|Q_1\right|\bullet\left|Q_2\right|}{d^2}\)
A força elétrica inicial mede:
\(F_{inicial}=k\frac{\left|Q_1\right|\bullet\left|Q_2\right|}{d_{inicial}^2}\)
\(F_{inicial}=k\frac{\left|q\right|\bullet\left|Q\right|}{d_{inicial}^2}\)
\(Q=2q\), então:
\(F_{inicial}=k\frac{\left|q\right|\bullet\left|2q\right|}{d_{inicial}^2}\)
\(F_{inicial}=k\frac{2\bullet q^2}{d_{inicial}^2}\)
Já a força elétrica final mede:
\(F_{final}=k\frac{\left|Q_1\right|\bullet\left|Q_2\right|}{d_{final}^2}\)
\(F_{final}=k\frac{\left|q\right|\bullet\left|Q\right|}{d_{final}^2}\)
\(F_{final}=k\frac{\left|q\right|\bullet\left|2q\right|}{d_{final}^2}\)
\(F_{final}=k\frac{2\bullet q^2}{d_{final}^2}\)
A distâncial final é o dobro da distância inicial:
\(F_{final}=k\frac{2\bullet q^2}{\left({2d}_{inicial}\right)^2}\)
\(F_{final}=k\frac{2\bullet q^2}{4\bullet d_{inicial}^2}\)
Contudo, \(F_{inicial}=k\frac{2\bullet q^2}{d_{inicial}^2}\), então substituindo, conclui-se que:
\(F_{final}=\frac{F_{inicial}}{4}\)
A força final é a força inicial dividida por 4.
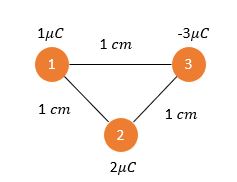
Três cargas elétricas estão espaçadas e com seus valores descritos na imagem abaixo:
Como as forças \({F}_{\mathbf{12}}\), \({F}_{\mathbf{23}}\) e \({F}_{\mathbf{31}}\) são classificadas?
A) São classificadas como repulsiva, atrativa e atrativa, respectivamente.
B) São classificadas como atrativa, atrativa e repulsiva, respectivamente.
C) São classificadas como atrativa, repulsiva e atrativa, respectivamente.
D) São classificadas como atrativas.
E) São classificadas como repulsivas.
Alternativa A
A força elétrica entre a carga 1 e a carga 2 é repulsiva, pois elas possuem o mesmo sinal. Já as forças entre as cargas 2 e 3 e entre 3 e 1 são atrativas, por possuírem sinais opostos.
Duas cargas iguais de \(50\bullet{10}^{-6}\ C\) se atraem no vácuo com uma força de \(200\ N\). Qual é a distância entre as cargas?
A) 10 m
B) 15 m
C) 30 m
D) 150 m
E) 50 m
Alternativa B
Usando a lei de Coulomb, conseguiremos determinar a distância entre as cargas elétricas:
\(F=k\frac{\left|Q_1\right|\ \bullet\left|Q_2\right|}{d^2}\)
Sabendo que a constante k vale \(9\ \bullet{10}^{9\ }N{\ m}^2\ /C^2\) e que as cargas se atraem, conclui-se que elas possuem sinais opostos:
\(200=\ 9\ \bullet{10}^{9\ }\bullet\frac{\left|50\bullet{10}^{-6}\right|\bullet\left|-50\bullet{10}^{-6}\right|}{d^2}\)
\(200=\ 9\ \bullet{10}^{9\ }\bullet\frac{\left|50\bullet{10}^{-6}\right|\bullet\left|50\bullet{10}^{-6}\right|}{d^2}\)
\(200\bullet d^2=\ 9\ \bullet{10}^{9\ }\bullet50\bullet{10}^{-6}\bullet50\bullet{10}^{-6}\)
\(200\bullet d^2=\ 9\ \bullet{10}^{9\ }\bullet\ 2500\bullet{10}^{-6-6}\)
\(200\bullet d^2=\ 22500\bullet{10}^{9-6-6}\ \)
\(200\bullet d^2=\ 22500\bullet{10}^{-3}\ \)
\(d^2=\frac{22500\bullet{10}^{-3}}{0,1}\)
\(d^2=225000\bullet{10}^{-3}\)
\(d^2=2,25\bullet{10}^5\bullet{10}^{-3}\)
\(d^2=2,25\bullet{10}^{5-3}\)
\(d^2=2,25\bullet{10}^2\)
\(d^2=225\)
\(d=\sqrt{225}\)
\(d=15\ m\ \)
Duas cargas iguais com valor Q distanciadas a 10 cm se repulsam no vácuo com uma força de 100 N . Sabendo que k= 9∙109 , qual o valor da carga Q?
A) + 1∙10-5 C e - 1∙10-5 C
B) ± 1,054∙10-5 C
C) + 1,054∙10-5 C
D) - 1,054∙10-5 C
E) + 1,054∙10-5 C e - 1,054∙10-5 C
Alternativa B
Encontraremos o valor da carga elétrica por meio da fórmula da lei de Coulomb:
\(F=k\frac{\left|Q_1\right|\bullet\left|Q_2\right|}{d^2}\)
\(F=k\frac{\left|Q\right|\bullet\left|Q\right|}{d^2}\)
Convertendo a distância de centímetros para metros (10 cm=0,1 m) , obtemos:
\(100=9\bullet{10}^9\bullet\frac{Q^2}{{0,1}^2}\)
\(100=9\bullet{10}^9\bullet\frac{Q^2}{0,01}\)
\(Q^2=\frac{100\bullet0,01}{9\bullet{10}^9}\)
\(Q^2=\frac{1}{9\bullet{10}^9}\)
\(Q^2\approx1,11\bullet{10}^{-10}\)
\(Q\approx\pm\ 1,054\bullet{10}^{-5}\ C\)
As duas cargas valem aproximadamente 1,054∙10-5 C com sinal positivo ou ambas possuem esse valor com sinal negativo. Não há como determinar isso, porque ambas estão se repulsando.
Se multiplicarmos a força elétrica final em quatro vezes da força elétrica inicial de duas cargas q, quanto valerá a distância inicial comparada à distância final?
A) Ambas as distâncias serão iguais.
B) A distâncial inicial será quatro vezes a distâncial final.
C) A distâncial final será quatro vezes a distâncial inicial.
D) A distâncial final será o dobro da distâncial inicial.
E) A distâncial inicial será o dobro da distâncial final.
Alternativa E
Para fazermos a comparação entre as forças final e inicial, utilizaremos a fórmula da lei de Coulomb:
\(F=k\frac{\left|Q_1\right|\ \bullet\left|Q_2\right|}{d^2}\)
Isolaremos o valor de k, que será o mesmo inicialmente e no final.
\(k=\ \frac{F\bullet d^2}{\left|Q_1\right|\bullet\left|Q_2\right|}\)
Portanto:
\(k_{inicial}=k_{final}\)
\(\frac{F_{inicial}\bullet d_{inicial}^2}{\left|Q\right|\ \bullet\left|Q\right|}=\frac{F_{final}\bullet d_{final}^2}{\left|Q\right|\ \bullet\left|Q\right|}\)
Como o valor das cargas é o mesmo, podemos eliminá-las da conta:
\(F_{inicial}\bullet d_{inicial}^2=F_{final}\bullet d_{final}^2\)
Já que a força final é quatro vezes a força inicial, temos:
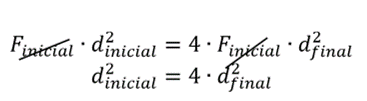
Utilizando a raiz quadrada em ambos os lados, obtemos:
\(d_{inicial}=2\bullet d_{final}\)
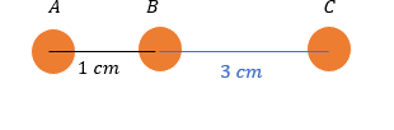
(Fuvest — adaptada) Três objetos com cargas elétricas idênticas estão alinhados como mostra a figura. O objeto C exerce sobre B uma força igual a 3,0∙10-6 N. A força elétrica resultante dos efeitos de A e C sobre B é de:
A) 2,0·10-6 N.
B) 6,0·10-6 N.
C) 12·10-6 N.
D) 24·10-6 N.
E) 30·10-6 N.
Alternativa D
Primeiramente, analisaremos a partícula C em relação à partícula B. A força entre essas partículas é de 3,0∙10-6N . Então substituiremos na fórmula da lei de Coulomb para encontrar o valor da carga elétrica:
\(F_{CB}=k\frac{\left|Q_1\right|\ \bullet\left|Q_2\right|}{d^2}\)
Como as cargas são iguais, convertendo de centímetro para metro e substituindo os valores referentes, temos:
\(3,0\bullet{10}^{-6}=9\bullet{10}^9\frac{\ Q^2}{\left(3\bullet{10}^{-2}\right)^2}\)
\(3,0\bullet{10}^{-6}=9\bullet{10}^9\frac{\ Q^2}{9\bullet{10}^{-4}}\)
\(3,0\bullet{10}^{-6}={10}^{9+4}{\bullet Q}^2\)
\(3,0\bullet{10}^{-6}={10}^{13}{\bullet Q}^2\)
\(\frac{3,0\bullet{10}^{-6}}{{10}^{13}}=Q^2\)
\(3,0\bullet{10}^{-6-13}=Q^2\)
\(3,0\bullet{10}^{-19}C=Q^2\)
Agora, descobriremos a força que A faz em B:
\(F_{AB}=k\frac{\left|Q_1\right|\bullet\left|Q_2\right|}{d^2}\)
\(F_{AB}=k\frac{Q^2}{d^2}\)
\(F_{AB}=9\bullet{10}^9\frac{\ 3,0\bullet{10}^{-19}}{\left(1\bullet{10}^{-2}\right)^2}\)
\(F_{AB}=9\bullet{10}^9\frac{3,0\bullet{10}^{-19}}{1\bullet{10}^{-4}}\)
\(F_{AB}=9\bullet{10}^9\bullet3,0\bullet{10}^{-19+4}\)
\(F_{AB}=27\bullet{10}^9\bullet{10}^{-15}\)
\(F_{AB}=27\bullet{10}^{9-16}\)
\(F_{AB}=27\bullet{10}^{-6}N\)
Assim, a força resultante em B é dada pela soma entre a força em A com a força em C. Como elas têm sentidos opostos, em razão de as cargas possuírem o mesmo sinal, a soma se torna uma subtração:
\(F_B=F_{AB}-F_{CB}\)
\(F_B=27,0\bullet{10}^{-6}-3,0\bullet{10}^{-6}\)
\(F_B=24,0\bullet{10}^{-6}\ N\)
(Cesgranrio) A lei de Coulomb afirma que a força de intensidade elétrica de partículas carregadas é proporcional:
I. às cargas das partículas;
II. às massas das partículas;
III. ao quadrado da distância entre as partículas;
IV. à distância entre as partículas.
Das afirmações acima
A) somente I é correta.
B) somente I e III são corretas.
C) somente II e III são corretas.
D) somente II é correta.
E) somente I e IV são corretas.
Alternativa A
A fórmula da lei de Coulomb é:
\(F=k\frac{\left|Q_1\right|\bullet\left|Q_2\right|}{d^2}\)
Por meio dela, vemos que a força é proporcional às cargas elétricas e inversamente proporcional ao quadrado da distância entre as partículas. Podemos desconsiderar a massa da partícula, por não ser relevante ao cálculo da força elétrica.
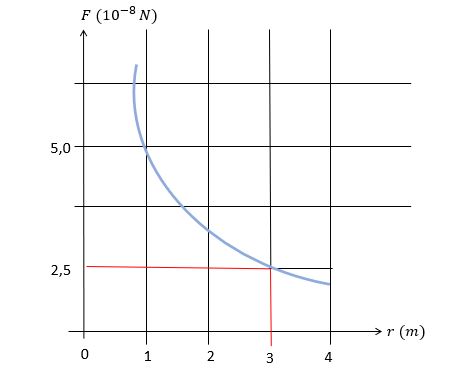
(UFPE — adaptada) O gráfico a seguir representa a força F entre duas cargas puntiformes positivas de mesmo valor, separadas pela distância r. Considere k=9 ∙109 N m2 /C2 e determine o valor das cargas, em unidades de 10-9 C.
A) 1,0
B) 2,0
C) 3,0
D) 4,0
E) 5,0
Alternativa E
Encontraremos o valor das cargas elétricas por meio da lei de Coulomb:
\(F=k\frac{\left|Q_1\right|\bullet\left|Q_2\right|}{d^2}\)
Podemos observar no gráfico que existe um ponto na curva que é comum à força e à distância, portanto usaremos o valor da força como F=2,5∙10-4 e a distância r=3 :
\(2,5\bullet{10}^{-8}=9\ \bullet{10}^9\frac{\left|Q_1\right|\bullet\left|Q_2\right|}{3^2}\)
Como as cargas são iguais, podemos multiplicá-las:
\(2,5\bullet{10}^{-8}=9\ \bullet{10}^9\frac{Q^2}{3^2}\)
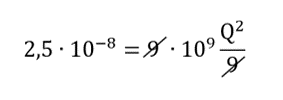
\(2,5\bullet{10}^{-8}={10}^9\bullet{Q}^2\)
\(\frac{2,5\bullet{10}^{-8}}{{10}^9}=Q^2\)
\(2,5\bullet{10}^{-8-9}=Q^2\)
\(2,5\bullet{10}^{-17}=Q^2\)
\(25\bullet{10}^{-1}\bullet{10}^{-17}=Q^2\)
\(25\bullet{10}^{-1-17}=Q^2\)
\(25\bullet{10}^{-18}=Q^2\)
\(\sqrt{25\bullet{10}^{-18}}=Q\)
\(5\bullet{10}^{-9}C=Q\)
(PUC-Rio) Dois objetos metálicos esféricos idênticos, contendo cargas elétricas de 1 C e de 5 C, são colocados em contato e depois afastados a uma distância de 3 m. Considerando a constante de Coulomb \(k=9\bullet{10}^9\ N{\ m}^2\ /C^2\) , podemos dizer que a força que atua entre as cargas após o contato é:
A) atrativa e tem módulo 3∙109N .
B) atrativa e tem módulo 9∙109N .
C) repulsiva e tem módulo 3∙109N .
D) repulsiva e tem módulo 9∙109N .
E) zero.
Alternativa D
Primeiramente, analisaremos as cargas elétricas. A partir disso, é possível ver que, como elas estão em contato, haverá uma troca de elétrons entre elas que só finalizará quando ambas estiverem com o mesmo valor de carga elétrica. Para encontrarmos esse valor, faremos uma média aritmética entre as cargas:
\(\frac{5+1}{2}=\frac{6}{2}=3\ C\)
Com os valores das cargas em mãos, substituiremos na fórmula da lei de Coulomb a fim de encontrar a força elétrica:
\(F=k\frac{\left|Q_1\right|\bullet\left|Q_2\right|}{d^2}\)
\(F=9\bullet{10}^9\bullet\frac{\left|3\right|\bullet\left|3\right|}{3^2}\)
\(F=9\bullet{10}^9\bullet\frac{9}{9}\)
\(F=9\bullet{10}^9N\)
