Exercícios sobre Hidrodinâmica
(ITA-SP – adaptada) Álcool, cuja densidade de massa é de 0,80 g/cm3, está passando através de um tubo, como mostra a figura.
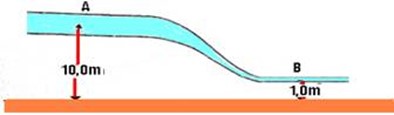
A secção reta do tubo em A é 2 vezes maior do que em B. Em A a velocidade é de \(v_A\ =\ 5,0\ m/s\); a altura, \(h_A=\ 10,0\ m\); e a pressão, \(p_A=\ 7,0\cdot{10}^3\ N/m^2\). Se a altura em B é \(h_B=\ 1,0\ m\), calcule a velocidade e a pressão em B.
a) 3,0 ∙104 N/m2
b) 4,9 ∙104 N/m2
c) 4,9 ∙104 N/m2
d) 4,9 ∙104 N/m2
e) 4,9 ∙104 N/m2
LETRA B
Primeiro, transformaremos a densidade de g/cm3 para kg/m3:
\(\frac{0,80\ g}{{cm}^3}=\frac{800\ kg}{m^3}\)
O enunciado menciona que a secção reta do tubo em A é 2 vezes maior do que em B. A partir dessa informação calcularemos a velocidade no ponto B através da equação da continuidade:
\(A_1\cdot v_1=A_2\cdot v_2\)
\(2A_2\cdot5=A_2\cdot v_2\)
\(v_2=\frac{2A_2\cdot5}{A_2}\)
\(v_2=2\cdot5\)
\(v_2=10\ m/s\)
Então, calcularemos a pressão em B, através do princípio de Bernoulli:
\(p_1+\frac{\rho\cdot v_1^2}{2}+\rho\cdot g\cdot y_1=p_2+\frac{\rho\cdot v_2^2}{2}+\rho\cdot g\cdot y_2\)
\(7,0\cdot{10}^3+\frac{800\ \cdot5^2}{2}+800\ \cdot10\cdot10=p_2+\frac{800\ \cdot{10}^2}{2}+800\ \cdot10\cdot1\)
\(7000+\frac{800\ \cdot25}{2}+80000=p_2+\frac{800\ \cdot100}{2}+8000\)
\(7000+10000+80000=p_2+40000+8000\)
\(97000=p_2+48000\)
\(p_2=97000-48000\)
\(p_2=49000\)
\(p_2=4,9\ \cdot{10}^4\ N/m^2\ \)
(UFSM-RS) A figura representa uma tubulação horizontal em que escoa um fluido ideal.
A velocidade de escoamento do fluido no ponto 1 em relação à velocidade verificada no ponto 2 e a pressão no ponto 1 em relação à pressão no ponto 2 são:
a) maior, maior
b) maior, menor
c) menor, maior
d) menor, maior
e) menor, menor
LETRA C
Analisaremos as velocidades através da fórmula da vazão volumétrica:
\(R_v=A\cdot v\)
\(A=\frac{R_v}{v}\)
A partir dela podemos observar que a área da seção de escoamento é inversamente proporcional à velocidade, então a velocidade no ponto 1 é menor do que a velocidade no ponto 2, já que a área da seção de escoamento no ponto 1 é maior do que no ponto 2.
De acordo com o princípio de Bernoulli, a pressão é inversamente proporcional à pressão, então se a velocidade no ponto 1 é menor do que no ponto 2, a pressão no ponto 1 é maior do que no ponto 2.
(UFPA – adaptada) Considere duas regiões distintas do leito de um rio: uma larga A, com 200 m2 de área de secção transversal, onde a velocidade escalar média da água é de 1,0 m/s, e outra estreita B, com 40 m2 de área de secção transversal. Calcule a vazão volumétrica do rio e a velocidade escalar média da água do rio na região estreita B.
a) 100 m3/s e 5 m/s
b) 200 m3/s e 5 m/s
c) 100 m3/s e 10 m/s
d) 200 m3/s e 10 m/s
e) 300 m3/s e 2 m/s
LETRA B
Primeiramente, calcularemos a vazão volumétrica através da sua fórmula:
\(R_v=A\cdot v\)
\(R_v=200\cdot1\ \)
\(R_v=200\ {m^3}/{s}\)
Depois, calcularemos a velocidade escalar média da água do rio na região estreita B, através da fórmula da vazão volumétrica:
\(R_v=A\cdot v\)
\(200=40\cdot v\)
\(v=\frac{200}{40}\)
\(v=5\ m/s\)
(Unama-AM) Uma piscina, cujas dimensões são 18 m x 10 m x 2 m, está vazia. O tempo necessário para enchê-la é 10h, através de um conduto de seção A = 25 cm². A velocidade da água, admitida constate, ao sair do conduto, terá modulo igual a:
a) 1 m/s
b) 2 km/s
c) 3 cm/s
d) 4 m/s
e) 5 km/s
LETRA D
Primeiro, converteremos o tempo para encher a piscina de horas para segundos e a área de secção de centímetros quadrados para metros quadrados:
\(∆t=10 horas=36000 s\)
\(A=25\ {cm}^2=0,0025\ m^2\)
Depois, calcularemos a vazão volumétrica, dada pelo volume da piscina pelo tempo que leva para enchê-la:
\(R_v=\frac{V}{∆t}\)
\(R_v=\frac{18\cdot10\cdot2}{36000}\)
\(R_v=0,01\ {m^3}/{s}\)
Por fim, calcularemos a velocidade da água através da fórmula da vazão volumétrica:
\(R_v=A\cdot v\)
\(0,01=0,0025\ \cdot v\)
\(v=\frac{0,01}{0,0025}\)
\(v=4\ m/s\)
Calcule a vazão de um fluido que escoa com velocidade média de 5,4 m/min através de uma tubulação de área de secção igual a 100 m2 .
a) 9 m3/s
b) 12 m3/s
c) 15 m3/s
d) 18m3/s
e) 21m3/s
LETRA A
Primeiro, converteremos a velocidade média de m/min para m/s:
\(v=\frac{5,4\ m}{1\ min}=\frac{5,4\ m}{60\ s}=0,09\ m/s\)
Por fim, calcularemos a vazão do fluido através da fórmula da vazão volumétrica:
\(R_v=A\cdot v\)
\(R_v=100\cdot0,09\ \)
\(R_v=9\ {m^3}/{s}\ \)
Determine a vazão mássica quando um fluido de densidade 850 kg/m3 passa a uma velocidade de 5 m/s por uma área da seção de escoamento de 10 m2.
a) 36 000
b) 42 500
c) 53 700
d) 60 800
e) 71 900
LETRA B
Calcularemos a vazão mássica através da sua fórmula:
\(R_m=\rho\cdot A\cdot v\)
\(R_m=850\cdot10\cdot5\)
\(R_m=42\ 500\ kg/s\)
Qual parte da Física é responsável por estudar os fluidos em movimento?
a) Termodinâmica.
b) Calorimetria.
c) Termologia.
d) Hidrostática.
e) Hidrodinâmica.
LETRA E
A Hidrostática é a parte da Física que visa investigar os fluidos em movimento. Para saber mais sobre essa área da Física, clique aqui.
Qual deve ser a área da seção de escoamento no ponto A de um tubo que possui uma área da seção de escoamento no ponto B de 4 m2, sabendo que a velocidade de escoamento no ponto A é de 12 m/s e no ponto B é de 9 m/s ?
a) 3 m2
b) 4 m2
c) 5 m2
d) 6 m2
e) 7 m2
LETRA A
Calcularemos a área da seção de escoamento no ponto A através da equação da continuidade:
\(A_A\cdot v_A=A_B\cdot v_B\)
\(A_A\cdot12=4\cdot9\)
\(A_A=\frac{4\cdot9}{12}\)
\(A_A=3\ m^2\)
Sabendo que a vazão volumétrica de certo fluido é 20 m3/s, determine a vazão mássica dele, considerando que a sua densidade seja de 750 kg/m3.
a) 7 500 kg/s
b) 10 200 kg/s
c) 15 000 kg/s
d) 18 600 kg/s
e) 25 300 kg/s
LETRA C
Primeiramente, encontraremos a relação entre a vazão volumétrica e a vazão mássica, através de suas fórmulas:
\(R_v=A\cdot v\)
\(R_m=\rho\cdot A\cdot v\)
Podemos observar que:
\(R_m=\rho\cdot R_v\)
Então a vazão mássica do fluido é:
\(R_m=750\cdot20\)
\(R_m=15\ 000\ kg/s\)
Qual deve ser a vazão em massa de um fluido que escoa em uma tubulação de 4m2 de área com velocidade de escoamento de 120 mm/min?
Dados: densidade do fluido = 1500 kgm3
a) 10 m3/s
b) 12 m3/s
c) 14 m3/s
d) 16 m3/s
e) 18 m3/s
LETRA B
Primeiramente, converteremos a velocidade de escoamento de mm/min para m/s:
\(v=\frac{120\ mm}{1\ min}=\frac{0,12\ m}{60\ s}=0,002\ m/s\)
Calcularemos a vazão mássica através da sua fórmula:
\(R_m=\rho\cdot A\cdot v\)
\(R_m=1500\cdot4\cdot0,002\ \)
\(R_m=12\ {m^3}/{s}\ \)
Em um tubo, conforme mostra a imagem, temos a passagem de água do ponto 1 ao ponto 2. Sabendo que a área da seção de escoamento em 1 é de 20 m2, a área da seção de escoamento em 2 é de 10 m2 e que a velocidade de escoamento em 1 é de 15 m/s, qual deve ser a velocidade de escoamento no ponto 2?
a) 5 m/s
b) 10 m/s
c) 20 m/s
d) 30 m/s
e) 40 m/s
LETRA D
Calcularemos a velocidade de escoamento no ponto 2, através da equação da continuidade:
\(A_1\cdot v_1=A_2\cdot v_2\)
\(20\cdot15=10\cdot v_2\)
\(300=10\cdot v_2\)
\(v_2=\frac{300}{10}\)
\(v_2=30\ m/s\)
Os tubos de pitot são equipamentos instalados em aeronaves civis e militares com o intuito de mensurar a velocidade dos aviões. Sabendo isso, em que parte da Hidrodinâmica estudamos o princípio que fundamenta o seu funcionamento?
a) Vazão volumétrica.
b) Equação da continuidade.
c) Princípio de Bernoulli.
d) Vazão mássica.
e) Princípio Fundamental da Dinâmica.
LETRA C
O estudo do princípio de Bernoulli permitiu o desenvolvimento dos tubos de pitot nos aviões.
