Exercícios sobre as leis de Ohm
Para resolver estes exercícios sobre as leis de Ohm, lembre-se das fórmulas usadas para calcular as grandezas físicas presentes nos elementos de um circuito elétrico.
Publicado por: Pâmella Raphaella MeloQuestões
-
Questão 1
(Unifesp-SP - adaptada) A linha de transmissão que leva energia elétrica da caixa de relógio até uma residência consiste de dois fios de cobre com 10,0 m de comprimento e secção reta com área 4,0 mm2 cada um. Considerando que a resistividade elétrica do cobre é ρ=1,6∙10-8Ω∙m, calcule a resistência elétrica r de cada fio desse trecho do circuito.
a) 0,01 Ω
b) 0,02 Ω
c) 0,03 Ω
d) 0,04 Ω
e) 0,05 Ω
LETRA D
Primeiramente, transformaremos a área de secção reta de milímetros quadrados para metros quadrados:
\(4,0 mm^2=4\cdot10^{-6} m^2\)
Depois, calcularemos a resistência elétrica por meio da fórmula da 2ª lei de Ohm:
\(R=ρ\cdot \frac{L}{A}\)
\(R=1,6\cdot10^{-8}\cdot\frac{10}{4\cdot10^{-6}}\)
\(R=\frac{16\cdot10^-8}{4\cdot10^-6}\)
\(R=4\cdot10^{-8+6}\)
\(R=4\cdot10 ^{-2}\)
\(R=0,04 Ω\)
-
Questão 2
(Mackenzie-SP) Um fio A tem resistência elétrica igual a duas vezes a resistência elétrica de um outro fio B. Sabe-se que o fio A tem o dobro do comprimento do fio B e sua seção transversal têm raio igual à metade do raio da seção transversal do fio B. A relação \(\frac{ρ_A}{ρ_B }\) entre a resistividade do material do fio A e a resistividade do material do fio B é:
a) 0,25
b) 0,50
c) 0,75
d) 1,25
e) 1,50
LETRA A
Calcularemos as resistividades elétricas do fio A e do fio B por meio da fórmula da 2ª lei de Ohm:
\(R=ρ\cdot\frac {L}{A}\)
Para facilitar a resolução, isolaremos a resistividade elétrica na fórmula, então:
\(R=ρ\cdot\frac {R \cdot A}{L}\)
Como se pede a relação ρAρB entre as resistividades elétricas do fio A e do fio B, então basta dividirmos uma pela outra:
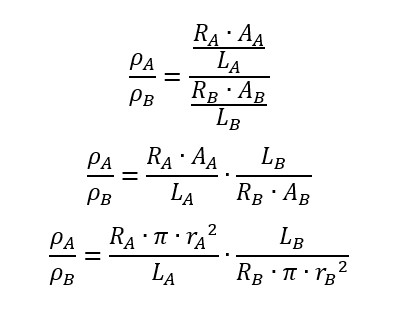
Pelo enunciado, obtemos:
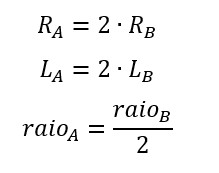
Então, substituindo na relação:
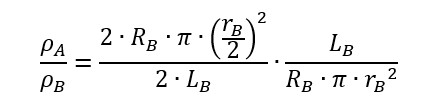
Eliminando os termos semelhantes:
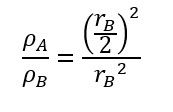
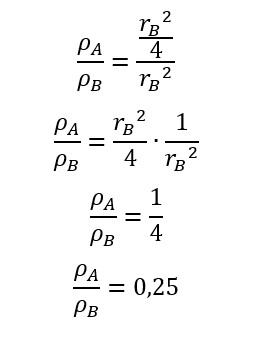
-
Questão 3
(Uneb-BA) Um resistor ôhmico, quando submetido a uma ddp de 40 V, é atravessado por uma corrente elétrica de intensidade 20 A. Quando a corrente que o atravessa for igual a 4 A, a ddp, em volts, nos seus terminais, será:
a) 8
b) 12
c) 16
d) 20
e) 30
LETRA A
Primeiramente, calcularemos a resistência do resistor por meio da fórmula da 1ª lei de Ohm:
\(U=R\cdot i\)
\(40=R\cdot20\)
\(R=\frac {40}{20}\)
\(R=2 Ω\)
Depois, calcularemos a tensão elétrica quando esse resistor é atravessado por uma nova corrente de 4 A, utilizando novamente a fórmula da 1ª lei de Ohm:
\(U=R\cdot i\)
\(U=2\cdot4\)
\(U=8 V\)
-
Questão 4
(UEL) Um resistor de 10 Ω, no qual flui uma corrente elétrica de 3,0 ampères, está associado em paralelo com outro resistor. Sendo a corrente elétrica total, na associação, igual a 4,5 ampères, o valor do segundo resistor, em ohms, é:
a) 5,0
b) 10
c) 20
d) 30
e) 60
LETRA C
Primeiramente, calcularemos a tensão elétrica, de 10 Ω, no resistor percorrido pela corrente de 3 A por meio da fórmula da 1ª lei de Ohm:
\(U=R\cdot i\)
\(U=10\cdot3\)
\(U=30 V\)
Como o primeiro resistor está em paralelo com o segundo, as suas tensões elétricas serão iguais, então calcularemos a resistência do segundo resistor por meio da fórmula da 1ª lei de Ohm:
\(U=R\cdot i \)
A corrente do segundo resistor será a corrente total menos a corrente do primeiro resistor, então:
\(30=R\cdot(4,5-3)\)
\(30=R\cdot1,5\)
\(R=\frac{30}{1,5}\)
\(R=20 Ω\)
-
Questão 5
De acordo com as leis de Ohm, a resistência elétrica é:
a) inversamente proporcional à tensão elétrica.
b) proporcional à resistividade elétrica.
c) proporcional à corrente elétrica.
d) inversamente proporcional ao comprimento do fio.
e) proporcional à área de secção transversal.
LETRA B
Com base na fórmula da 1ª lei de Ohm, temos que a resistência elétrica é proporcional à tensão elétrica e inversamente proporcional à corrente elétrica. Já por meio da fórmula da 2ª lei de Ohm, podemos observar que a resistência elétrica é proporcional à resistividade elétrica e ao comprimento do fio, mas inversamente proporcional à área de secção transversal.
-
Questão 6
Um resistor de 7,5∙10-5Ω é percorrido por uma corrente elétrica com valor de 10 A. A tensão elétrica entre os terminais do resistor é:
a) 7,0∙10-3 V
b) 7,5∙10-4 V
c) 8,0∙10-5 V
d) 8,5∙10-6 V
e) 9,0∙10-7 V
LETRA B
Calcularemos a tensão elétrica por meio da fórmula da 1ª lei de Ohm:
\(U=R\cdot i\)
\(U=7,5\cdot10^{-5}\cdot10\)
\(U=7,5\cdot10^{-5+1}\)
\(U=7,5\cdot10^{-4} V\)
-
Questão 7
O que acontece com a resistividade elétrica quando não variamos o comprimento e a área de secção transversal de um resistor elétrico que teve a sua resistência elétrica triplicada?
a) Ela é triplicada.
b) Ela é duplicada.
c) Ela não muda.
d) Ela é diminuída pelo triplo.
e) Ela é diminuída pela metade.
LETRA A
A resistividade elétrica é proporcional à resistência elétrica, assim, se se triplica a resistência elétrica, a resistividade elétrica também é triplicada, mantendo o comprimento e a área de secção transversal do resistor elétrico sem variar.
-
Questão 8
Qual é a corrente elétrica que passa por um resistor de 25 mΩ inserido em uma ddp de 220 V?
a) 2,2∙10-3A
b) 4,4∙103A
c) 4,4∙10-3A
d) 8,8∙103A
e) 8,8∙10-3A
LETRA D
Calcualremos a corrente elétrica por meio da fórmula da 1ª lei de Ohm:
\(U=R\cdot i\)
\(220=25m\cdot i\)
Em que o símbolo m representa 10-3, portanto:
\(220=25\cdot10^{-3}\cdot i\)
\(i=\frac{220}{25\cdot10^{-3} }\)
\(i=8,8\cdot10^3 A\)
-
Questão 9
Calcule o comprimento de um fio de ferro que apresenta uma resistividade elétrica de 10-5Ω∙m, resistência elétrica de 4∙10-2Ω e área de secção transversal igual a 0,5 m.
a) 250 metros
b) 500 metros
c) 1000 metros
d) 1500 metros
e) 2000 metros
LETRA E
Calcularemos o comprimento do fio por meio da fórmula da 2ª lei de Ohm:
\(ρ=\frac {R\cdot A}{L}\)
\(10^{-5}=\frac{4\cdot10^{-2}\cdot0,5}{L}\)
\(L=\frac {4\cdot10^{-2}\cdot0,5} {10^{-5} }\)
\(L=2\cdot10^{-2}\cdot 10^5\)
\(L=2\cdot10^{-2+5}\)
\(L=2\cdot10^3\)
\(L=2000 m\)
-
Questão 10
Um aparelho eletrônico possui em seu circuito elétrico um resistor com determinada resistência elétrica. Quando ele é inserido em uma tomada de 110 V, acaba sendo percorrido por uma corrente elétrica de 6 μA. Com base nisso, calcule a resistência elétrica desse resistor.
a) 18,3∙104 Ω
b) 18,3∙105 Ω
c) 18,3∙106 Ω
d) 18,3∙107 Ω
e) 18,3∙108 Ω
LETRA C
Calcularemos o valor da resistência elétrica por meio da fórmula da 1ª lei de Ohm:
\(R=\frac{U} {i}\)
\(R=\frac{110} {6μ}\)
Em que o símbolo μ representa 10-6, portanto:
\(R=\frac{110} {6\cdot10^{-6} }\)
\(R≅18,3\cdot10^6 Ω\)
-
Questão 11
Um condutor com 6 metros de comprimento e 10-2 metros de área transversal apresenta uma resistência elétrica de 2,4∙10-4Ω. Com isso, determine a sua resistividade elétrica.
a) 4∙10-7Ω∙m
b) 4,5∙10-7Ω∙m
c) 5∙10-7Ω∙m
d) 5,5∙10-7Ω∙m
e) 6∙10-7Ω∙m
LETRA A
Calcularemos a resistividade elétrica por meio da fórmula da 2ª lei de Ohm:
\(ρ=\frac{R\cdot A}{L}\)
\(ρ=\frac{2,4\cdot10^{-4}\cdot10^{-2}}{6}\)
\(ρ=0,4\cdot10^{-6}\)
\(ρ=0,4\cdot10^{-6}\)
\(ρ=4\cdot10^{-1}\cdot10^{-6}\)
\(ρ=4\cdot10^{-1-6} \)
\(ρ=4\cdot10^{-7} Ω\cdot m\)
-
Questão 12
Qual(is) das alternativa(s) apresenta(m) a unidade de medida correspondente à grandeza física estudada nas leis de Ohm:
I. A resistividade elétrica é medida em [Ω∙m]-1.
II. A resistência elétrica é medida em Ohm.
III. O comprimento do condutor é medido em metros quadrados.
IV. A tensão elétrica é medida em Volts.
V. A corrente elétrica é medida em Volts.
a) Alternativas I e II
b) Alternativas III e IV
c) Alternativas I e V
d) Alternativas II e III
e) Alternativas II e IV
LETRA E
Apenas as alternativas II e IV estão corretas. Abaixo, em vermelho, está a correção das alternativas incorretas:
I. Incorreta. A resistividade elétrica é medida em [Ω∙m].
II. Correta.
III. Incorreta. O comprimento do condutor é medido em metros.
IV. Correta.
V. Incorreta. A corrente elétrica é medida em Ampère.