Exercícios sobre Mecânica
(UFPR) Um ponto em movimento circular uniforme descreve 15 voltas por segundo em uma circunferência de 8,0 cm de raio. A sua velocidade angular, o seu período e a sua velocidade linear são, respectivamente:
A) 20 rad/s, (1/15) s, 280 π cm/s
B) 30 rad/s, (1/10) s, 160 π cm/s
C) 30 π rad/s, (1/15) s, 240 π cm/s
D) 60 π rad/s, 15 s, 240 π cm/s
E) 40 π rad/s, 15 s, 200 π cm/s
Alternativa C.
Calcularemos a velocidade angular através da fórmula que a relaciona à frequência:
\(ω=2\cdot π\cdot f\)
\(ω=2\cdot π\cdot 15\)
\(ω=30 π\ rad/s\)
Depois, calcularemos o período através da fórmula que o relaciona à frequência:
\(T=\frac{1}f\)
\(T=\frac{1}{15}s\)
Por fim, calcularemos a velocidade linear através da fórmula que a relaciona à velocidade angular e ao raio:
\(v=ω\cdot r\)
\(v=30π\cdot 8\)
\(v=240π\ cm/s\)
(Fatec) Na teoria da relatividade restrita de Einstein, dois conceitos estudados referem-se ao fato de que, ao considerar um objeto propagando-se à velocidade da luz, podemos verificar
A) a dilatação do tempo e a dilatação do comprimento.
B) a contração do tempo e a dilatação do comprimento.
C) a dilatação do tempo e a contração do comprimento.
D) a dilatação do tempo sem contração do comprimento.
E) a contração do tempo sem contração do comprimento.
Alternativa C.
Na teoria da relatividade restrita de Einstein, quando um objeto está propagando-se à velocidade da luz, ele observa a dilatação do tempo e a contração do comprimento.
(Fuvest - adaptada) No rótulo de uma lata de leite em pó lê-se “valor energético: 1509 kJ por 100 g (361 kcal)”. Se toda energia armazenada em uma lata contendo 400 g de leite fosse utilizada para levantar um objeto de 10 kg, a altura máxima atingida seria de, aproximadamente: (g = 10 m/s²)
A) h = 50,37 km
B) h = 71,36 km
C) h = 61,37 km
D) h = 60,36 km
E) h = 70,36 km
Alternativa D.
Inicialmente, calcularemos o valor energético de 400 gramas de leite, através de uma regra de três simples:
\(100\ gramas — 1509\ KJ\)
\(400\ gramas — x\)
\(x\cdot 100=1509\cdot 400\)
\(x=\frac{603\ 600}{100}\)
\(x=6036\ kJ\)
\(x=6036\cdot 10^3\ J\)
Depois, calcularemos a altura máxima atingida para levantar a lata, através da fórmula da energia potencial gravitacional:
\(E_{pg}=m\cdot g\cdot h\)
\(6036\cdot 10^3=10\cdot 10\cdot h\)
\(6036\cdot 10^3=100\cdot h\)
\(h=\frac{6036\cdot 10^3}{100}\)
\(h=\frac{6036\cdot 1000}{100}\)
\(h=60\ 360\ m\)
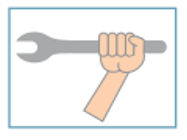
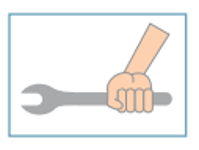
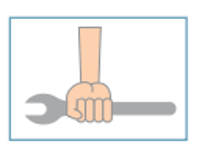
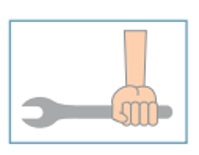
(Uerj) A figura abaixo ilustra uma ferramenta utilizada para apertar ou desapertar determinadas peças metálicas.
Para apertar uma peça, aplicando a menor intensidade de força possível, essa ferramenta deve ser segurada de acordo com o esquema indicado em:
A) 
B) 
C) 
D) 
Alternativa D.
Para apertar a peça com a menor intensidade de força possível, precisamos aplicar a força na extremidade e na vertical, já que quanto mais próximo a mão estiver do orifício direito, mais força é feita.
Qual das forças abaixo é responsável pela deformação e elongação dos corpos?
A) força elétrica.
B) força normal.
C) força elástica.
D) força peso.
E) força de atrito.
Alternativa D.
A força responsável pela deformação e elongação dos corpos é a força elástica, calculada através da lei de Hooke.
A partir dos seus conhecimentos a respeito das leis de Kepler, qual das alternativas não corresponde a uma delas?
A) lei das órbitas elípticas
B) lei das áreas
C) lei dos períodos
D) lei da ação e reação
Alternativa D.
A lei de ação e reação não é uma das leis de Kepler, mas uma das leis de Newton. Ela diz respeito ao princípio de ação e reação das forças sobre os corpos.
Determine a aceleração centrípeta de um automóvel com velocidade linear de 80 m/s que percorre uma curva com raio 5 m.
A) \(763\ m/s^2 \)
B) \(874\ m/s^2\)
C) \(982\ m/s^2\)
D) \(1125\ m/s^2\)
E) \(1280\ m/s^2\)
Alternativa E.
Calcularemos a aceleração centrípeta através da sua fórmula:
\(a_{cp}=\frac{v^2}R\)
\(a_{cp}=\frac{80^2}5\)
\(a_{cp}=\frac{6400}5\)
\(a_{cp}=1280\ m/s^2\)
Qual a força que ocorre sobre um pistão maior quando se faz uma força de 500 N sobre um pistão menor de uma prensa hidráulica, sabendo que seus raios são de 0,2 metros e 0,4 metros?
A) 200 N
B) 400 N
C) 600 N
D) 800 N
E) 1000 N
Alternativa A.
Primeiramente, calcularemos a área do pistão maior:
\(A_1=π\cdot r_1^2\)
\(A_1=π\cdot 0,2^2\)
\(A_1= 0,04π\ m^2 \)
E a área do pistão menor:
\(A_2=π\cdot r_2^2\)
\(A_2=π\cdot 0,4^2\)
\(A_2=0,16π\ m^2\)
Por fim, substituiremos os dados na fórmula do teorema de Pascal:
\(\frac{F_1}{A_1} =\frac{F_2}{A_2} \)
\(\frac{500}{0,04π}=\frac{F_2}{0,16π}\)
\(F_2=\frac{500\cdot 0,16π}{0,4π}\)
\(F_2=200\ N\)
Qual a velocidade média, em metros por segundo, de um automóvel que se desloca 151,2 km em 1 hora?
A) 12 m/s
B) 18 m/s
C) 20 m/s
D) 31 m/s
E) 42 m/s
Alternativa E.
Primeiramente, calcularemos a velocidade média através da sua fórmula:
\(v_m=\frac{∆x}{∆t}\)
\(v_m=\frac{151,2}1\)
\(v_m=150\ km/s\)
Como é pedida a velocidade média em m/s, basta dividirmos km/h por 3,6:
\(\frac{151,2\ km/h}{3,6}=42\ m/s\)
Sabendo que o peso de uma pessoa na Terra é de 800 N e em outro planeta é de 1200 N, calcule a aceleração da gravidade desse outro planeta, considerando que a aceleração da gravidade na Terra é de \(10\ m/s^2\).
A) \(1,2\ m/s^2\)
B) \(1,3\ m/s^2\)
C) \(1,4\ m/s^2\)
D) \(1,5\ m/s^2\)
E) \(1,6\ m/s^2\)
Alternativa D.
Primeiramente, calcularemos a massa da pessoa na Terra:
\(P=m\cdot g\)
\(800=m\cdot 10\)
\(m=\frac{800}{10}\)
\(m=80\ kg\)
Depois, calcularemos a aceleração da gravidade do planeta através da fórmula da força peso:
\(P=m\cdot g\)
\(1200=80\cdot g\)
\(g=\frac{1200}{800}\)
\(g=1,5\ m/s^2\)
Determine a aceleração de um carro esportivo que partiu do repouso e atingiu uma velocidade de 198 km/h em 4s.
A) \(9,63\ m/s^2\)
B) \(13,75\ m/s^2\)
C) \(18,12\ m/s^2\)
D) \(20,94\ m/s^2\)
E) \(25,86\ m/s^2 \)
Alternativa B.
Primeiramente, converteremos a aceleração do carro de km/h para m/s:
\(\frac{198\ km/h}{3,6}=55\ m/s\)
Depois, calcularemos a aceleração através da fórmula que a relaciona à velocidade e ao tempo:
\(v_f=v_i+a\cdot t\)
\(55=0+a\cdot 4\)
\(55=a\cdot 4\)
\(\frac{55}4=a\)
\(13,75\ m/s^2=a\)
Um tanque de água possui volume de \(7,0\ x\ 10^3\) litros, com 2,0 metros de comprimento e 1,0 metro de largura. Calcule a pressão hidrostática exercida pela água em seu fundo, considerando que a aceleração da gravidade é de \(10\ m/s^2\):
A) \(3,5 \cdot 10^4\ Nm^{-2}\)
B) \(2,5 \cdot 10^4\ Nm^{-2}\)
C) \(1,5 \cdot 10^4\ Nm^{-2}\)
D) \(1,0 \cdot 10^4\ Nm^{-2}\)
E) \(0,5 \cdot 10^4\ Nm^{-2}\)
Alternativa A.
Primeiramente, para convertermos o volume de litros para metros cúbicos, basta dividirmos por 1000:
\(V=\frac{7\cdot 10^3\ L}{1000}=\frac{5\cdot 10^3\ L}{10^3}=7\ m^3\)
Depois, calcularemos a altura a partir do volume, que é dado pelo produto da largura, comprimento e altura:
\(V=l\cdot c\cdot h\)
\(7=1\cdot 2\cdot h\)
\(7=2\cdot h\)
\(\frac{7}2=h\)
\(3,5=h\)
Por fim, calcularemos a pressão hidrostática exercida pela água no fundo do tanque, através da lei de Stevin:
\(p=d\cdot g\cdot h\)
Considerando a densidade da água como \(1000\ kg/m^3 \) e a gravidade como \(10\ m/s^2\), temos que:
\(p=1000\cdot 10\cdot 3,5\)
\(p=3,5\cdot 10^4\ Pa=3,5 \cdot 10^4\ Nm^{-2}\)
