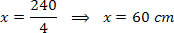Exercícios sobre momento de uma força
De acordo com o estudo sobre a estática do corpo rígido, mais precisamente sobre momento de uma força, marque a alternativa que completa a frase abaixo.
Quando um corpo extenso está sujeito à ação de forças de resultante não nula, ele pode adquirir movimento de _______, de _______ ou ______, simultaneamente.
a) translação, rotação, ambos.
b) aplicação, rotação, relação.
c) translação, relação, rotação.
d) equilíbrio, rotação, ação.
e) equilíbrio, relação, ambos.
A frase escrita de forma correta é: Quando um corpo extenso está sujeito à ação de forças de resultante não nula, ele pode adquirir movimento de translação, de rotação ou ambos, simultaneamente. Portanto, as palavras que completam a frase são: translação, rotação, ambos.
Alternativa A
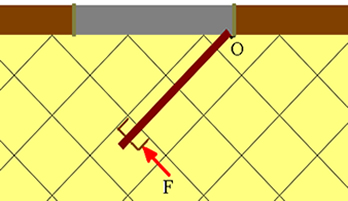
Suponha que para fechar uma porta de 0,8 metros de largura, uma pessoa aplica perpendicularmente a ela uma força de 3 N, como mostra a figura abaixo. Determine o momento dessa força em relação ao eixo O.
a) M = -3,75 N.m
b) M = -2,4 N.m
c) M = -0,27 N.m
d) M = 3,75 N.m
e) M = 2,4 N.m
Podemos ver pela figura que o momento dessa força será negativo, pois ela gira no sentido horário, portanto, temos que:
M = -F.d ⟹ M = -3 .0,8 ⟹ M = -2,4 N.m
Alternativa B
(UFV) Um rapaz de 900 N e uma garota de 450 N estão em uma gangorra. Das ilustrações abaixo, a que representa uma situação de equilíbrio é:
a)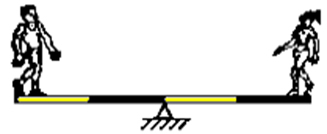
b)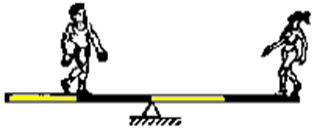
c)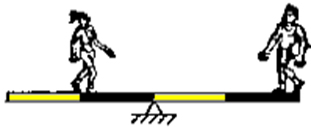
d)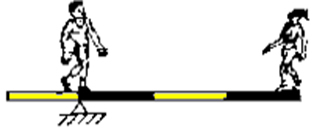
e)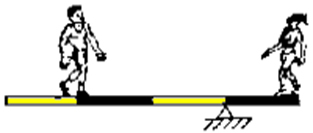
Para resolver essa situação basta igualar os momentos, isto é, o momento de força do rapaz é igual ao momento de força da moça, ambos sobre a barra, portanto, temos:
Mrapaz=Mmoça
Fr.d1=Fm.d2
Como o peso do homem é o dobro do peso da moça, ele deve estar na metade da distância do apoio.
900 . 1 = 450 .2
Alternativa B
Vejamos a figura abaixo. Na figura temos dois blocos cujas massas são, respectivamente, 4 kg e 6 kg. A fim de manter a barra em equilíbrio, determine a que distância x o ponto de apoio deve ser colocado. Suponha que inicialmente o ponto de apoio esteja a 40 cm da extremidade direita da barra.
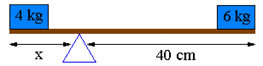
a) x = 60 cm
b) x = 20 cm
c) x = 50 cm
d) x = 30 cm
e) x = 40 cm
Para que a barra se mantenha em equilíbrio o momento do conjunto tem que ser igual a zero.
M1=M2
F1.d1=F2.d2
4 . x = 6 .40