Exercícios sobre movimento oscilatório
(Unitau) Um corpo de massa m, ligado a uma mola de constante elástica k, está animado de um movimento harmônico simples. Nos pontos em que ocorre a inversão no sentido do movimento:
A) são nulas a velocidade e a aceleração.
B) são nulas a velocidade e a energia potencial.
C) o módulo da aceleração e a energia potencial são máximos.
D) a energia cinética é máxima e a energia potencial é mínima.
E) a velocidade, em módulo, e a energia potencial são máximas.
Alternativa C
No movimento harmônico simples (MHS), uma forma de movimento oscilatório, nos pontos em que ocorre a inversão no sentido do movimento, ocorrem uma velocidade nula e, consequentemente, uma energia cinética nula. Com isso, a energia potencial é máxima, assim como a aceleração.
(UFGD) Uma oscilação harmônica é conhecida por ter força de restauração proporcional ao deslocamento. Para esse tipo de oscilação, é possível dizer que:
A) A frequência de oscilação independe do valor da força restauradora.
B) A frequência da energia total do oscilador independe do valor da força restauradora.
C) O período é o mesmo para qualquer valor da força restauradora.
D) O período depende do valor da energia mecânica do sistema.
E) A energia mecânica do sistema é constante.
Alternativa E
Nas oscilações harmônicas, não temos forças dissipativas, como a força de atrito e a força de arraste, já que a energia mecânica é conservada.
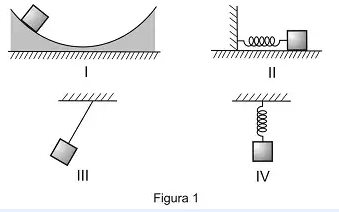
(AFA) Uma partícula de massa m pode ser colocada a oscilar em quatro experimentos diferentes, como mostra a Figura 1 abaixo.
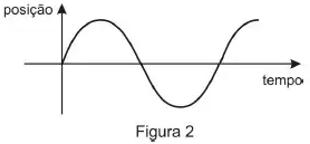
Para apenas duas dessas situações, tem-se o registro do gráfico senoidal da posição da partícula em função do tempo apresentado na Figura 2.
Considere que não existam forças dissipativas nos quatro experimentos; que, nos experimentos II e IV, as molas sejam ideais e que as massas oscilem em trajetórias perfeitamente retilíneas; que, no experimento III, o fio conectado à massa seja ideal e inextensível; e que, nos experimentos I e III, a massa descreva uma trajetória que é um arco de circunferência.
Nessas condições, os experimentos em que a partícula oscila certamente em movimento harmônico simples são, apenas:
A) I e III
B) II e III
C) III e IV
D) II e IV
Alternativa D
Esse gráfico senoidal descreve um movimento oscilatório na forma de movimento harmônico simples (MHS). Pensando nisso, analisaremos qual dos movimentos se trata de um MHS:
- O MHS é um movimento oscilatório que ocorre sobre um percurso retilíneo, o que exclui o experimento I.
- O pêndulo simples só é considerado um MHS para ângulos muito pequenos, então não podemos ter certeza se é o caso, o que exclui o experimento III.
- II e IV são sistemas massa-mola, um caso de MHS.
A função \(x\ \left(t\right)=(6)\cdot cos(3\pi\cdot t\ +\ \pi/3)\) descreve o movimento harmônico simples de um
corpo. Com base nela, quais são a constante de fase e a velocidade no instante t=5 s ?
A) \(\frac{\pi}{3};\ \frac{\pi}{3}\ rad/s\).
B) \(3\pi; \frac{\pi}{3}rad/s\).
C) \(\frac{\pi}{3}; 3\pi\ rad/s\).
D) \(3\pi; 3\pi\ rad/s\).
E) \(0;\ 0\ rad/s\).
Alternativa C
A função horária da posição do movimento oscilatório pode ser expressa pela fórmula:
\(x\left(t\right)=A\cdot\cos{(\omega\cdot t+\phi)}\)
\(x\left(t\right)=6\cdot cos\left(3\pi\cdot t\ +\frac{\pi}{3}\right)\)
Comparando-a com a equação dada no enunciado, vemos que a constante de fase (símbolo ϕ ) é \(\frac{\pi}{3},\), e a velocidade angular (símbolo ω ) é 3π rad/s .
De acordo com seus conhecimentos a respeito do movimento oscilatório, qual das alternativas é falsa?
A) O período é o tempo que levou para concluir um ciclo.
B) O período de um corpo é inversamente proporcional a sua frequência.
C) A frequência de um corpo é dada pelo número de oscilações em um intervalo de tempo.
D) A frequência pode ser medida em rpm, rotações por minuto, ou Hertz.
E) O período de um corpo é diretamente proporcional a sua frequência.
Alternativa E
O período é inversamente proporcional à frequência.
Determine a frequência de oscilação de um pêndulo que se movimenta com velocidade angular \(\frac{\pi}{2}\ rad/s\).
A) 0,25 Hz
B) 0,5 Hz
C) 1,0 Hz
D) 2,0 Hz
E) 4,0 Hz
Alternativa A
Calcularemos a frequência do movimento por meio da fórmula da velocidade angular:
\(v=2\cdot\pi\cdot f\)
\(\frac{\pi}{2}=2\cdot\pi\cdot f\)
\(f=\frac{\pi}{2}\cdot\frac{1}{2\cdot\pi}\)
\(f=\frac{1}{4}\)
\(f=0,25\ Hz\)
A função horária da posição horizontal de um corpo que descreve um movimento oscilatório é expressa abaixo em unidades do Sistema Internacional de Unidades:
\(x\left(t\right)=\cos{\left(4\pi t+\frac{\pi}{2}\right)}\)
Qual valor da amplitude e da frequência respectivamente:
A) 1 m ; 2 Hz .
B) 4 m ; 8 Hz .
C) 2 m ; 1 Hz .
D) 8 m ; 4 Hz .
E) 0 m ; 3 Hz .
Alternativa A
A função horária da posição do movimento oscilatório pode ser expressa pela fórmula:
\(x\left(t\right)=A\cdot\cos{(\omega t+\phi)}\)
Comparando esta com a equação dada no enunciado, vemos que a amplitude é 1 metro, a velocidade angular é 4π e a constante de fase é π2. Já a frequência angular calcularemos por meio da fórmula que a relaciona à velocidade angular:
\(v=2\cdot\pi\cdot f\)
\(4\cdot\pi=2\cdot\pi\cdot f\)
\(f=\frac{4\cdot\pi}{2\cdot\pi}\)
\(f=2\ Hz\)
O que acontecerá com o período de oscilação de um relógio de pêndulo que teve o comprimento do seu fio diminuído?
A) Aumentará três vezes mais rápido.
B) Diminuirá três vezes mais rápido.
C) Será nulo.
D) Aumentará
E) Diminuirá.
Alternativa E
Quando diminuimos o comprimento do fio do pêndulo, a distância que ele percorrerá será menor, ele levará menos tempo em cada oscilação e, portanto, o seu período diminuirá.
Determine a aceleração máxima de uma plataforma que oscila com uma amplitude de 0,03 m e uma frequência de 5 Hz .
Considere π = 3.
A) 14 m/s2
B) 27 m/s2
C) 39 m/s2
D) 46 m/s2
E) 58 m/s2
Alternativa B
Calcularemos a aceleração máxima por meio da sua fórmula:
\(a\left(t\right)=\omega^2\cdot x\left(t\right)\)
\(a\left(t\right)=\left(2\cdot\pi\cdot f\right)^2\cdot x\left(t\right)\)
\(a\left(t\right)=\left(2\cdot3\cdot5\right)^2\cdot0,3\)
\(a\left(t\right)=\left(30\right)^2\cdot0,3\)
\(a\left(t\right)=900\cdot0,03\)
\(a\left(t\right)=27\ m/s^2\)
Qual a frequência de oscilação de um corpo que descreve um movimento oscilatório realizando 30 oscilações por minuto?
A) 0,5 Hz
B) 1,0 Hz
C) 1,5 Hz
D) 2,0 Hz
E) 2,5 Hz
Alternativa A
Calcularemos a frequência do movimento por meio da fórmula do período:
\(T=\frac{∆t}{n}\)
Como o período pode ser calculado pelo inverso da frequência, temos:
\(\frac{1}{f}=\frac{60}{30}\)
\(\frac{1}{f}=2\ s\)
\(f=\frac{1}{2}\)
\(f=0,5\ Hz\)
Um corpo oscila com uma frequência de 200 Hz , isso quer dizer que:
A) a sua velocidade angular é nula.
B) a sua velocidade angular é de 0,005 rad/s.
C) o seu período é nulo.
D) o seu período é de 0,005 segundo.
E) a sua frequência equivale a 200 segundos.
Alternativa D
Para identicarmos a alternativa correta, calcularemos a velocidade angular por meio da sua fórmula:
\(v=2\cdot\pi\cdot f\)
\(v=2\cdot\pi\cdot200\)
\(v=400\pi\ rad/s\)
E depois, calcularemos o período por meio da fórmula que o relaciona à frequência:
\(T=\frac{1}{f}\)
\(T=\frac{1}{200}\)
\(T=0,005\ s\)
Qual(is) das alternativas apresenta(m) a unidade de medida correspondente à grandeza física estudada no movimento oscilatório:
I. A frequência é medida em Hertz.
II. O período é medido em segundo.
III. A velocidade angular é medida em metros por segundo.
IV. A amplitude é medida em radianos.
Está(ão) correta(s):
A) I, II.
B) III, IV.
C) I, IV.
D) II, III.
E) I, II e IV.
Alternativa A
I. A frequência é medida em Hertz. (Correta)
II. O período é medido em segundo. (Correta)
III. A velocidade angular é medida em metros por segundo. (Incorreta)
A velocidade angular é medida em radianos por segundo.
IV. A amplitude é medida em radianos. (Incorreta)
A amplitude é medida em metros.
