Leia conteúdos de todas as disciplinas
Exercícios sobre o plano inclinado
(PUC) Os corpos A e B de massas mA e mB, respectivamente, estão interligados por um fio que passa pela polia, conforme a figura. A polia pode girar livremente em torno de seu eixo. A massa do fio e da polia são considerados desprezíveis.
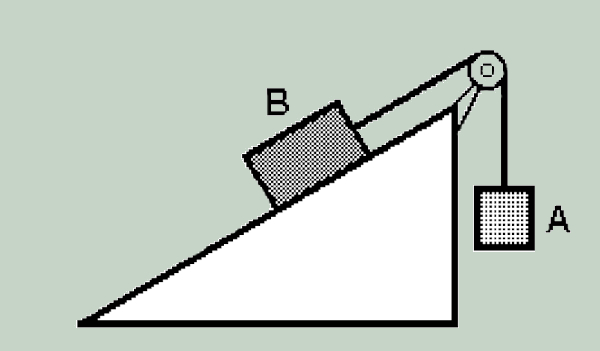
Se o sistema está em repouso, é correto afirmar:
I. Se mA = mB, necessariamente existe atrito entre o corpo B e o plano inclinado.
II. Independente de existir ou não atrito entre o plano e o corpo B, deve-se ter mA = mB.
III. Se não existir atrito entre o corpo B e o plano inclinado, necessariamente mA > mB.
IV. Se não existir atrito entre o corpo B e o plano inclinado, necessariamente mB > mA.
Está correta ou estão corretas:
A) Somente I.
B) Somente II.
C) I e III.
D) I e IV.
E) Somente III.
Alternativa D.
II. Independente de existir ou não atrito entre o plano e o corpo B, deve-se ter mA = mB. (incorreta)
Para que as massas sejam iguais, deve existir atrito entre o bloco B e a superfície.
III. Se não existir atrito entre o corpo B e o plano inclinado, necessariamente mA > mB. (incorreta)
Se não existir atrito entre o bloco B e a superfície, não necessariamente mA > mB.
(PUC) A figura 1 representa um bloco de massa m que, após ser lançado com velocidade v, sobe uma rampa de comprimento L, sem atrito, inclinada de um ângulo q.
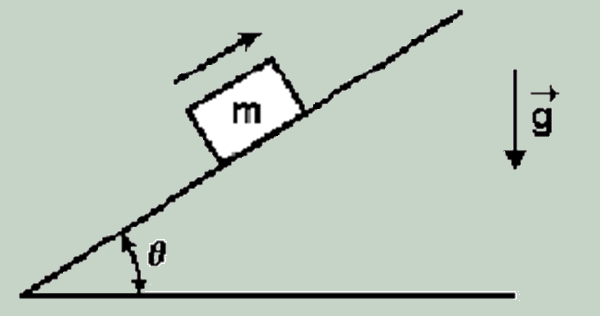
Assinale a opção que corresponde às forças que atuam no bloco enquanto ele estiver subindo a rampa.
A) 
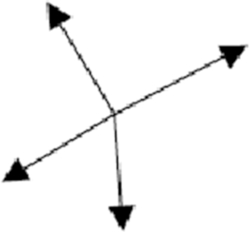
B) 
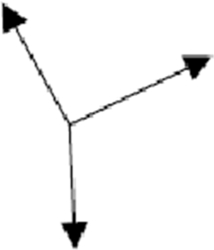
C) 
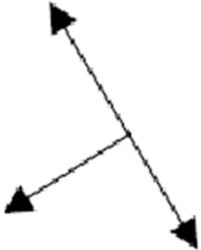
D) 
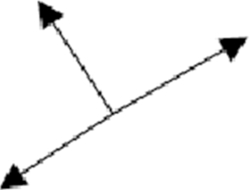
Alternativa C.
Nesse exemplo temos a força normal perpendicular à superfície e a força peso apontando para o centro da Terra, sendo decomposta em uma componente perpendicular ao bloco para a esquerda e em outra componente perpendicular ao bloco para baixo.
(UFPel) Um caminhão-tanque, após sair do posto, segue, com velocidade constante, por uma rua plana que, num dado trecho, é plana e inclinada.
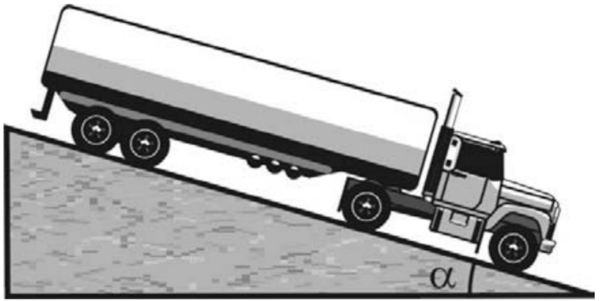
O módulo da aceleração da gravidade, no local, é g = 10 m/s2, e a massa do caminhão, 22 t, sem considerar a do combustível. É correto afirmar que o coeficiente de atrito dinâmico entre o caminhão e a rua é:
A) μ = cot α
B) μ = csc α
C) μ = sen α
D) μ = tg α
E) μ = cos α
Alternativa D.
Calcularemos o coeficiente de atrito dinâmico empregando a fórmula da força de atrito:
→fat=μ⋅→N
Isolando o coeficiente de atrito dinâmico, temos:
μ=→fat→N
A força de atrito é igual à componente horizontal da força peso e a força normal é igual à componente vertical da força peso:
μ=→Px→Py
μ=P ⋅ senθP ⋅ cosθ
μ=sen θcosθ
μ=tg θ
(Ufal - Adaptada) Uma rampa AB, inclinada de 37° em relação à horizontal, tem 12 m de comprimento e não oferece atrito para um pequeno corpo de massa 1,0 kg, abandonado, a partir do repouso no ponto A.
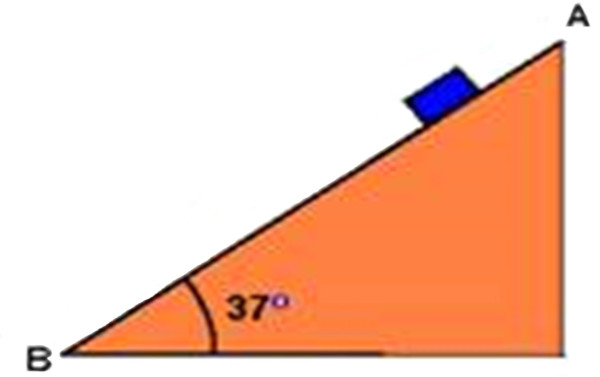
Adote g = 10m/s2, cos 37° = 0,80 e sen 37° = 0,60. Determine a força resultante sobre o corpo.
A) 5 N
B) 6 N
C) 7 N
D) 8 N
E) 9 N
Alternativa B.
Calcularemos a força resultante por meio da fórmula da segunda lei de Newton, sendo a força resultante dada pela componente horizontal da força peso, a única força responsável pelo movimento desse bloco:
FR=m⋅a
Px=m⋅a
P⋅sen 37∘=m⋅a
m⋅g⋅sen 37∘=m⋅a
1⋅10⋅0,6=1⋅a
6=1⋅a
a=6m/s2
Por fim, calcularemos a força resultante por meio da fórmula da segunda lei de Newton:
FR=m⋅a
FR=1⋅6
FR=6N
Com base nos seus conhecimentos sobre plano inclinado, responda: o plano inclinado é uma superfície obrigatoriamente
A) com ângulo de inclinação.
B) plana.
C) com atrito.
D) vertical.
E) com fio.
Alternativa A.
O plano inclinado é uma superfície obrigatoriamente com ângulo de inclinação que pode ou não ter atrito.
Em um plano inclinado de 30º com relação à horizontal, é abandonada uma bola de 2,5 kg. Desconsiderando o atrito entre o plano e o bloco, qual foi a aceleração dessa bola?
Adote g = 10 m/s2, sen 30° = 0,5 e cos 30° = 0,9.
A) 1 m/s2
B) 2 m/s2
C) 3 m/s2
D) 4 m/s2
E) 5 m/s2
Alternativa E.
Calcularemos a aceleração da bola por meio da fórmula da segunda lei de Newton, sendo a força resultante dada pela componente horizontal da força peso, a única força responsável pelo movimento desse bloco:
FR=m⋅a
Px=m⋅a
P⋅sen 30∘=m⋅a
m⋅g⋅sen 30∘=m⋅a
2,5⋅10⋅0,5=2,5⋅a
12,5=2,5⋅a
a=12,52,5
a=5m/s2
Determine o ângulo de inclinação de um plano inclinado que tem um corpo apoiado sobre ele. Considere que a força normal sobre o corpo é de 100 N e a que força peso sobre ele é de 200 N.
A) 5°
B) 15°
C) 30°
D) 60°
E) 90°
Alternativa D.
Calcularemos o ângulo de inclinado do plano por meio da fórmula que o relaciona à força normal e à força peso:
N=P⋅cosθ
100200=cosθ
0,5=cosθ
60°=θ
Quais das alternativas abaixo são casos de planos inclinados, sabendo que existem apenas dois deles:
I - Plano inclinado com atrito.
II - Plano inclinado deformável.
III - Plano inclinado resistente.
IV - Plano inclinado sem atrito.
A) Alternativas I e II.
B) Alternativas III e IV.
C) Alternativas I e III.
D) Alternativas II e IV.
E) Alternativas I e IV.
Alternativa E.
Estudamos o plano inclinado com atrito, em que consideramos a ação da força de atrito sobre os corpos, e o plano inclinado sem atrito, quando não levamos em consideração a ação da força de atrito sobre os corpos.
Calcule a força mínima para se aplicar sobre um bloco de 5 kg a fim de que ele se mova com velocidade constante na superfície de um plano inclinado sem atrito com ângulo de inclinação de 50º.
Adote g = 10 m/s2, sen 50° = 0,77 e cos 50° = 0,64.
A) 35,5 N
B) 38,5 N
C) 41,5 N
D) 44,5 N
E) 47,5 N
Alternativa B.
Calcularemos a força mínima para que o bloco se mova com velocidade constante, igualando a força resultante à força peso na direção horizontal, a força responsável pelo movimento do bloco:
FR=Px
FR=P⋅senθ
FR=m⋅g⋅sen 50°
FR=5⋅10⋅0,77
FR=38,5N
Qual força não atua sobre uma pessoa que está segurando o seu cachorro por uma coleira, que não deforma, em uma superfície áspera?
A) Força peso.
B) Força normal.
C) Força de atrito.
D) Força elástica.
E) Força de tração.
Alternativa D.
Nessa situação, como a coleira não é feita de um material deformável, então não temos força elástica.
Calcule a força de atrito sobre um corpo de 10 kg que se move em um plano inclinado de 30º com a horizontal.
Adote g = 10 m/s2, μc = 0,2 , sen 30° = 0,5 e cos 30° = 0,9.
A) 12 N
B) 14 N
C) 16 N
D) 18 N
E) 20 N
Alternativa D.
Primeiramente, calcularemos a força normal por meio da sua igualdade com a componente vertical da força peso, que mantém as duas em equilíbrio:
→N=→Py
→N=→Py
→N=P⋅cosθ
→N=m⋅g⋅cos30∘
→N=10⋅10⋅0,9
→N=90N
Por fim, calcularemos a força de atrito por meio da sua fórmula:
→fat=μ⋅→N
→fat=0,2⋅90
→fat=18N
Quais proposições apresentam a unidade de medida correspondente às grandezas físicas estudadas no plano inclinado?
I. A força peso é medida em Newton.
II. A força normal é medida em Newton.
III. A força de atrito é medida em Joule.
IV. A massa é medida em quilogramas quadrados.
V. A aceleração da gravidade é medida em metros por segundo.
A) Alternativas I e II.
B) Alternativas III e IV.
C) Alternativas I e V.
D) Alternativas II e III.
E) Alternativas II e IV.
Alternativa A.
III. A força de atrito é medida em Joule. (incorreta)
A força peso é medida em Newton.
IV. A massa é medida em quilogramas quadrados. (incorreta)
A massa é medida em quilogramas.
V. A aceleração da gravidade é medida em metros por segundo. (incorreta)
A aceleração da gravidade é medida em metros por segundo ao quadrado.
Ferramentas
