Home
Exercícios de Física
Exercícios sobre resistores

Exercícios sobre resistores

Teste seus conhecimentos por meio desta lista de exercícios sobre resistores, dispositivos elétricos que podem ser associados em série, em paralelo ou de forma mista. Publicado por: Pâmella Raphaella Melo

Imprimir

Questão 1

(Vunesp) Num circuito elétrico, dois resistores, cujas resistências são R1 e R2, com R1 > R2 , estão ligados em série. Chamando de i1 e i2 as correntes que os atravessam e de V1 e V2 as tensões a que estão submetidos, respectivamente, pode-se afirmar que:

A) i1 = i2 e V1 = V2

B) i1 = i2 e V1 > V2

C) i1 > i2 e V1 = V2

D) i1 > i2 e V1 < V2

E) i1 < i2 e V1 > V2

Ver resposta

Resposta

Alternativa B

Quando os resistores estão associados em série, as correntes elétricas que os atravessam são todas iguais e a ddp é maior no resistor que tem maior resistência elétrica.

Questão 2

(PUC) Três resistores idênticos de R=30Ω estão ligados em paralelo com uma bateria de 12V. Pode-se afirmar que a resistência equivalente do circuito é:

A) R_eq = 10 Ω, e a corrente é de 1,2 A .

B) R_eq = 20 Ω, e a corrente é de 0,6 A .

C) R_eq = 30 Ω, e a corrente é de 0,4 A .

D) R_eq = 40 Ω, e a corrente é de 0,3 A .

E) R_eq = 60 Ω, e a corrente é de 0,2 A .

Ver resposta

Resposta

Alternativa A

Primeiramente, calcularemos a resistência equivalente dos resistores associados em paralelo por meio da sua fórmula:

$R_{eq} = \frac{R}{n}$

$R_{eq} = \frac{30}{3}$

$R_{eq} = 10 \, \Omega$

Por fim, calcularemos a corrente elétrica por meio da fórmula da primeira lei de Ohm:

$U=R \cdot i$

$12=10 \cdot i$

$i= \frac {12}{10}$

$i=1,2 A$

Questão 3

(Selecon) Dispõe-se de três resistores de resistência 300 ohms cada um. Para se obter uma resistência de 450 ohms, utilizando-se os três resistores, como devemos associá-los?

A) Dois em paralelo, ligados em série com o terceiro.

B) Os três em paralelo.

C) Dois em série, ligados em paralelo com o terceiro.

D) Os três em série.

E) n.d.a.

Ver resposta

Resposta

Alternativa A

Primeiramente, precisamos associar dois resistores em paralelo e calcular a resistência equivalente entre eles por meio da sua fórmula:

$\frac{1}{R_{eq}} = \frac{1}{R_{1}} + \frac{1}{R_{2}}$

$R_{eq} = \frac{R_{1} \cdot R_{2}}{R_{1} + R_{2}}$

$R_{eq} = \frac{300 \cdot 300}{300 + 300}$

$R_{eq} = \frac{90000}{600}$

$R_{eq}=150 Ω$

Depois, precisamos associar os resistores em série, assim, obtemos a resistência equivalente calculando-a por meio da sua fórmula:

$R_{eq}=R_1+R_2$

$R_{eq} = 150 + 300$

$R_{eq}=450 Ω$

Questão 4

(Unifesp - Adaptada) A linha de transmissão que leva energia elétrica da caixa de relógio até uma residência consiste de dois fios de cobre com 10,0m de comprimento e secção reta com área 4,0mm² cada um. Considerando que a resistividade elétrica do cobre é $ρ = 1,6 \cdot 10^{-8} Ω \cdot m$ , calcule a resistência elétrica r de cada fio desse trecho do circuito.

A) 0,01 Ω

B) 0,02 Ω

C) 0,03 Ω

D) 0,04 Ω

E) 0,05 Ω

Ver resposta

Resposta

Alternativa D

Primeiramente, converteremos, de milimetros quadrados para metros quadrados, a área de seção reta:

$4,0 {\,}\text{mm}^2 = 4 \cdot 10^{-6}\, \text{m}^2$

Por fim, calcularemos a resistência elétrica por meio da fórmula da segunda lei de Ohm:

$R =\rho \cdot \frac{L}{A}$

$R = 1{,}6 \cdot 10^{-8} \cdot \frac{10}{4 \cdot 10^{-6}}$

$R = \frac{16 \cdot 10^{-8}}{4 \cdot 10^{-6}}$

$R=4 \cdot 10^{-8+6}$

$R=4 \cdot 10^{-2}$

$R=0,04 Ω$

Questão 5

Dois resistores associados em série de resistência elétrica 2 Ω e 4 Ω são conectados a uma tomada de 120 V. Sabendo disso, qual é a corrente elétrica que percorre esses resistores?

A) 0A

B) 10A

C) 20A

D) 30A

E) 40A

Ver resposta

Resposta

Alternativa C

Primeiramente, calcularemos a resistência elétrica equivalente da associação de resistores em série por meio da sua fórmula:

$R_{eq}=R_1+R_2$

$R_{eq}=2+4$

$R_{eq}=6Ω$

Por fim, calcularemos a corrente elétrica que percorre esses resistores por meio da fórmula da primeira lei de Ohm:

$U=R \cdot i$

$120=6 \cdot i$

$i= \frac {120}{6}$

$i=20 A$

Questão 6

A associação de resistores em paralelo apresenta diversas propriedades. Com base nisso, analise as afirmativas abaixo:

I. Mesma corrente elétrica atravessando os resistores.

II. Diferentes valores de corrente elétrica atravessando os resistores.

III. Mesma tensão elétrica nos terminais de cada resistor.

IV. Diferentes valores de tensão elétrica nos terminais de cada resistor.

Quais alternativas estão corretas?

A) I e II

B) I e IV

C) II e IV

D) I e III

E) II e III

Ver resposta

Resposta

Alternativa E

Quando os resistores estão associados em paralelo, a tensão elétrica tem o mesmo valor em todos os seus terminais e a corrente elétrica tem diferente valor para cada resistor.

Questão 7

Um resistor de resistência elétrica 4 Ω é associado paralelamente com outro resistor de resistência elétrica R₂. Sabendo que a resistência equivalente dessa associação dá 2,4 Ω, determine a resistência elétrica R₂.

A) 4 Ω

B) 6 Ω

C) 8 Ω

D) 10 Ω

E) 12 Ω

Ver resposta

Resposta

Alternativa B

Calcularemos a resistência elétrica do segundo resistor associado em paralelo por meio da sua fórmula:

$R_{eq} = \frac{R_{1} \cdot R_{2}}{R_{1} + R_{2}}$

$2{,}4 = \frac{4 \cdot R_{2}}{4 + R_{2}}$

$2{,}4 \cdot (4 + R_{2}) = 4 \cdot R_{2}$

$9{,}6 + 2{,}4 \cdot R_{2} = 4 \cdot R_{2}$

$9{,}6 = 4 \cdot R_{2} - 2{,}4 \cdot R_{2}$

$9,6=1,6 \cdot R_2$

$R_{2} = \frac{9{,}6}{1{,}6}$

$R_2=6 Ω$

Questão 8

Um resistor de 0,2 m de comprimento e 10^-2 m² de área transversal tem uma resistividade elétrica de 0,5 ∙ 10^-2Ω ∙ m. Com base nessas informações, calcule a sua resistência elétrica.

A) 0,02 Ω

B) 0,05 Ω

C) 0,10 Ω

D) 0,12 Ω

E) 0,20 Ω

Ver resposta

Resposta

Alternativa C

Calcularemos a resistência elétrica por meio da fórmula da segunda lei de Ohm:

$R = \frac{\rho \cdot L}{A}$

$R = \frac{0{,}5 \cdot 10^{-2} \cdot 0{,}2}{10^{-2}}$

$R = 0{,}1 \cdot 10^{-2} \cdot 10^{2}$

$R=0,1 \cdot 10^{-2+2}$

$R=0,1 \cdot 1$

$R=0,10 Ω$

Questão 9

Determine a resistência equivalente em um circuito elétrico em que estão associados em série cinco resistores elétricos, de resistências elétricas 1 Ω, 3 Ω, 5 Ω, 7 Ω e 9 Ω.

A) 10 Ω

B) 15 Ω

C) 20 Ω

D) 25 Ω

E) 30 Ω

Ver resposta

Resposta

Alternativa D

Calcularemos a resistência elétrica equivalente nessa associação de resistores em série por meio da sua fórmula:

$R_{eq}=R_1+R_2+R_3+R_4+R_5$

$R_{eq}=1+3+5+7+9$

$R_{eq}=25 Ω$

Questão 10

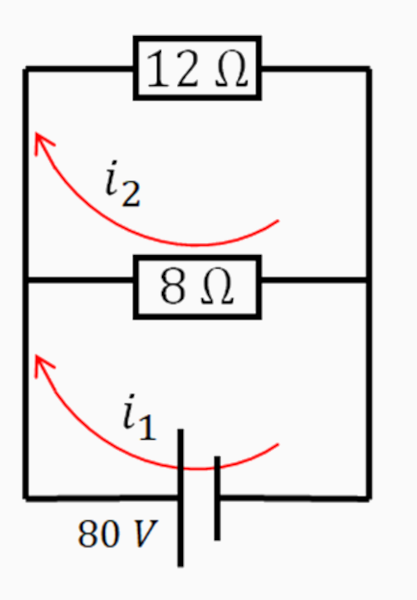
Calcule a corrente elétrica em cada resistor da associação abaixo:

Associação de resistores em paralelo em uma questão sobre resistores.

A) 10 A e $\frac {20}{3}$ A

B) 12 A e $\frac {10}{6}$ A

C) 14 A e $\frac {4}{3}$ A

D) 16 A e 2 A

E) 18 A e 8 A

Ver resposta

Resposta

Alternativa A

A ddp é a mesma em cada resistor em uma associação em paralelo, mas a corrente elétrica tem valores diferentes, então ela será calculada por meio da fórmula da primeira lei de Ohm:

$U=R_1 \cdot i_1$

$80=8 \cdot i_1$

$i_1= \frac {80}{8}$

$i_1=10 A$

Já a corrente elétrica no resistor 2 é:

$U=R_2 \cdot i_2$

$80=12 \cdot i_2$

$i_2= \frac {80}{12}$

$i_{2} = \frac{20}{3} \, \text{A}$

Questão 11

Sabendo que três resistores, com resistências elétricas de 0,5 Ω, 1 Ω e 2 Ω, estão ligados em paralelo em um circuito elétrico, calcule a resistência equivalente.

A) 0,17 Ω

B) 0,29 Ω

C) 0,36 Ω

D) 0,48 Ω

E) 0,50 Ω

Ver resposta

Resposta

Alternativa B

Calcularemos a resistência elétrica equivalente dos resistores associados em paralelo por meio da sua fórmula:

$\frac{1}{R_{eq}} = \frac{1}{R_{1}} + \frac{1}{R_{2}} + \frac{1}{R_{3}}$

$\frac{1}{R_{eq}} = \frac{1}{0{,}5} + \frac{1}{1} + \frac{1}{2}$

$\frac{1}{R_{eq}} = 2 + 1 + 0{,}5$

$\frac{1}{R_{eq}} = 3{,}5$

$R_{eq} = \frac{1}{3{,}5}$

$R_{eq} \cong 0{,}29 \, \Omega$

Questão 12

Um resistor mantém a sua resistividade elétrica, mas tem seu comprimento triplicado e sua área duplicada, então o valor da sua resistência elétrica nova é:

A) 1 ∙ R

B) 2 ∙ R

C) 3 ∙ R

D) 2,5 ∙ R

E) 1,5 ∙ R

Ver resposta

Resposta

Alternativa E

A resistência elétrica do resistor, antes, foi dada pela expressão obtida da fórmula da segunda lei de Ohm:

$R = \frac{\rho \cdot L}{A}$

A nova resistência elétrica do resistor foi dada pela expressão obtida da fórmula da segunda lei de Ohm:

$R' = \frac{\rho \cdot 3L}{2A}$