Exercícios sobre roldanas ou polias
(IFPE) Considere a máquina de Atwood a seguir, onde a polia e o fio são ideais e não há qualquer atrito. Considerando que as massas de A e B são, respectivamente, 2M e 3M, e desprezando a resistência do ar, qual a aceleração do sistema? (Use \(g=10\ m/s^2\))
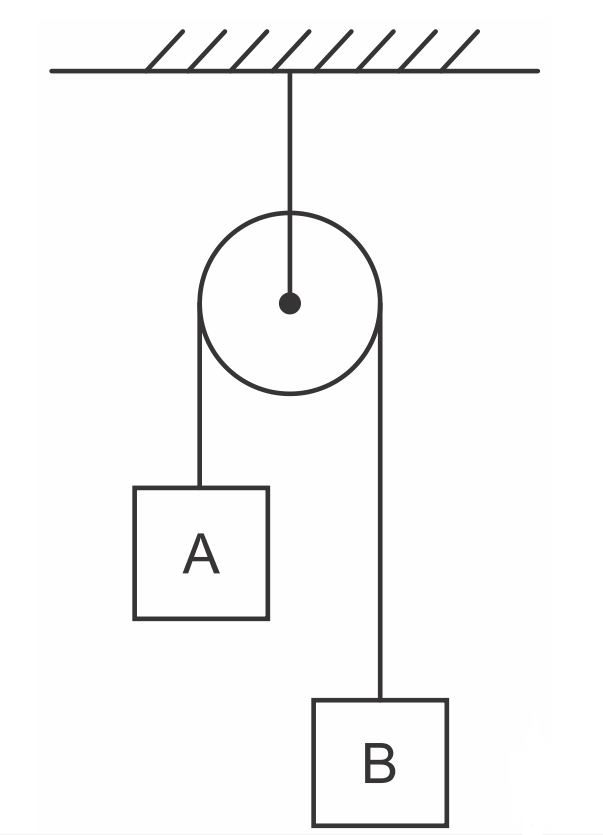
A) 5 m/s2
B) 3 m/s2
C) 2 m/s2
D) 10 m/s2
E) 20 m/s2
Alternativa C
Nesse sistema de blocos contendo uma roldana fixa, temos aceleração, assim, é necessário analisarmos o deslocamento do sistema. Como o bloco B possui massa maior do que a do bloco A, o sistema se desloca para a direita. Desse modo, no bloco B, a força peso é maior do que a força tração, e no bloco A, a força tração é maior do que a força peso.
Em razão disso, em vez de usarmos a fórmula padrão da roldana fixa, usaremos a fórmula da segunda lei de Newton para calcularmos a aceleração.
\(F_R=m\cdot a\)
Em B:
\(F_R=m_B\cdot a\)
\(P_B-T=m_B\cdot a\)
\(\left(m_B\cdot g\right)-T=m_B\cdot a\)
Em A:
\(F_R=m_A\cdot a\)
\(T-P_A=m_A\cdot a\)
\(T-\left(m_A\cdot g\right)=m_A\cdot a\)
Resultando nas equações:
\( \begin{cases} \left(m_B\cdot g\right)-T=m_B\cdot a & \quad \\ T-\left(m_A\cdot g\right)=m_A\cdot a & \end{cases}\)
Somando as equações, obtemos:
\(\left(m_B\cdot g\right)-\left(m_A\cdot g\right)=m_B\cdot a+m_A\cdot a\)
\(g\cdot\left(m_B-m_A\right)=a\cdot(m_B+m_A)\)
\(a=\frac{g\cdot\left(m_B-m_A\right)}{(m_B+m_A)}\)
\(a=\frac{10\cdot\left(3M-2M\right)}{(3M+2M)}\)
\(a=\frac{10\cdot1M}{5M}\)
\(a=\frac{10\cdot1}{5}\)
\(a=2\ m/s^2\)
(Acafe) Um homem queria derrubar uma árvore que estava inclinada e oferecia perigo de cair em cima de sua casa. Para isso, com a ajuda de um amigo, preparou um sistema de roldanas preso a outra árvore para segurar a árvore que seria derrubada, a fim de puxá-la para o lado oposto de sua suposta queda, conforme figura.
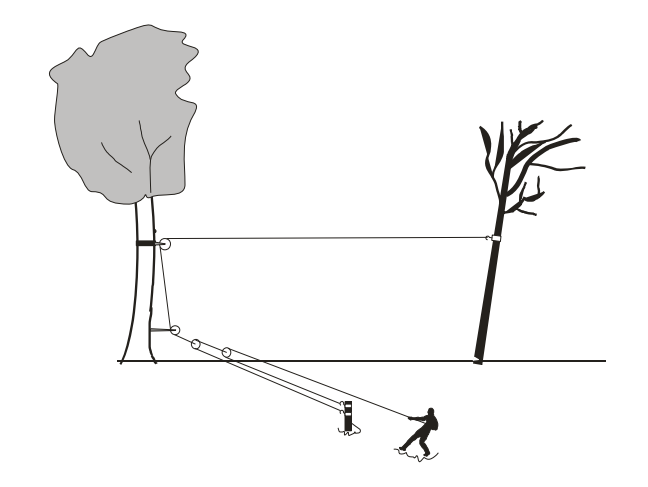
Sabendo que, para segurar a árvore em sua posição, o homem fez uma força de 1000 N sobre a corda. A força aplicada pela corda na árvore que seria derrubada é:
A) 2000 N
B) 1000 N
C) 500 N
D) 4000 N
Alternativa D
Calcularemos a força aplicada pela corda na árvore por meio da fórmula da roldana móvel:
\(F=\frac{P}{2^n}\)
\(1000=\frac{P}{2^2}\)
\(1000=\frac{P}{4}\)
\(P=1000\cdot4\)
\(P=4000\ N\)
(PUC) Analise a situação descrita.
Um geólogo, em atividade no campo, planeja arrastar um grande tronco petrificado com auxílio de um cabo de aço e de uma roldana. Ele tem duas opções de montagem da roldana, conforme as ilustrações a seguir, nas quais as forças F eT não estão representadas em escala.
Montagem 1: A roldana está fixada numa árvore; e o cabo de aço, no tronco petrificado.
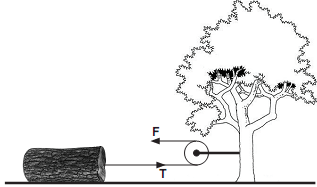
Montagem 2: A roldana está fixada no tronco petrificado; e o cabo de aço, na árvore.
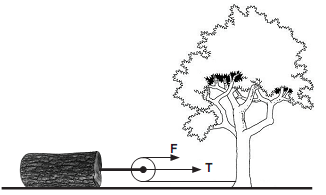
Considerando que, em ambas as montagens, a força aplicada na extremidade livre do cabo tem módulo F, o módulo da força T que traciona o bloco será igual a
A) F, em qualquer das montagens.
B) F/2, na montagem 1.
C) 2F, na montagem 1.
D) 2F, na montagem 2.
E) 3F, na montagem 2.
Alternativa D
Na montagem 1, a intensidade da força tração transferida ao tronco é equivalente à da força aplicada sobre a extremidade do fio, já que estão no mesmo cabo, portanto T = F.
Já na montagem 2, temos uma força F em cada lado da polia, então a intensidade da força tração é o dobro de F, portanto T = 2F.
(Uerj) A figura abaixo representa um sistema composto por uma roldana com eixo fixo e três roldanas móveis, no qual um corpo R é mantido em equilíbrio pela aplicação de uma força F de uma determinada intensidade.
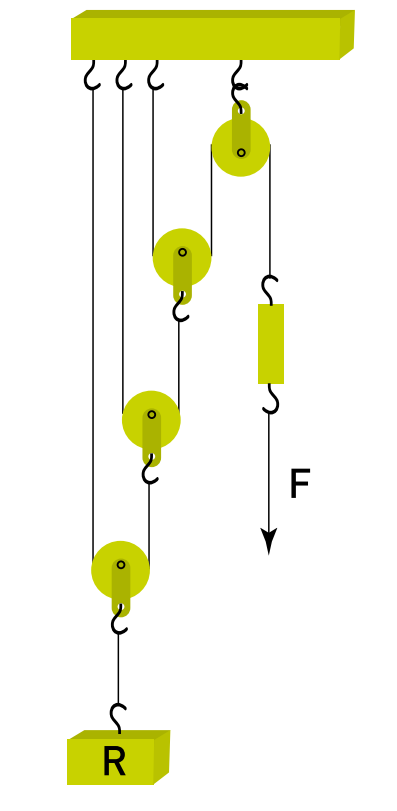
Considere um sistema análogo, com maior número de roldanas móveis e intensidade de F inferior a 0,1% do peso de R. O menor número possível de roldanas móveis para manter esse novo sistema em equilíbrio deverá ser igual a:
A) 8
B) 9
C) 10
D) 11
Alternativa C
Como temos uma associação de roldanas, calcularemos o menor número possível de roldanas móveis por meio da fórmula da associação de roldanas móveis:
\(F=\frac{P}{2^n}\)
Considerando que F é menor que 0,1%∙P , então:
\(0,1\%\cdot P>\frac{P}{2^n}\)
\(\frac{0,1}{100}\cdot P>\frac{P}{2^n}\)
\(0,001>\frac{1}{2^n}\)
\(2^n>\frac{1}{0,001}\)
\(2^n>1000\)
Assim, o número mínimo de roldanas precisa ser 10, já que 210 = 1024.
De acordo com seus estudos a respeito das roldanas ou polias, qual das alternativas abaixo corresponde a tipos de roldanas:
I. Móveis
II. Fixas
III. Paralelas
Está(ão) corretas:
A) I
B) II
C) III
D) I e II
E) II e III
Alternativa D
As roldanas ou polias podem ser fixas, quando apresentam um eixo fixo numa superfície, ou móveis, quando não apresentam um eixo fixo, sendo capazes de se moverem.
Determine a força necessária para levantar um bloco de 50 kg, considerando que ele está associado a uma roldana fixa. Considere a aceleração da gravidade como 10 m/s2 .
A) 100 N
B) 200 N
C) 300 N
D) 400 N
E) 500 N
Alternativa E
No caso de roldanas fixas, calcularemos a força necessária para deslocar o bloco, igualando-a à força peso no bloco:
\(F=P\)
\(F=m\cdot g\)
\(F=50\cdot10\)
\(F=500\ N\)
Calcule a força necessária para puxar um automóvel de 1200 kg que está associado a cinco roldanas móveis presas a uma roldana fixa. Considere a aceleração da gravidade como 10 m/s2 .
A) 375 N
B) 750 N
C) 1120 N
D) 1500 N
E) 3000 N
Alternativa A
A roldana fixa não interfere no cálculo, já que a força necessária para puxar o automóvel é igual à força peso. Calcularemos a força necessária para puxar o automóvel por meio da fórmula da associação de roldanas móveis:
\(F=\frac{P}{2^n}\)
\(F=\frac{m\cdot g}{2^n}\)
\(F=\frac{1200\cdot10}{2^5}\)
\(F=\frac{12.000}{2^5}\)
\(F=\frac{12.000}{32}\)
\(F=375\ N\)
Dentre as alternativas abaixo, qual delas não corresponde a um uso das roldanas:
A) elevadores
B) cabo de guerra
C) poços artesianos
D) guindastes
E) varais
Alternativa B
As roldanas são usadas nos elevadores, poços artesianos, guindastes e varais, mas não nos cabos de guerra — uma brincadeira composta por dois grupos de pessoas puxando uma corda sem o uso de roldanas ou polias.
Uma caixa de massa M é levantada por um guindaste contendo uma roldana fixa. Sabendo que o guindaste faz uma força de 2000 N para levantar essa caixa, calcule a massa dela. Considere a aceleração da gravidade como 10 m/s2 .
A) 200 kg
B) 250 kg
C) 300 kg
D) 350 kg
E) 400 kg
Alternativa A
No caso de roldanas fixas, calcularemos a massa da caixa pela igualdade entre a força necessária para levantá-la e a força peso sobre ela:
\(F=P\)
\(F=m\cdot g\)
\(2000=M\cdot10\)
\(M=\frac{2000}{10}\)
\(M=200\ kg\)
Calcule a força necessária para puxar um haltere de 150 kg, conectado a uma associação de roldanas contendo apenas uma roldana móvel. Considere a aceleração da gravidade como 10 m/s2.
A) 360 N
B) 750 N
C) 1120 N
D) 1500 N
E) 3000 N
Alternativa B
Como temos uma associação de roldanas, calcularemos a força necessária para puxar um haltere por meio da fórmula da associação de roldanas móveis:
\(F=\frac{P}{2^n}\)
\(F=\frac{m\cdot g}{2^n}\)
\(F=\frac{150\cdot10}{2^1}\)
\(F=\frac{1500}{2}\)
\(F=750\ N\)
As roldanas ou polias funcionam com base em três princípios físicos. Pensando nisso, quais alternativas correspondem a esses princípios?
I. Princípio da inércia
II. Princípio de Fermat
III. Princípio fundamental da dinâmica
IV. Princípio de Arquimedes
V. Princípio da ação e reação
Está(ão) correta(s):
A) I, II e III.
B) I, IV e V.
C) II, III e IV.
D) I, III e V.
E) II, IV e V.
Alternativa D
As roldanas ou polias funcionam com base nas três leis de Newton, que são: o princípio da inércia, o princípio fundamental da dinâmica, e o princípio da ação e reação.
Analise as alternativas abaixo referentes às unidades de medida estudadas em roldanas ou polias:
I. A força é medida em Newton por metro.
II. A força peso é medida em Newton por metro.
III. A massa é medida em quilogramas.
IV. A aceleração da gravidade é medida em metros por segundo ao quadrado.
V. O número de roldanas não possui unidade de medida.
Está(ão) correta(s):
A) I, II e III.
B) I, IV e V.
C) II, III e IV.
D) I, II e V.
E) III, IV e V.
Alternativa E
I. A força é medida em Newton por metro. (incorreta)
A força é medida em Newton.
II. A força peso é medida em Newton por metro. (incorreta)
A força peso é medida em Newton.
III. A massa é medida em quilogramas. (correta)
IV. A aceleração da gravidade é medida em metros por segundo ao quadrado. (correta)
V. O número de roldanas não possui unidade de medida. (correta)
