Leia conteúdos de todas as disciplinas
Exercícios sobre calor e sobre temperatura
(Uerj) Observe na tabela os valores das temperaturas dos pontos críticos de fusão e de ebulição, respectivamente, do gelo e da água, à pressão de 1 atm, nas escalas Celsius e Kelvin.
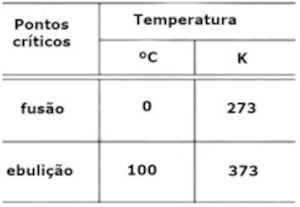
Considere que, no intervalo de temperatura entre os pontos críticos do gelo e da água, o mercúrio em um termômetro apresenta uma dilatação linear. Nesse termômetro, o valor na escala Celsius correspondente à temperatura de 313 K é igual a:
A) 20
B) 30
C) 40
D) 60
Alternativa C.
Transformaremos a temperatura na escala Kelvin para a escala Celsius empregando da fórmula:
TC=TK−273TC=313−273TC=40℃
(Uerj - Adaptada) Em um laboratório, um corpo com massa de 30g inicialmente em sua temperatura de fusão, é aquecido durante 140 s por uma fonte térmica de potência constante igual a 15 cal/s. Com o aquecimento, o corpo passa completamente do estado sólido para o estado líquido, mantendo sua temperatura constante.
Admitindo que toda a energia liberada pela fonte térmica seja integralmente absorvida pelo corpo, calcule, em cal/g o seu calor latente de fusão.
A) 60 cal/g
B) 70 cal/g
C) 80 cal/g
D) 90 cal/g
E) 100 cal/g
Alternativa B.
Primeiramente, calcularemos a quantidade de calor empregando a fórmula que a relaciona à potência térmica e ao tempo:
Q=Pott⋅ΔtQ=15⋅140Q=2100cal
Por fim, calcularemos o calor latente de fusão empregando a sua fórmula:
Q=m⋅L2100=30⋅LL=210030L=70cal/g
(IME - Adaptada) Um vidro plano, com coeficiente de condutibilidade térmica 0,00183 cal/s·cm·°C , tem uma área de 1000 cm2 e espessura de 3,66 mm . Sendo o fluxo de calor por condução através do vidro de 2000 calorias por segundo, calcule a diferença de temperatura entre suas faces.
A) 0,4 °C
B) 400 °C
C) 4000 °C
D) 40 °C
E) 4 °C
Alternativa B.
Primeiramente, transformaremos a espessura de milímetros para centímetros:
3,66 mm = 0,366 cm
Por fim, calcularemos o fluxo de calor empregando a sua fórmula:
ϕ=k⋅A⋅ΔTl2000=0,00183 ⋅ 1000 ⋅ ΔT0,3662000=1,83 ⋅ ΔT0,3662000=5⋅ΔTΔT=20005ΔT=400°C
(Uerj - Adaptada) No mapa abaixo, está representada a variação média da temperatura dos oceanos em um determinado mês do ano. Ao lado, encontra-se a escala, em graus Celsius, utilizada para a elaboração do mapa.
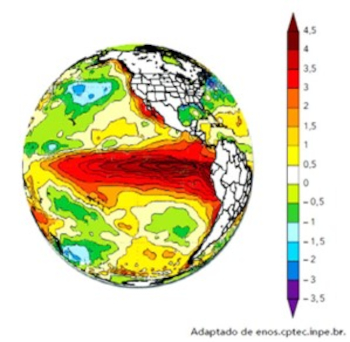
Determine, em graus Kelvin, o módulo da variação entre a maior e a menor temperatura da escala apresentada.
A) 6 K
B) 7 K
C) 8 K
D) 9 K
E) 10 K
Alternativa C.
Calcularemos a variação da temperatura na escala Celsius entre a maior temperatura e a menor temperatura:
ΔTc=4,5−(−3,5)ΔTc=8°C
A variação da temperatura na escala Celsius é igual à variação da temperatura na escala Kelvin, ou seja, de 8 K.
Ao aquecer um recipiente com 500 g de água, a sua temperatura varia de 50 °C a 80 °C. Sabendo que o calor específico da água é de 1 cal/g·°C, determine a quantidade de calor recebido.
A) 15.000 cal
B) 20.000 cal
C) 25.000 cal
D) 30.000 cal
E) 35.000 cal
Alternativa A.
Calcularemos a quantidade de calor empregando a fórmula do calor sensível:
Q=m⋅c⋅ΔTQ=m⋅c⋅(Tf−Ti)Q=500⋅1⋅(80−50)Q=500⋅1⋅(30)Q=15.000cal
Qual é a variação de comprimento de um fio metálico, de coeficiente linear igual a 0,0004 °C-1 , que sofreu uma variação de temperatura de 500°C , sabendo que seu comprimento inicial era de 1000 m ?
A) 25 m
B) 50 m
C) 100 m
D) 150 m
E) 200 m
Alternativa E.
Calcularemos a variação de comprimento do fio empregando a fórmula da dilatação linear:
ΔL=LO⋅α⋅ΔTΔL=1000⋅0,0004⋅500ΔL=200m
Um estudante de intercâmbio chegou aos Estados Unidos da América e verificou que a temperatura naquele dia era de 100 ºF, essa temperatura, em Celsius, é igual a:
A) 7,1 ℃
B) 18,9 ℃
C) 26,4 ℃
D) 37,8 ℃
E) 41,5 ℃
Alternativa D.
Transformaremos a temperatura na escala Fahrenheit para a escala Celsius empregando a sua fórmula:
TC5=TF−329TC5=100−329TC5=689TC=5⋅689TC≅37,8∘C
Qual deve ser a quantidade de calor recebido por um líquido de 250g que não variou sua temperatura, sabendo que seu calor latente é de 45 cal/g?
A) 7435 cal
B) 8712 cal
C) 9654 cal
D) 10.370 cal
E) 11.250 cal
Alternativa E.
Calcularemos a quantidade de calor empregando da fórmula do calor latente:
Q=m⋅LQ=250⋅45Q=11.250cal
Uma barra de 2 kg de determinado metal tem um calor específico de 0,08 cal/g·°C. Com base nessas informações, qual é a sua capacidade térmica?
A) 160 cal/°C
B) 200 cal/°C
C) 240 cal/°C
D) 280 cal/°C
E) 320 cal/°C
Alternativa A.
Primeiramente, transformaremos a massa de quilogramas para gramas:
2 kg = 2000 g
Por fim, calcularemos a capacidade térmica empregando a fórmula que a relaciona à massa e ao calor específico:
C=c⋅mC=0,08⋅2000C=160cal/°C
Transforme a temperatura 373 K para a escala Fahrenheit.
A) 70 ℉
B) 83 ℉
C) 96 ℉
D) 185 ℉
E) 212 ℉
Alternativa E.
Transformaremos a temperatura na escala Kelvin para a escala Fahrenheit empregando a sua fórmula:
TF−329=TK−2735TF−329=373−2735TF−329=1005TF−329=20TF−32=20⋅9TF−32=180TF=180+32TF=212∘F
Ao variar a temperatura de uma chapa metálica de aço, de coeficiente linear de 1∙10-5 °C-1 , de 60 ºC para 200 ºC, houve sua dilatação superficial. Sabendo que a sua área inicial era de 50 m2 , qual foi a variação de sua área dilatada?
A) 0,08 m2
B) 0,10 m2
C) 0,12 m2
D) 0,14 m2
E) 0,16 m2
Alternativa D.
Calcularemos a variação de área dilatada empregando a fórmula da dilatação superficial:
ΔA=AO⋅β⋅ΔTΔA=AO⋅2⋅α⋅ΔTΔA=AO⋅2⋅α⋅(Tf−Ti)ΔA=50⋅2⋅1⋅10−5⋅(200−60)ΔA=50⋅2⋅1⋅10−5⋅140ΔA=50⋅2⋅0,00001⋅140ΔA=0,14m2
Calcule o calor específico de um copo de massa 800 g que recebeu 1000 cal quando sua temperatura variou de 25 °C a 100 °C.
A) 0,015 cal/g∙°C
B) 0,016 cal/g∙°C
C) 0,017 cal/g∙°C
D) 0,018 cal/g∙°C
E) 0,019 cal/g∙°C
Alternativa B.
Calcularemos o calor específico empregando a fórmula que o relaciona ao calor, à massa e à temperatura:
c=Qm⋅ΔTc=Qm⋅(Tf−Ti)c=1000800⋅(100−25)c=1000800⋅75c=100060000c≅0,016cal/g⋅∘C
Assista às nossas videoaulas
Ferramentas
