Exercícios sobre teoria da relatividade
Para responder a estes exercícios sobre teoria da relatividade, é importante conhecer os conceitos formulados por Albert Einstein e sua importância para a Física Moderna.
Publicado por: Pâmella Raphaella MeloQuestões
-
Questão 1
(CFT-CE) Em 2005, Ano Mundial da Física, comemora-se o centenário da teoria da relatividade de Albert Einstein. Entre outras consequências, esta teoria poria fim à ideia do éter, meio material necessário, semelhantemente ao som, através do qual a luz se propagava. O jargão popular “tudo é relativo” certamente não se deve a ele, pois seus postulados estão fundamentados em algo absoluto: a velocidade da luz no vácuo – 300.000 km/s.
Hoje sabe-se que:
I. O som propaga-se no vácuo.
II. A luz propaga-se no vácuo.
III. A velocidade da luz no vácuo é a velocidade limite do universo.
É (são) verdadeira(s):
a) todas.
b) nenhuma.
c) somente II.
d) II e III.
e) somente III.
LETRA D
O som não se propaga no vácuo, já que é uma onda mecânica, necessitando de um meio para se deslocar, contudo a luz é uma onda eletromagnética, então pode se deslocar sem a necessidade de um meio. Além disso, a velocidade da luz no vácuo é a velocidade máxima atingida por qualquer partícula ou evento no universo.
-
Questão 2
(UFPE) Um astronauta é colocado a bordo de uma espaçonave e enviado para uma estação espacial a uma velocidade constante v = 0,8 c, onde c é a velocidade da luz no vácuo. No referencial da espaçonave, o tempo transcorrido entre o lançamento e a chegada na estação espacial foi de 12 meses. Qual o tempo transcorrido no referencial da Terra, em meses?
a) 5
b) 10
c) 20
d) 100
e) 200
LETRA C
Calcularemos o tempo transcorrido no referencial da Terra através da fórmula da dilatação do tempo:
\(∆t=γ\cdot∆t_o\)
O fator de Lorentz equivale a:
\(\gamma=\frac{1}{\sqrt{1-\frac{v^2}{c^2}}}\)
Então:
\(∆t=\frac{∆t_o}{\sqrt{1-\frac{v^2}{c^2}}}\)
em que ∆t é o tempo dilatado medido por quem está na plataforma na Terra e ∆to é o intervalo de tempo próprio medido por quem está na nave em movimento.
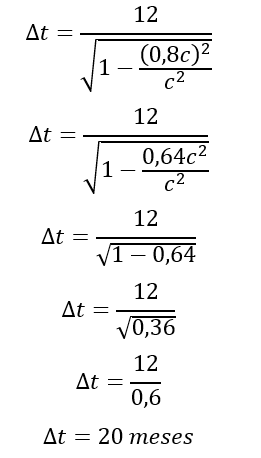
-
Questão 3
(UFMG) Observe esta figura:
Paulo Sérgio, viajando em sua nave, aproxima-se de uma plataforma espacial, com velocidade de 0,7 c, em que c é a velocidade da luz.
Para se comunicar com Paulo Sérgio, Priscila, que está na plataforma, envia um pulso luminoso em direção à nave. Com base nessas informações, é correto afirmar que a velocidade do pulso medida por Paulo Sérgio é de:
a) 0,7 c.
b) 1,0 c.
c) 0,3 c.
d) 1,7 c.
LETRA B
A velocidade do pulso medido por Paulo Sérgio é de 1,0 c, já que a velocidade da luz no vácuo é constante, não variando com a velocidade da nave.
-
Questão 4
(UFRGS) Assinale a alternativa que preenche corretamente as lacunas do texto a seguir, na ordem em que aparecem.
De acordo com a relatividade restrita, é ___________ atravessarmos o diâmetro da Via Láctea, uma distância de aproximadamente 100 anos-luz (equivalente a 1018 m), em um intervalo de tempo bem menor que 100 anos. Isso pode ser explicado pelo fenômeno de ___________ do comprimento, como visto pelo viajante, ou ainda pelo fenômeno de ___________ temporal, como observado por quem está em repouso em relação à galáxia.
a) impossível – contração – dilatação
b) possível – dilatação – contração
c) possível – contração – dilatação
d) impossível – dilatação – contração
e) impossível – contração – contração
LETRA C
De acordo com a relatividade restrita, é possível atravessarmos o diâmetro da Via Láctea, uma distância de aproximadamente 100 anos-luz (equivalente a 1018 m), em um intervalo de tempo bem menor que 100 anos. Isso pode ser explicado pelo fenômeno de contração do comprimento, como visto pelo viajante, ou ainda pelo fenômeno de dilatação temporal, como observado por quem está em repouso em relação à galáxia.
-
Questão 5
Um trem de 200 m se move a uma velocidade de 0,5 c quando percorre um túnel de 80 m, então qual o comprimento aproximado desse trem observado por alguém parado ao lado dos trilhos?
a) 129 m.
b) 142 m.
c) 156 m.
d) 168 m.
e) 173 m.
LETRA E
Calcularemos o comprimento desse trem através da fórmula da contração do comprimento:
\(L=\frac{L_o}{\gamma}\)
O fator de Lorentz equivale a:
\(\gamma=\frac{1}{\sqrt{1-\frac{v^2}{c^2}}}\)
Então:
\(L=\frac{L_o}{\frac{1}{\sqrt{1-\frac{v^2}{c^2}}}}\)
\(L=L_o\cdot\sqrt{1-\frac{v^2}{c^2}}\)
\(L=200\cdot\sqrt{1-\frac{\left(0,5c\right)^2}{c^2}}\)
\(L=200\cdot\sqrt{1-\frac{{0,25c}^2}{c^2}}\)
\(L=200\cdot\sqrt{1-0,25}\)
\(L=200\cdot\sqrt{0,75}\)
\(L\cong200\cdot0,866\)
\(L\cong173\ m\)
-
Questão 6
Analise qual das alternativas abaixo corresponde às teorias que englobam a teoria da relatividade:
I. Teoria da relatividade restrita.
II. Teoria da relatividade geral.
III. Teoria da relatividade conservada.
IV. Teoria da relatividade do tempo.
V. Está(ão) correta(s):
a) I e II.
b) III e IV.
c) I e III.
d) II e IV.
e) Todas estão incorretas.
LETRA A
A teoria da relatividade restrita e a teoria da relatividade geral são as teorias que fazem parte da teoria da relatividade.
-
Questão 7
De acordo com a teoria da relatividade, quais são as principais consequências da teoria da relatividade restrita?
I. Princípio da simultaneidade.
II. Curvatura do tecido espaço-tempo.
III. Contração do comprimento.
IV. Dilatação do tempo.
V. Comprovação da existência do éter.
Estão corretas as alternativas:
a) I, II e III.
b) I, III e IV.
c) II, III e IV.
LETRA B
As consequências da teoria da relatividade restrita são velocidade limite dos corpos, comprovação da inexistência do éter, princípio da simultaneidade, dilatação do tempo, contração do comprimento. Já a curvatura do tecido espaço-tempo está incluída na teoria da relatividade geral.
-
Questão 8
Existem dois postulados que fundamentam a teoria da relatividade, então analise quais das alternativas abaixo correspondem a esses postulados.
I. Princípio da relatividade restrita.
II. Princípio da relatividade geral.
III. Princípio de constância da velocidade da luz.
IV. Princípio de inconstância da velocidade da luz.
Está(ão) correta(s):
a) I e II.
b) III e IV.
c) I e III.
d) II e IV.
e) Todas estão incorretas.
LETRA C
Os postulados da teoria da relatividade desenvolvidos por Albert Einstein (1879-1955) em 1905 são o princípio da relatividade restrita e o princípio de constância da velocidade da luz.
-
Questão 9
Uma nave espacial se afasta de um planeta com velocidade de 0,3 c, em certo momento ela manda um sinal de rádio ao planeta. A partir dessas informações, determine a velocidade do sinal medido pelo observador na nave e a velocidade do sinal medido pelo observador no planeta.
a) 0,9 c.
b) 0,7 c.
c) 0,6 c.
d) 0,3 c.
e) A velocidade do sinal é c em ambos os casos.
LETRA E
A velocidade do sinal medido pelo observador na nave e pelo observador no planeta é c, já que ela não varia de acordo com o referencial adotado.
-
Questão 10
Ainda que a teoria da relatividade explique diversos fenômenos não observáveis a olho nu, ela é capaz de ser aplicada em diversas tecnologias utilizadas em nosso cotidiano, com exceção da(o):
a) GPS.
b) Reatores e bombas nucleares.
c) Eletroímas.
d) Sonares.
e) Tubos de raio catódico.
LETRA D
Os sonares não funcionam a partir da teoria da relatividade, mas através do princípio de reflexão das ondas sonoras.
-
Questão 11
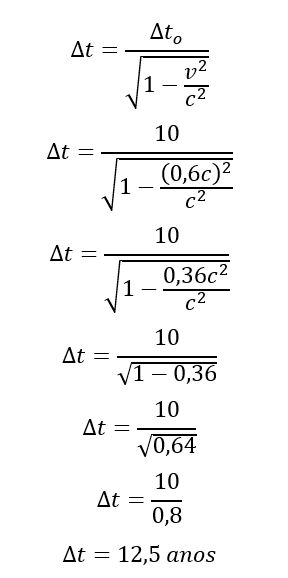
Um conjunto de astronautas viaja a bordo de uma nave espacial permanecendo em missão no decorrer de 10 anos, medidos no relógio da nave. Ao retornar à Terra, os astronautas percebem que já se passaram alguns anos, então, considerando que a velocidade medida da nave era de 0,6 c, calcule quantos anos se passaram na Terra.
a) 12,5 anos
b) 25 anos
c) 10 anos
d) 20 anos
e) 5 anos
LETRA A
Calcularemos o tempo que passou na Terra através da fórmula da dilatação do tempo:
\(∆t=γ\cdot∆t_o\)
O fator de Lorentz equivale a:
\(\gamma=\frac{1}{\sqrt{1-\frac{v^2}{c^2}}}\)
Então:
-
Questão 12
Analise as alternativas abaixo referentes às unidades de medida estudadas na teoria da relatividade:
I. A energia relativística é medida em calorias.
II. A massa da partícula é medida em metros.
III. A velocidade da luz é medida em metros por segundo.
IV. O comprimento é medido em metros.
V. O tempo é medido em segundos.
Está(ão) correta(s):
a) I, II e III.
b) I, IV, V.
c) II, III, IV.
d) I, II,V
e) III, IV, V
LETRA E
Abaixo vemos a correção em vermelho das alternativas incorretas.
I. Incorreta. A energia relativística é medida em Joule.
II. Incorreta. A massa da partícula é medida em quilograma.
III. Correta.
IV. Correta.
V. Correta.