Exercícios sobre Transformações Gasosas
(Uneb-BA) Em condições tais que um gás se comporta como ideal, as variáveis de estado assumem os valores 300 K, 2,0 m3 e 4,0 x 10 4 Pa, num estado A. Sofrendo certa transformação, o sistema chega ao estado B, em que os valores são 450 K, 3,0 m3 e p. O valor de p, em Pa, é:
(a) 1,3 x 10 4
(b) 2,7 x 10 4
(c) 4,0 x 10 4
(d) 6,0 x 10 4
(e) 1,2 x 10 5
No estado inicial (A), antes de sofrer a transformação, temos:
TA = 300 K
VA = 2,0 m3
PA = 4,0 x 10 4 Pa
O gás sofreu uma transformação e suas variáveis de estado no estado final (B) passaram a ser:
TB = 450 K
VA = 3,0 m3
Pb = ?
O exercício pede para calcularmos o valor da pressão, no estado final B, em pascal.
Para isso, basta aplicarmos a Lei Geral dos Gases Perfeitos e substituirmos os valores:
.jpg)
Letra (c)
Em um recipiente fechado, certa massa de gás ideal ocupa um volume de 12 litros a 293k. Se este gás for aquecido até 302k, sob pressão constante, seu volume será:
(a) 12,37 L
(b) 13,37 L
(c) 14,37 L
(d) 12 L
(e) 13 L
Dados:
No estado inicial (1), o gás tem:
V1 = 12 L
T1 = 293 k
Depois de aquecido, estado 2:
T1 = 302 k
V2 = ?
O enunciado da questão dá uma informação muito importante, ele fala que o gás foi aquecido sob pressão constante, logo, trata-se de uma transformação isobárica e, dessa forma, para resolvermos o problema, basta aplicarmos a lei de Gay – Lussac:
.jpg)
Letra (a)
(UFSC) O pneu de um automóvel foi regulado de forma a manter uma pressão interna de 21 libras-força por polegada quadrada, a uma temperatura de 14 ºC. Durante o movimento do automóvel, no entanto, a temperatura do pneu elevou-se a 55 ºC. Determine a pressão interna correspondente, em libras-força por polegada quadrada, desprezando a variação de volume do pneu.
Dados:
No estado inicial, que agora identificaremos por 1, as variáveis de estado eram:
p1 = 21 libras-força por polegada quadrada
T1 = 14 ºC
No estado final, estado 2:
T2 = 55 ºC
p2 = ?
O exercício pede para calcular a pressão em libras-força por polegada quadrada depois do aumento da temperatura, assim vamos calcular p2.
O enunciado do exercício pede para desprezarmos a variação de volume, assim fica evidente que se trata de um exercício envolvendo uma transformação isovolumétrica. Para resolvermos o exercício, basta aplicarmos a equação da transformação isovolumétrica, também conhecida como Lei de Charles. Antes de aplicarmos a Lei de Charles, devemos transformar a temperatura que está em ºC para kelvin (K), que é a escala de temperatura absoluta.
Transformando a temperatura de ºC para K:
Tk = Tc + 273
Assim:
(1): Tk = 14 + 273 = 287 k
(2): Tk = 55 + 273 = 328 k
Logo:
T1 = 287 K
T2 = 328 K
Aplicando a Lei de Charles:
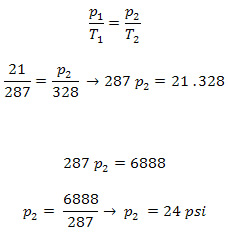
p2 = 24
.jpg "Exercício-Transformações Gasosas"){kind=spacer}
O gráfico acima mostra a isoterma de uma quantidade de gás que é levado de um estado 1 para um estado 2. O volume do estado 2, em litros, é:
(a) 2 L
(b) 4,5 L
(c) 6 L
(d) 4 L
(e) 3 L
No estado 1, temos:
P1 = 10 atm
V1 = 2,0 L
No estado 2:
P2 = 5 atm
V2 = ?
Como temos o gráfico de uma isoterma, indica que o gás foi do estado 1 para o dois sem que houvesse uma variação de temperatura, assim sendo, trata-se de uma transformação isotérmica. Para resolvermos a questão, vamos aplicar a lei da transformação isotérmica, também conhecida como Lei de Boyle – Mariotte:
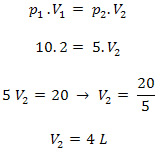
Letra (d)
