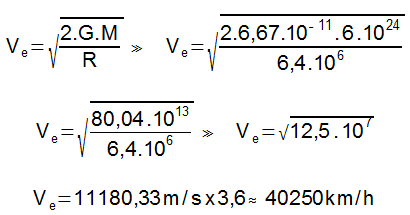Exercícios sobre velocidade de escape
Com estes exercícios, você pode avaliar o que sabe sobre a velocidade de escape, a mínima velocidade necessária para que um objeto possa sair de um planeta.
Publicado por: Joab Silas da Silva JúniorQuestões
-
Questão 1
(UEL-PR) Nem sempre é possível escapar da influência gravitacional de um planeta. No caso da Terra, a velocidade mínima de escape para um corpo de massa m é da ordem de 11,2 km/s. Em relação a essa velocidade, é correto afirmar que ela:
a) independe da massa do corpo, mas depende da massa da Terra.
b) independe da massa da Terra, mas depende da massa do corpo.
c) depende da massa da Terra e da massa do corpo.
d) independe da massa da Terra e da massa do corpo.
e) depende da massa do corpo e da massa do Sol.Letra A
A equação abaixo determina a velocidade de escape de um corpo para um planeta qualquer. Repare que não há na equação dependência da massa do objeto a ser lançado. A velocidade de escape depende da massa e do raio do planeta.
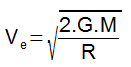
Os elementos dessa equação são:
Ve = Velocidade de escape;
G = Constante de gravitação universal. (G = 6,67 x 10 -11 N.m/kg2);
M = Massa do planeta;
R = Raio do planeta.
-
Questão 2
(ITA-SP) O raio do horizonte de eventos de um buraco negro corresponde à esfera dentro da qual nada, nem mesmo a luz, escapa da atração gravitacional por ele exercida. Por coincidência, esse raio pode ser calculado não relativisticamente como o raio para o qual a velocidade de escape é igual à velocidade da luz. Qual deve ser o raio do horizonte de eventos de um buraco negro com uma massa igual à massa da Terra?
Dados:
massa da Terra: 6,0.1024kg
velocidade da luz no vácuo: 3,0.108m/s
constante de gravitação universal: 6,67.10-11N.m2/kg2a) 9 µm.
b) 9 mm.
c) 30 cm.
d) 90 cm.
e) 3 km.Letra B
Aplicando a equação da velocidade de escape, devemos definir o valor de R, o raio da órbita de um objeto em movimento ao redor de um planeta. Para essas condições, o valor de R corresponderá justamente ao horizonte de eventos.
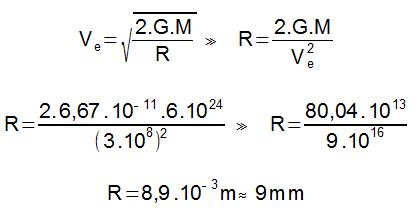
-
Questão 3
Marque alternativa correta a respeito da velocidade de escape.
a) A velocidade de escape é a máxima velocidade que um objeto precisa para conseguir abandonar um planeta.
b) A velocidade de escape de buracos negros é maior que a velocidade da luz.
c) Quanto maior a massa de um planeta maior será a velocidade de escape.
d) Quanto maior o raio do planeta, maior também será a velocidade escape.
e) Quanto maior a massa de um corpo, maior será sua velocidade de escape.
Letra B
Os buracos negros possuem velocidade com valor maior que a velocidade da luz, por isso, ao penetrar em um buraco negro, ela fica confinada. Os buracos negros apresentam velocidade de escape tão alta porque são extremamente massivos.
-
Questão 4
Determine a mínima velocidade, em km/h, necessária para que um objeto possa sair da superfície da Terra.
Dados: massa da Terra: 6,0.1024kg
Constante de gravitação universal: 6,67.10-11N.m2/kg2
Raio da Terra: 6,4 . 106 m.
a) 50.000
b) 40.500
c) 40.250
d) 25.000
e) 15.000
Letra C