30 exercícios de matemática básica
Teste seus conhecimentos por meio desta lista de exercícios que contém 30 exercícios de matemática básica.
Publicado por: Raul Rodrigues de OliveiraQuestões
-
Questão 1
(Enem 2020) Uma torneira está gotejando água em um balde com capacidade de 18 litros. No instante atual, o balde se encontra com ocupação de 50% de sua capacidade. A cada segundo caem 5 gotas de água da torneira, e uma gota é formada, em média, por 5×10-2 ml de água.
Quanto tempo, em hora, será necessário para encher completamente o balde, partindo do instante atual?
A) 2 × 101
B) 1 × 101
C) 2 × 10-2
D) 1 × 10-2
E) 1 × 10-3
Alternativa B.
Como a capacidade do balde é de 18 litros, e 50% dele está ocupado, sabemos que:50% de 18 = 0,5 × 18 = 9 litros, e que 9 litros correspondem a 9000 ml.
Sabemos que cada gota possui 5×10-2 ml = 0,05 ml cada. Como a cada segundo há 5 gotas, então é um total de 0,25 ml por segundo.
Logo será necessário um total de 9000 : 0,25 = 36000 segundos para preencher as 9000 ml restantes.
Sabemos que 3600 segundos correspondem a 10 horas, que em notação científica é igual a 1×101.
-
Questão 2
(Enem 2020) Um motociclista planeja realizar uma viagem cujo destino fica a 500 km de sua casa. Sua moto consome 5 litros de gasolina para cada 100 km rodados, e o tanque da moto tem capacidade para 22 litros. Pelo mapa, observou que no trajeto da viagem o último posto disponível para reabastecimento, chamado Estrela, fica a 80 km do seu destino. Ele pretende partir com o tanque da moto cheio e planeja fazer somente duas paradas para reabastecimento, uma na ida e outra na volta, ambas no posto Estrela. No reabastecimento para a viagem de ida, deve considerar também combustível suficiente para se deslocar por 200 km no seu destino.
A quantidade mínima de combustível, em litro, que esse motociclista deve reabastecer no posto Estrela na viagem de ida, que seja suficiente para fazer o segundo reabastecimento, é
A) 13.
B) 14.
C) 17.
D) 18.
E) 21.
Alternativa C.
Sabemos que 100 km consome 5 litros, logo serão consumidos
100 : 5 = 20 litros/km
Para fazer 420 km é necessário, então, um total de
420 : 20 = 21 litros
Sabemos que a capacidade do tanque é de 22 litros, então
22 – 21 = 1
Logo, sobrou 1 litro.
Agora o que nos interessa é o combustível necessário para que ele ande os 80 km restantes, mais 200 km dentro da cidade e os 80 km na volta, ou seja, um total de 360 km.
360 : 20 = 18 litros
Como restou 1 litro, então é necessário que ele abasteça no mínimo 18 – 1 = 17 L
-
Questão 3
(Enem 2020) Uma empresa de ônibus utiliza um sistema de vendas de passagens que fornece a imagem de todos os assentos do ônibus, diferenciando os assentos já vendidos, por uma cor mais escura, dos assentos ainda disponíveis. A empresa monitora, permanentemente, o número de assentos já vendidos e compara-o com o número total de assentos do ônibus para avaliar a necessidade de alocação de veículos extras.
Na imagem, tem-se a informação dos assentos já vendidos e dos ainda disponíveis em determinado instante.

A razão entre o número de assentos já vendidos e o total de assentos desse ônibus, no instante considerado na imagem, é
A) \(\frac{16}{42}\)
B) \(\frac{16}{26}\)
C) \(\frac{26}{42}\)
D) \(\frac{42}{26}\)
E) \(\frac{42}{16}\)
Alternativa A.
Sabemos que há um total de 16 assentos vendidos entre os 42 acentos, logo a razão entre o número de acentos vendidos em relação ao total de acentos do ônibus é de \(\frac{16}{42}\).
-
Questão 4
(IFG 2012) As medidas internas de um reservatório no formato de um paralelepípedo são de 2,5m de comprimento, 1,8m de largura e 1,2m de profundidade (altura). Se em determinado momento do dia esse reservatório está apenas com 70% de sua capacidade, a quantidade de litros que faltam para encher esse reservatório é igual a:
A) 1620
B) 1630
C) 1640
D) 1650
Alternativa A.
Primeiro calcularemos o volume:
V=2,5 ⋅1,8 ⋅1,2 =5,4 m3
Para transformar m3 para litros, basta multiplicar por 1000.
V= 7,65 ⋅1000 = 5400 l
Sabemos que 70% estão cheios, logo faltam 30% de 5400, o que é igual a:
0,3 ⋅5400 =1620
-
Questão 5
(Enem 2014) Os incas desenvolveram uma maneira de registrar quantidades e representar números utilizando um sistema de numeração decimal posicional: um conjunto de cordas com nós denominado quipus. O quipus era feito de uma corda matriz, ou principal (mais grossa que as demais), na qual eram penduradas outras cordas, mais finas, de diferentes tamanhos e cores (cordas pendentes). De acordo com a sua posição, os nós significavam unidades, dezenas, centenas e milhares Na Figura 1, o quipus representa o número decimal 2453. Para representar o “zero” em qualquer posição, não se coloca nenhum nó.
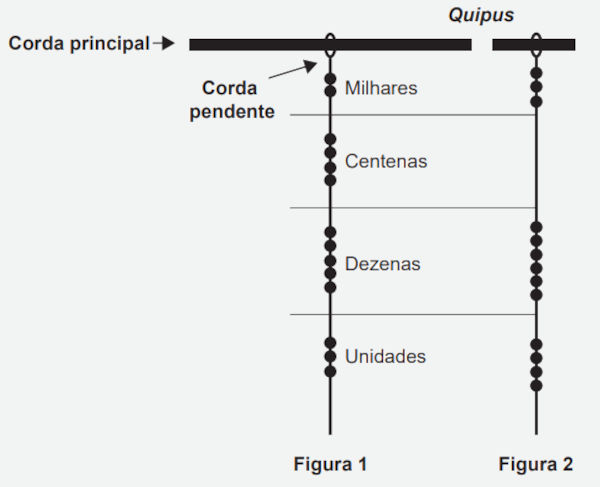
O número da representação do quipus da Figura 2, em base decimal, é
A) 364
B) 463
C) 3064
D) 3640
E) 4603
Alternativa C.
Há 3 unidades de milhar, 0 unidades nas centenas, 6 unidades de dezena e 4 unidades na unidade, sendo assim temos: 3064.
-
Questão 6
Durante a pandemia do coronavírus em 2020, foi declarado que o isolamento social é a melhor alternativa para retardar a propagação da doença. Sendo assim, a empresa de energia informou que não faria mais medições do consumo e que o valor da conta nesse período seria calculado pela média do valor pago pelas 6 últimas faturas. Gustavo é uma pessoa bastante precavida e, para não ter uma surpresa com a chegada das contas, resolveu antecipar-se calculando a média dos 6 meses anteriores para prever qual será o valor da próxima fatura. Sabendo que os valores das 6 últimas faturas são estes:
- janeiro - R$ 150
- fevereiro - R$ 120,50
- março - R$ 151,25
- abril - R$ 163,15
- maio - R$ 142,10
- junho - R$ 130
Qual será o valor pago por ele na próxima conta, aproximadamente?
A) R$ 143,00
B) R$ 144,00
C) R$ 145,00
D) R$ 146,00
E) R$ 150,00Alternativa A.
Calculando a média, temos que:
\(\overline{x} = \frac{150 + 120,50 + 151,25 + 163,15 + 142,10 + 130}{6} = 142,83\)
O valor pago por ele será de aproximadamente R$ 143,00
-
Questão 7
Uma empresa nacional de consórcio sofria com alto índice de inadimplência. Para avaliar o desempenho de cada uma das filiais, essa empresa desenvolveu o Índice de Aprovação do Cliente (IAC), que é a razão entre o número de clientes que pagaram todas as prestações durante um ano e o número de clientes que compraram cotas. Com a classificação do IAC, era possível avaliar o desempenho da empresa, de acordo com o seguinte critério:
- Ótimo → maior ou igual a 0,8.
- Bom → maior ou igual a 0,6 e menor que 0,8.
- Regular → maior ou igual a 0,5 e menor que 0,6.
- Ruim → maior ou igual a 0,3 e menor que 0,5.
- Péssimo → menor que 0,3.
Sabendo que a filial da cidade de Mozarlândia vendeu 960 cotas de consórcio e que dessas cotas um total de 346 clientes não pagaram, o desempenho dessa filial foi classificado como:
A) ótimo.
B) bom.
C) regular.
D) ruim.
E) péssimo.
Alternativa B
Se 346 clientes não pagaram, então 960 – 346 = 614. Fazendo a divisão, temos que:
614 : 960 = 0,63
Logo, o resultado foi bom, pois é maior que 0,6 e menor que 0,8.
-
Questão 8
(Enem 2007) Estima-se que haja, no Acre, 209 espécies de mamíferos, distribuídas conforme a tabela a seguir:
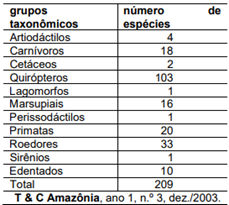
Deseja-se realizar um estudo comparativo entre três dessas espécies de mamíferos: uma do grupo cetáceos, outra do grupo primatas e a terceira do grupo roedores. O número de conjuntos distintos que podem ser formados com essas espécies para esse estudo é igual a:
A) 1320
B) 2090
C) 5845
D) 6600
E) 7245
Alternativa A.
Sabemos que há 2 cetáceos, 20 primatas e 33 roedores. Então, pelo princípio fundamental da contagem, o número de conjuntos distintos possíveis será:
2 · 20 · 33 = 1320
-
Questão 9
(Enem 2012) O diretor de uma escola convidou os 280 alunos de terceiro ano a participarem de uma brincadeira. Suponha que existem 5 objetos e 6 personagens numa casa de 9 cômodos; um dos personagens esconde um dos objetos em um dos cômodos da casa. O objetivo da brincadeira é adivinhar qual objeto foi escondido por qual personagem e em qual cômodo da casa o objeto foi escondido.
Todos os alunos decidiram participar. A cada vez um aluno é sorteado e dá a sua resposta. As respostas devem ser sempre distintas das anteriores, e um mesmo aluno não pode ser sorteado mais de uma vez. Se a resposta do aluno estiver correta, ele é declarado vencedor e a brincadeira é encerrada. O diretor sabe que algum aluno acertará a resposta porque há:
A) 10 alunos a mais do que possíveis respostas distintas.
B) 20 alunos a mais do que possíveis respostas distintas.
C) 119 alunos a mais do que possíveis respostas distintas.
D) 260 alunos a mais do que possíveis respostas distintas.
E) 270 alunos a mais do que possíveis respostas distintas.
Alternativa A.
Pelo princípio fundamental da contagem, o número de possíveis respostas será igual ao produto das quantidades de personagens, objetos e cômodos.
5 · 6 · 9 = 270
Como o número de alunos é 280, então a diferença entre a quantidade de número de alunos e a quantidade de possibilidades é 10.
-
Questão 10
(Enem 2017) Para a Olimpíada de 2012, a piscina principal do Centro Aquático de Londres, medindo 50 metros de comprimento, foi remodelada para ajudar os atletas a melhorar suas marcas. Observe duas das melhorias:
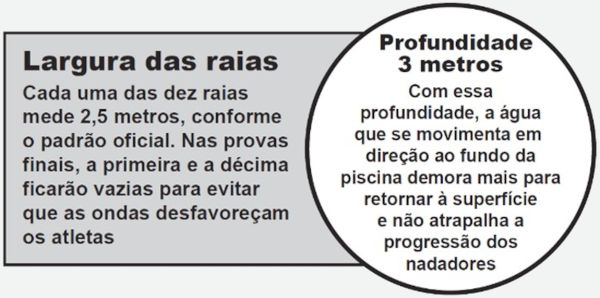
A capacidade da piscina em destaque, em metro cúbico, é igual a:
A) 3750.
B) 1500.
C) 1250.
D) 375.
E) 150.Alternativa A.
Sabemos que há 10 raias de 2,5 metros, logo temos
10 ⋅ 2,5 = 25 metros de largura
O comprimento é 50 metros e a profundidade, 3 metros, então temos que:
25 ⋅ 50 ⋅ 3 = 3750m3
-
Questão 11
(Enem 2017) Em uma embalagem de farinha, encontra-se a receita de um bolo, sendo parte dela reproduzida a seguir:

Possuindo apenas a colher medida indicada na receita, uma dona de casa teve que fazer algumas conversões para poder medir com precisão a farinha. Considere que a farinha e o fermento possuem densidades iguais.
Cada xícara indicada na receita é equivalente a quantas colheres medidas?
A) 10
B) 20
C) 40
D) 80
E) 320
Alternativa B.
Para calcular a quantidade de gramas em uma xícara, basta dividir
640 : 4 = 160 g
Para calcular a capacidade de uma colher de medida, basta dividir
16 : 2 = 8 g
Então, uma xícara vai valer
160 g : 8 g = 20 colheres
-
Questão 12
(Enem 2019) O rótulo da embalagem de um cosmético informa que a dissolução de seu conteúdo, de acordo com suas especificações, rende 2,7 litros desse produto pronto para o uso. Uma pessoa será submetida a um tratamento estético em que deverá tomar um banho de imersão com esse produto numa banheira com capacidade de 0,3 m3. Para evitar o transbordamento, essa banheira será preenchida em 80% de sua capacidade.
Para esse banho, o número mínimo de embalagens desse cosmético é:
A) 9.
B) 12.
C) 89.
D) 112.
E)134.
Alternativa C.
Se a capacidade da banheira é de 0,3 m3, sabemos que 0,3 m3 correspondem a 300 L.
80% de 300 = 0,8 · 300 = 240 L
Como cada embalagem rende 2,7 litros, então temos que:
240 : 2,7 = 88,88…
Sendo assim, serão necessárias 89 embalagens.
-
Questão 13
(Enem 2012) Uma mãe recorreu à bula para verificar a dosagem de um remédio que precisava dar a seu filho. Na bula, recomendava-se a seguinte dosagem: 5 gotas para cada 2 kg de massa corporal a cada 8 horas.
Se a mãe ministrou corretamente 30 gotas do remédio a seu filho a cada 8 horas, então a massa corporal dele é de:
A) 12 kg.
B) 16 kg.
C) 24 kg.
D) 36 kg.
E) 75 kg.
Alternativa A.
As grandezas são a quantidade de gotas e a massa da criança. Sabemos que quanto maior a massa, maior o número de gotas a serem ministradas para a criança. Então temos grandezas diretamente proporcionais. Logo:
\(\frac{5}{30} = \frac{2}{x}\)
Multiplicando cruzado:
\(5x = 30 ⋅ 2\)
\(5x = 60\)
\(x = \frac {60}{5}\)
\(x=12\)
-
Questão 14
(Enem 2016) Um posto de saúde registrou a quantidade de vacinas aplicadas contra febre amarela nos últimos cinco meses:
- 1º mês: 21.
- 2º mês: 22.
- 3º mês: 25.
- 4º mês: 31.
- 5º mês: 21.
No início do primeiro mês, esse posto de saúde tinha 228 vacinas contra febre amarela em estoque. A política de reposição do estoque prevê a aquisição de novas vacinas no início do sexto mês, de tal forma que a quantidade inicial em estoque para os próximos meses seja igual a 12 vezes a média das quantidades mensais dessas vacinas aplicadas nos últimos cinco meses.
Para atender essas condições, a quantidade de vacinas contra febre amarela que o posto de saúde deve adquirir no início do sexto mês é
A) 156.
B) 180.
C) 192.
D) 264.
E) 288.
Alternativa B.
O total de vacinas aplicadas foi igual a:
21 + 22 + 25 + 31 + 21 = 120
Restou um total de
228 – 120 = 108 vacinas
A média de vacinas mensal é igual a
120 : 5 = 24 vacinas/mês
Como queremos 12 vezes a média dos 5 primeiros meses, será o total de
12 · 24 = 288 vacinas
Então, é necessário adquirir um total de
288 – 108 = 180 vacinas
-
Questão 15
(Enem 2016) A permanência de um gerente em uma empresa está condicionada à sua produção no semestre. Essa produção é avaliada pela média do lucro mensal do semestre. Se a média for, no mínimo, de 30 mil reais, o gerente permanece no cargo; caso contrário, ele será despedido. O quadro mostra o lucro mensal, em milhares de reais, dessa empresa, de janeiro a maio do ano em curso.

Qual deve ser o lucro mínimo da empresa no mês de junho, em milhares de reais, para o gerente continuar no cargo no próximo semestre?
A) 26
B) 29
C) 30
D) 31
E) 35
Alternativa E.
A média entre os 6 meses tem que ser pelo menos igual a 30. Sendo x o faturamento do mês de junho, temos que:
(21 + 35 + 21 + 30 + 38 + x) : 6 = 30
(145 + x) : 6 = 30
145 + x = 30 · 6
145 + x = 180
x = 180 – 145
x = 35
-
Questão 16
(IFG 2019) Os babilônicos talvez tenham usado a fórmula abaixo para obter aproximações interessantes de raízes quadradas de números não quadrados perfeitos.
\(\sqrt{a^2 + b} \approx a + \frac{b}{2a}\)
Atribuindo a = 4/3 e b = 2/9 nessa fórmula, é correto afirmar que obtemos a aproximação:
A) \(\sqrt{2} \approx \frac{17}{12}\)
B) \(\sqrt{2} \approx \frac{15}{12}\)
C) \(\sqrt{\frac{15}{12}} \approx 2\)
D) \(\sqrt{2} \approx 1.426 ...\)
Alternativa A.
Vamos substituir os valores de a e b na equação:
\(\sqrt{(\frac{4}{3})^2 + \frac{2}{9}} \approx \frac{4}{3} + \frac{\frac{2}{9}}{2 \cdot \frac{4}{3}}\)
\(\sqrt{\frac{16}{9} + \frac{2}{9}} \approx \frac{4}{3} + \frac{\frac{2}{9}}{\frac{8}{3}}\)
\(\sqrt{\frac{18}{9}} \approx \frac{4}{3} +\frac{2}{9} \cdot \frac{3}{8}\)
\(\sqrt{2} \approx \frac{4}{3} +\frac{6}{72}\)
\(\sqrt{2} \approx \frac{4}{3} +\frac{1}{12}\)
\(\sqrt{2} \approx \frac{16\ +\ 1}{12}\)
\(\sqrt{2} \approx \frac{17}{12}\)
-
Questão 17
(Enem 2010)
No monte de Cerro Armazones, no deserto de Atacama, no Chile, ficará o maior telescópio da superfície terrestre, o Telescópio Europeu Extremamente Grande (E-ELT). O E-ELT terá um espelho primário de 42 m de diâmetros, “maior olho do mundo voltado para o céu”.
Disponível em: http://www.estadao.com.br. Acesso em: 27 abr. 2010 (adaptado).
Ao ler esse texto em uma sala de aula, uma professora fez uma suposição de que o diâmetro do olho humano mede aproximadamente 2,1 cm.
Qual a razão entre o diâmetro aproximado do olho humano, suposto pela professora, e o diâmetro do espelho primário do telescópio citado?
A) 1 : 20
B) 1 : 100
C) 1 : 200
D) 1 : 1000
E) 1 : 2000
Alternativa E.
Sabemos que 42 metros equivalem a 4200 cm, então:
2,1 : 4200
Dividindo por 2,1 dos dois lados, temos que a escala será de:
1 : 2000
-
Questão 18
(Enem 2011)
Cerca de 20 milhões de brasileiros vivem na região coberta pela Caatinga, em quase 800 mil km2 de área. Quando não chove, o homem do sertão e sua família precisam caminhar quilômetros em busca da água dos açudes. A irregularidade climática é um dos fatores que mais interferem na vida do sertanejo.
Disponível em: http://www.wwf.org.br. Acesso em: 23 abr. 2010.
Segundo esse levantamento, a densidade demográfica da região coberta pela Caatinga, em habitantes por km², é de:
A) 250.
B) 25.
C) 2,5.
D) 0,25.
E) 0,025.
Alternativa B.
Para encontrar a densidade demográfica, vamos dividir 20.000.000 por 800.000:
20.000.000 : 800.000 = 25
-
Questão 19
(Enem PPL 2011) Na zona rural, a utilização de unidades de medida como o hectare é bastante comum. O hectare equivale à área de um quadrado de lado igual a 100 metros. Na figura, há a representação de um terreno por meio da área em destaque. Nesta figura, cada quadrado que compõe esta malha representa uma área de 1 hectare.

O terreno em destaque foi comercializado pelo valor R$ 3.600.000. O valor do metro quadrado desse terreno foi de
A) R$ 30.
B) R$ 300.
C) R$ 360.
D) R$ 3600.
E) R$ 300.000.
Alternativa A.
Primeiro calcularemos a área do quadrado:
A = l2
A = 1002 = 10.000
Há 12 quadrados na área, então 12 ⸳ 10.000 = 120.000 m2. Para saber o custo de cada quadrado, basta dividir o valor pago pelo terreno pela sua área:
3.600.000 : 120.000 = R$ 30
-
Questão 20
(Enem 2023)
O calendário maia apresenta duas contagens simultâneas de anos, o chamado ano Tzolkim, composto por 260 dias e que determinava o calendário religioso, e o ano Haab, composto por 365 dias e que determinava o calendário agrícola. Um historiador encontrou evidências de que gerações de uma mesma família governaram certa comunidade maia pelo período de 20 ciclos, sendo cada ciclo formado por 52 anos Haab.
Disponível em: www.suapesquisa.com. Acesso em: 20 ago. 2014.
De acordo com as informações fornecidas, durante quantos anos Tzolkim aquela comunidade maia foi governada por tal família?
A) 741
B) 1040
C) 1460
D) 2100
E) 5200
Alternativa C.
Sabemos que 1 ano Tzolkim corresponde a 260 dias.
Para saber a quantidade de anos Tzolkim que a família governou precisamos saber o total de dias de 20 ciclos Haab:
1 ano Haab = 365 dias
1 ciclo em anos Haab = 18980 dias
20 ciclos Haab = 379600 dias
Para converter 20 ciclos Haab em anos Tzolkim, devemos dividir 379600 por 260.
379600 : 260=1460
Então, a comunidade foi governada pela família durante 1460 anos Tzolkim.
-
Questão 21
(Enem 2022) Ao escutar a notícia de que um filme recém-lançado arrecadou, no primeiro mês de lançamento, R$ 1,35 bilhão em bilheteria, um estudante escreveu corretamente o número que representa essa quantia, com todos os seus algarismos.
O número escrito pelo estudante foi
A) 135 000,00.
B) 1 350 000,00.
C) 13 500 000,00.
D) 135 000 000,00.
E) 1 350 000 000,00
Alternativa E.
1,350 bilhão é igual a 1 bilhão e 350 milhões, que pode ser representado por:
1 350 000 000,00
-
Questão 22
(Enem 2013)
O contribuinte que vende mais de R$ 20 mil de ações em Bolsa de Valores em um mês deverá pagar Imposto de Renda. O pagamento para a Receita Federal consistirá em 15% do lucro obtido com a venda das ações.
Disponível em: www1.folha.uol.com.br. Acesso em: 26 abr. 2010 (adaptado).
Um contribuinte que vende por R$ 34 mil um lote de ações que custou R$ 26 mil terá de pagar de Imposto de Renda à Receita Federal o valor de:
A) R$ 900,00.
B) R$ 1200,00.
C) R$ 2100,00.
D) R$ 3900,00.
E) R$ 5100,00.
Alternativa B.
Calculando o lucro, temos que:
L = 34000 - 26000 = 8000
Sabendo que o Imposto de Renda que esse contribuinte terá que pagar será 15% do lucro, então temos que:
0,15 ⋅ 8 000 = 1 200
-
Questão 23
(Enem 2022) Uma instituição de ensino superior ofereceu vagas em um processo seletivo de acesso a seus cursos. Finalizadas as inscrições, foi divulgada a relação do número de candidatos por vaga em cada um dos cursos oferecidos. Esses dados são apresentados no quadro.
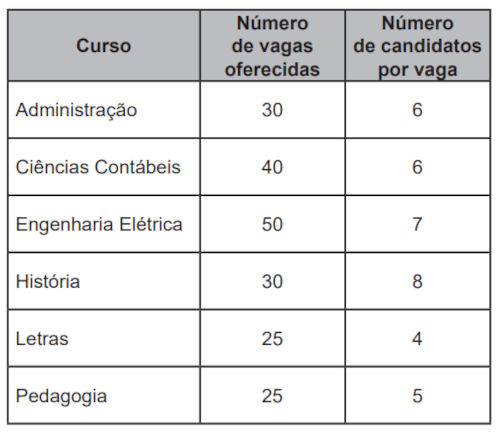
Qual foi o número total de candidatos inscritos nesse processo seletivo?
A) 200
B) 400
C) 1200
D) 1235
E) 7200
Alternativa D.
Para calcular o número total de candidatos, temos que:
30 ⋅ 6 + 40 ⋅ 6 + 50 ⋅ 7 + 30 ⋅ 8 + 25 ⋅ 4 + 25 ⋅ 5
180 + 240 + 350 + 240 + 100 + 125
1235
-
Questão 24
(Enem 2020) Um hotel de 3 andares está sendo construído. Cada andar terá 100 quartos. Os quartos serão numerados de 100 a 399 e cada um terá seu número afixado à porta. Cada número será composto por peças individuais, cada uma simbolizando um único algarismo.
Qual a quantidade mínima de peças, simbolizando o algarismo 2, necessárias para identificar o número de todos os quartos?
A) 160
B) 157
C) 130
D) 120
E) 60
Alternativa A.
Primeiro vamos listar esses números:
De 100 até 199:
102, 112, 120, 121, 122, 123, 124, 125, 126, 127, 128, 129, 132, 142, 152, 162, 172, 182, 192
Logo, o algarismo 2 aparece 20 vezes.De 300 até 399, o raciocínio é análogo, pois 2 aparece 20 vezes:
302, 312, 320, 321, 322, 323, 324, 325, 326, 327, 328, 329, 332, 342, 352, 362, 372, 382, 392
De 200 a 299, sabemos que todos os 100 números começam com 2. Além disso, usando o raciocínio anterior, o 2 aparece na unidade ou na dezena um total de 20 vezes, logo 120 vezes.
20 + 120 + 20 = 160
-
Questão 25
(Enem 2020) Pesquisadores da Universidade de Tecnologia de Viena, na Áustria, produziram miniaturas de objetos em impressoras 3D de alta precisão. Ao serem ativadas, tais impressoras lançam feixes de laser sobre um tipo de resina, esculpindo o objeto desejado. O produto final da impressão é uma escultura microscópica de três dimensões, como visto na imagem ampliada.

A escultura apresentada é uma miniatura de um carro de Fórmula 1, com 100 micrômetros de comprimento. Um micrômetro é a milionésima parte de um metro.
Usando notação científica, qual é a representação do comprimento dessa miniatura, em metro?
A) 1,0 x 10-1
B) 1,0 x 10-3
C) 1,0 x 10-4
D) 1,0 x 10-6
E) 1,0 x 10-7
Alternativa C.
Sabemos que 1 micrometro possui:
1 ⋅ 10-6
Como a miniatura possui 100 micrometros, então temos que:
1 ⋅ 10-6 ⋅ 100 = 1 ⋅ 10-4
-
Questão 26
(Enem 2023) Um tipo de semente necessita de bastante água nos dois primeiros meses após o plantio. Um produtor pretende estabelecer o melhor momento para o plantio desse tipo de semente, nos meses de outubro a março. Após consultar a previsão do índice mensal de precipitação de chuva (ImPC) da região onde ocorrerá o plantio, para o período chuvoso de 2020-2021, ele obteve os seguintes dados:
- outubro/2020: ImPC = 250 mm.
- novembro/2020: ImPC = 150 mm.
- dezembro/2020: ImPC = 200 mm.
- janeiro/2021: ImPC = 450 mm.
- fevereiro/2021: ImPC = 100 mm.
- março/2021: ImPC = 200 mm.
Com base nessas previsões, ele precisa escolher dois meses consecutivos em que a média mensal de precipitação seja a maior possível.
No início de qual desses meses o produtor deverá plantar esse tipo de semente?
A) Outubro.
B) Novembro.
C) Dezembro.
D) Janeiro.
E) Fevereiro.
Alternativa D.
Outubro + novembro
250 + 150 = 400 mmNovembro + dezembro
150 + 200 = 350mmDezembro + janeiro
200 + 450 = 650mmJaneiro + fevereiro
450 + 100 = 550 mmFevereiro + março
100 + 200 = 300 mmO maior valor se inicia em dezembro e termina em janeiro.
-
Questão 27
(Enem 2015) Alguns exames médicos requerem uma ingestão de água maior do que a habitual. Por recomendação médica, antes do horário do exame, uma paciente deveria ingerir 1 copo de água de 150 mililitros a cada meia hora, durante as 10 horas que antecederiam um exame. A paciente foi a um supermercado comprar água e verificou que havia garrafas dos seguintes tipos:
- Garrafa I: 0,15 litro.
- Garrafa II: 0,30 litro.
- Garrafa III: 0,75 litro.
- Garrafa IV: 1,50 litro.
- Garrafa V: 3,00 litros.
A paciente decidiu comprar duas garrafas do mesmo tipo, procurando atender à recomendação médica e, ainda, de modo a consumir todo o líquido das duas garrafas antes do exame.
Qual o tipo de garrafa escolhida pela paciente?
A) I
B) II
C) III
D) IV
E) V
Alternativa D.
Como a paciente deve tomar um copo a cada meia hora, ela tomará 2 copos por hora e 20 copos em 10 horas.
20 ⋅ 150 = 3000 ml = 3 litros
Então a garrafa IV a atende de forma que ela possua as 2 garrafas.
-
Questão 28
Quantas peças de cerâmica de 5 cm por 10 cm serão utilizadas para cobrir uma sala de 4 m de largura por 5 m de comprimento?
A) 40
B) 400
C) 4000
D) 40000
E) 400000
Alternativa C.
Primeiro, sabemos que a área da cerâmica é igual a
5 ⋅ 10 = 50 cm
Transformando o comprimento da sala para centímetros e calculando sua área, temos que:
400 ⋅ 500 = 200000 cm2
Agora basta dividir
200000 : 50 = 4000
-
Questão 29
(Enem 2023) Um pescador tem um custo fixo diário de R$ 900,00 com combustível, iscas, manutenção de seu barco e outras pequenas despesas. Ele vende cada quilograma de peixe por R$ 5,00. Sua meta é obter um lucro mínimo de R$ 800,00 por dia. Sozinho, ele consegue, ao final de um dia de trabalho, pescar 180 kg de peixe, o que é suficiente apenas para cobrir o custo fixo diário. Portanto, precisa contratar ajudantes, pagando para cada um R$ 250,00 por dia de trabalho. Além desse valor, 4% da receita obtida pela venda de peixe é repartida igualmente entre os ajudantes. Considerando o tamanho de seu barco, ele pode contratar até 5 ajudantes. Ele sabe que com um ajudante a pesca diária é de 300 kg e que, a partir do segundo ajudante contratado, aumenta-se em 100 kg a quantidade de peixe pescada por ajudante em um dia de trabalho.
A quantidade mínima de ajudantes que esse pescador precisa contratar para conseguir o lucro diário pretendido é
A) 1
B) 2
C) 3
D) 4
E) 5
Alternativa D.
O pescador deseja obter um lucro de pelo menos R$ 800,00.
Sabemos que cada quilo de peixe é vendido por R$ 5,00, os custos diários são de R$ 900,00, e ele pagará R$ 250,00 a cada ajudante. Além disso, ele separará 4% da receita para dividir entre os ajudantes.
Vamos calcular quantos ajudantes são necessários para atingir o lucro desejado:
- Com 1 ajudante:
Quantidade total de peixe pescado: 300 kg (dado no enunciado).
Receita: 5 x 300 = R$ 1500,00.
Subtraindo o custo do ajudante, a porcentagem e o custo diário, temos:
1500 – 250 – 0,04 x 1500 – 900 = R$ 290,00 (não alcançou o lucro esperado).
- Com 2 ajudantes:
Quantidade total de peixe pescado: 400 kg (300 kg do primeiro ajudante + 100 kg do segundo).
Receita: 5 x 400 = R$ 2000,00.
Subtraindo o pagamento dos dois ajudantes, a porcentagem e o custo diário, temos:
2000 – 2 x 250 – 0,04 x 2000 – 900 = R$ 520,00 (não alcançou o lucro esperado).
- Com 3 ajudantes:
Quantidade total de peixe pescado: 500 kg (300 kg com o primeiro ajudante + 100 kg com o segundo + 100 kg com o terceiro).
Receita: 5 x 500 = R$ 2500,00.
Subtraindo o pagamento dos ajudantes, a porcentagem e o custo diário, temos:
2500 – 3 x 250 – 0,04 x 2500 – 900 = R$ 550,00 (não alcançou o lucro esperado).
- Com 4 ajudantes:
Quantidade total de peixe pescado: 600 kg (300 kg com o primeiro ajudante + 100 kg com o segundo + 100 kg com o terceiro + 100 kg com o quarto).
Receita: 5 x 600 = R$ 3000,00.
Subtraindo o pagamento dos ajudantes, a porcentagem e o custo diário, temos:
3000 – 4 x 250 – 0,04 x 3000 – 900 = R$ 980,00 (atingiu o lucro esperado).
Portanto, o pescador precisará contratar 4 ajudantes para alcançar o lucro diário desejado.
-
Questão 30
(Enem 2023) Os 100 funcionários de uma empresa estão distribuídos em dois setores: produção e administração.
Os funcionários de um mesmo setor recebem salários com valores iguais. O quadro apresenta a quantidade de funcionários por setor e seus respectivos salários.
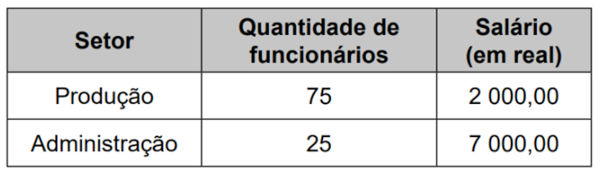
A média dos salários dos 100 funcionários dessa empresa, em real, é
A) 2000,00.
B) 2500,00.
C) 3250,00.
D) 4500,00.
E) 9000,00.
Alternativa C.
Para calcular a média salarial, temos que
\(\frac{75\ \cdot \ 2000 \ +\ 25\ \cdot\ 7000}{100} = \frac{150000\ + \ 175000}{100} = \frac{325000}{100} = 3250,00\)