30 exercícios sobre raciocínio lógico
Analise a sequência a seguir:
1, 6, 12, 19, 27, ...
Podemos afirmar que o próximo número dessa sequência é:
A) 35
B) 36
C) 37
D) 38
E) 39
Alternativa B
Analisando a sequência, temos que, dado o primeiro termo, para encontrar o segundo, somou-se 5 a ele:
1 + 5 = 6
Para o próximo termo, somou-se 6 ao segundo termo:
6 + 6 = 12
Para o próximo, somou-se 7 ao terceiro termo:
12 + 7 = 19
E assim sucessivamente:
19 + 8 = 27
Sendo assim, o próximo termo será 27 + 9 = 36.
Maria decidiu contratar uma empresa para realizar o transporte de seus móveis para sua nova casa em outra cidade. Após pesquisar, encontrou duas empresas com as seguintes tarifas:
Empresa X: Cobra uma taxa fixa de R$ 150 mais R$ 2 por quilômetro rodado.
Empresa Y: Cobra apenas R$ 2,75 por quilômetro rodado, sem taxa fixa.
Sabendo que a distância entre as duas cidades é de 180 quilômetros e que Maria tem um orçamento de R$ 500 para o transporte, qual das alternativas abaixo é verdadeira?
A) Maria deve contratar a Empresa X, pois ela tem o menor custo.
B) Maria deve contratar a Empresa Y, pois ela tem o menor custo.
C) Maria pode contratar qualquer uma das duas empresas, pois elas têm o mesmo custo.
D) Maria não pode contratar nenhuma das duas empresas, pois o custo de ambas é maior que o seu orçamento.
Alternativa B
Sabemos que a distância entre as cidades é de 180 km e que o orçamento de Maria é de R$ 500.
→ Empresa X
- Tarifa fixa: R$ 150
- Custo por km: R$ 2
Cálculo do custo da Empresa X:
Custo X = 150+2 ⋅180
Custo X = 150+360
Custo X = 510
O custo total com a Empresa X é R$ 510.
→ Empresa Y
- Custo por km: R$ 2,75 (sem tarifa fixa)
Cálculo do custo da Empresa Y:
Custo Y = 2,75 ⋅180
Custo Y = 495
O custo total com a Empresa Y é R$ 495.
A alternativa correta é a B: Maria deve contratar a Empresa Y, pois ela tem o menor custo.
Considere a sequência de números: 5, 11, 18, 26, 35, ...
Qual será o próximo número dessa sequência?
A) 43
B) 44
C) 45
D) 46
E) 47
Alternativa C
Sequência: 5, 11, 18, 26, 35, ...
Vamos observar as diferenças entre os termos consecutivos:
- 11 – 5 = 6
- 18 – 11 = 7
- 26 – 18 = 8
- 35 – 26 = 9
A sequência tem uma diferença que aumenta em 1 a cada termo (+6, +7, +8, +9, ...).
Para encontrar o próximo número, somamos 10 ao último termo:
35 + 10 = 45
Observe a seguinte sequência: 7, 14, 21, 28, 35, 42 ...
Qual é o próximo número que completa a sequência?
A) 48
B) 49
C) 50
D) 51
E) 52
Alternativa B
Note que:
14 – 7 = 7
21 – 14 = 7
28 – 21 = 7
35 – 28 = 7
42 – 35 = 7
Sendo assim, a sequência aumenta de 7 em 7, logo, sabemos que 42 + 7 = 49.
(Enem 2023) Um tipo de semente necessita de bastante água nos dois primeiros meses após o plantio. Um produtor pretende estabelecer o melhor momento para o plantio desse tipo de semente nos meses de outubro a março. Após consultar a previsão do índice mensal de precipitação de chuva (ImPC) da região onde ocorrerá o plantio, para o período chuvoso de 2020-2021, ele obteve os seguintes dados:
• outubro/2020: ImPC = 250 mm;
• novembro/2020: ImPC = 150 mm;
• dezembro/2020: ImPC = 200 mm;
• janeiro/2021: ImPC = 450 mm;
• fevereiro/2021: ImPC = 100 mm;
• março/2021: ImPC = 200 mm.
Com base nessas previsões, ele precisa escolher dois meses consecutivos em que a média mensal de precipitação seja a maior possível.
No início de qual desses meses o produtor deverá plantar esse tipo de semente?
A) Outubro.
B) Novembro.
C) Dezembro.
D) Janeiro.
E) Fevereiro.
Alternativa C
Calculando as somas dos meses de 2 em 2:
- Outubro + novembro = 250 + 150 = 400 mm.
- Novembro + dezembro = 150 + 200 = 350 mm.
- Dezembro + janeiro = 200 + 450 = 650 mm.
- Janeiro + fevereiro = 450 + 100 = 550 mm.
- Fevereiro + março = 100 + 200 = 300 mm.
Então, o maior valor é de 650 mm, começando em dezembro e terminando em janeiro.
O dia em que Marcos fez 50 anos, seu primeiro neto nasceu. Há 10 anos, a idade de Marcos era 6 vezes a idade de seu neto.
Hoje, a idade do neto é um número:
A) múltiplo de 3.
B) múltiplo de 4.
C) primo.
D) divisor de 42.
E) divisor de 48.
Alternativa B
Quando Marcos tinha 50 anos, seu neto nasceu. Isso significa que a diferença de idade entre eles é de 50 anos:
x = y + 50
Há 10 anos, a idade de Marcos era 6 vezes a idade de seu neto:
x – 10 = 6 (y − 10)
Substituindo x = y + 50, temos que:
y + 50 – 10 = 6y – 60
y + 40 = 6y – 60
y – 6y = -60 – 40
-5y = -100
y = (-100) : (-5)
y = 20
Das alternativas, sabemos 20 é múltiplo de 4.
Ana, Beatriz e Cárita têm diferentes idades. Sabemos que:
- A soma das idades de Ana e Beatriz é 36 anos.
- A soma das idades de Beatriz e Cárita é 44 anos.
- A soma das idades de Ana e Cárita é 38 anos.
Qual é a idade de Cárita?
A) 16
B) 23
C) 26
D) 28
E) 30
Alternativa B
Sabemos que:
A + B = 36
B + C = 44
A + C = 38
Então, temos que:
A = 36 – B
Substituindo A na terceira equação:
36 – B + C = 38
-B + C = 38 – 36
-B + C = 2
Sabemos então que:
B + C = 44
-B + C = 2
Logo, temos que:
B – B + C + C = 44 + 2
2C = 46
C = 46 : 2
C = 23
Desse modo, Cárita tem 23 anos.
Em uma fazenda, há galinhas e vacas. Sabendo que há um total de 32 cabeças e 86 pés, quantas galinhas e quantas vacas há na fazenda?
A) 13 galinhas e 19 vacas
B) 14 galinhas e 18 vacas
C) 15 galinhas e 15 vacas
D) 16 galinhas e 14 vacas
E) 21 galinhas e 11 vacas
Alternativa E
Dados
- g é o número de galinhas (cada uma tem 1 cabeça e 2 pés).
- v é o número de vacas (cada uma tem 1 cabeça e 4 pés).
Assim, temos:
g + v = 32
2g + 4v = 86
Simplificamos a segunda equação dividindo por 2:
g + 2v = 43
Agora, subtraímos as equações:
(g + 2v) − (g + v) = 43 – 32
g + 2v – g – v = 11
v = 11
Substituímos v = 11 na primeira equação:
g + 11 = 32
g = 32 – 11
g = 21
Há 21 galinhas e 11 vacas.
Em uma corrida com cinco participantes (Heitor, Cárita, Marta, Jorge e Raul), temos as seguintes informações:
1. Cárita chegou logo antes de Jorge.
2. Marta não foi a última.
3. Heitor chegou entre Cárita e Raul.
Pergunta: Quem foi o último colocado?
A) Cárita
B) Marta
C) Jorge
D) Raul
E) Heitor
Alternativa D
Vamos analisar as informações dadas com os novos nomes:
1. Cárita chegou logo antes de Jorge
Isso significa que Cárita e Jorge estão em posições consecutivas, com Cárita imediatamente antes de Jorge. Portanto, Jorge não pode estar na primeira posição.
2. Marta não foi a última
Marta não terminou em último lugar, então podemos excluir essa possibilidade para ela.
3. Heitor chegou entre Cárita e Raul
Como Heitor está entre Cárita e Raul, a ordem desses três deve ser algo como Cárita-Heitor-Raul ou Raul-Heitor-Cárita. Como Jorge chegou logo após Cárita (pela primeira afirmação), a única ordem possível é: Cárita-Heitor-Jorge-Raul.
Agora, as posições ficam assim:
- Marta não está em último lugar, então ela ocupa a primeira posição.
- A ordem completa é: Marta, Cárita, Heitor, Jorge e Raul.
Então, o último colocado é o Raul.
(Enem 2023) As características culturais variam de povo para povo. Há notícias de um povo que possuía formas de contar diferentes das nossas, como indicado no quadrinho a seguir.
Segundo o padrão de contagem indicado na figura, as representações dos numerais cinco e sete, nessa cultura, devem ser, respectivamente,
A) okosa urapum urapum urapum e okosa okosa urapum urapum urapum.
B) okosa okosa urapum e okosa okosa okosa okosa urapum.
C) okosa okosa urapum e okosa okosa okosa urapum.
D) okosa urapum urapum e okosa urapum okosa urapum urapum.
E) okosa okosa urapum e okosa okosa okosa okosa.
Alternativa B
Analisando a imagem, sabemos que okosa corresponde a duas unidades e urapum, a uma unidade, logo, temos que:
Para escrever 5, temos que 5 = 2 + 2 + 1, ou seja, okosa okosa urapum.
Para escrever 7, temos que 7 = 2 + 2 + 2 + 1, ou seja, okosa okosa okosa urapum.
Numa agência telefônica, 2 telefonistas atendem 24 clientes em 4 horas. Mantidas as proporções, 3 telefonistas atendem quantos clientes em 4 horas?
A) 30 clientes
B) 36 clientes
C) 48 clientes
D) 52 clientes
E) 60 clientes
Alternativa B
Se 2 atendentes atendem 24 clientes, então cada atendente atenderá: 24 : 2 = 12 em 4 horas.
Sendo assim, como teremos agora 3 atendentes, então serão 12 ⋅ 3 = 36 clientes atendidos.
(Enem 2020) Um motociclista planeja realizar uma viagem cujo destino fica a 500 km de sua casa. Sua moto consome 5 litros de gasolina para cada 100 km rodados, e o tanque da moto tem capacidade para 22 litros. Pelo mapa, observou que no trajeto da viagem o último posto disponível para reabastecimento, chamado Estrela, fica a 80 km do seu destino. Ele pretende partir com o tanque da moto cheio e planeja fazer somente duas paradas para reabastecimento, uma na ida e outra na volta, ambas no posto Estrela. No reabastecimento para a viagem de ida, deve considerar também combustível suficiente para se deslocar por 200 km do seu destino.
A quantidade mínima de combustível, em litro, que esse motociclista deve reabastecer no posto Estrela na viagem de ida, que seja suficiente para fazer o segundo reabastecimento, é:
A) 13.
B) 14.
C) 17.
D) 18.
E) 21.
Alternativa C
Sabemos que 100 km consomem 5 litros, logo, serão consumidos 100 : 5 = 20 litros/ km.
Para fazer 420 km, é necessário um total de 420 : 20 = 21 litros. A capacidade do tanque é de 22 litros, então 22 – 21 = 1, logo, sobrou 1 litro.
O que nos interessa é o combustível necessário para que ele ande os 80 km restantes, mais 200 km dentro da cidade e os 80 km na volta, ou seja, um total de 360 km.
360 : 20 = 18 litros
Como restou 1 litro, então é necessário que ele abasteça, no mínimo, 18 – 1 = 17 L.
(Enem 2023) Um jovem, no trajeto que usa para ir para a escola, sempre passa por um grande relógio digital que há no centro da sua cidade e compara a hora nele mostrada com a hora que marca o seu relógio de pulso. Ao longo de 30 dias de observação, constata que o seu relógio atrasa 2 minutos, a cada 15 dias, em relação ao do centro da cidade.
Após 90 dias, sem nenhum dos dois relógios receberem ajustes e mantida a mesma parcela de atraso diário, ao ler as marcações de horário dos dois relógios, verificou que o do centro da cidade marcava exatamente 7 horas.
Qual horário marcava seu relógio de pulso nesse instante?
A) 6 h e 48 min
B) 6 h e 54 min
C) 6 h e 58 min
D) 7 h e 06 min
E) 7 h e 12 min
Alternativa A
Sabemos que o relógio do jovem atrasa 2 minutos a cada 15 dias. Para calcular o atraso diário, basta dividir 2 minutos por 15 dias:
2 : 15 = 0,1333... minutos por dia
Transformando em segundos:
0,133.. ⋅60 = 8, ou seja, 8 segundos por dia.
Agora, vamos calcular o atraso total do relógio de pulso após 90 dias. Para isso, multiplicamos o atraso diário pelo número de dias:
0,1333.. ⋅ 90 = 12 minutos
Sabemos que, no final de 90 dias, o relógio do centro da cidade marca 7:00. Como o relógio de pulso está atrasado em 12 minutos, o horário real no relógio de pulso será 12 minutos atrás do horário mostrado pelo relógio da cidade.
Logo, o horário no relógio de pulso será:
7:00 − 0:12= 6:48
Portanto, o relógio de pulso do jovem marcava 6:48 quando o relógio do centro da cidade marcava 7:00.
(Enem 2023) O calendário maia apresenta duas contagens simultâneas de anos, o chamado ano Tzolkim, composto por 260 dias e que determinava o calendário religioso, e o ano Haab, composto por 365 dias e que determinava o calendário agrícola. Um historiador encontrou evidências de que gerações de uma mesma família governaram certa comunidade maia pelo período de 20 ciclos, sendo cada ciclo formado por 52 anos Haab.
Disponível em: www.suapesquisa.com. Acesso em: 20 ago. 2014.
De acordo com as informações fornecidas, durante quantos anos Tzolkim aquela comunidade maia foi governada por tal família?
A) 741
B) 1040
C) 1460
D) 2100
E) 5200
Alternativa C
Sabemos que o ano Haab tem 365 dias. O ciclo de 52 anos Haab é formado por 52 anos de 365 dias cada. Portanto, a duração de um ciclo de 52 anos Haab, em dias, é:
52 × 365 = 18.980 dias
Agora, vamos calcular quantos anos Tzolkim existem em 18.980 dias (a duração de um ciclo de 52 anos Haab). Para isso, basta dividir o número total de dias de um ciclo de 52 anos Haab pela quantidade de dias de um ano Tzolkim, que é de 260 dias:
18.980 : 260 = 73 anos
Como cada ciclo de 52 anos Haab equivale a 73 anos Tzolkim, agora podemos calcular o total de anos Tzolkim para 20 ciclos de 52 anos Haab
20 × 73 = 1460 anos Tzolkim
(Enem 2018) A rosa dos ventos é uma figura que representa oito sentidos, que dividem o círculo em partes iguais.
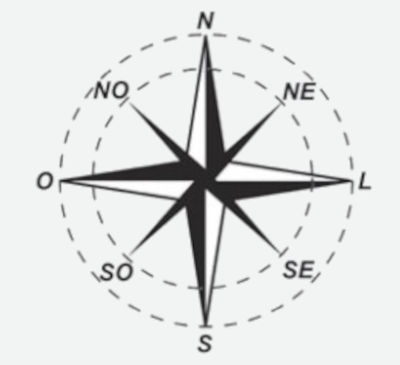
Uma câmera de vigilância está fixada no teto de um shopping, e sua lente pode ser direcionada remotamente, através de um controlador, para qualquer sentido. A lente da câmera está apontada inicialmente no sentido Oeste e o seu controlador efetua três mudanças consecutivas, a saber:
• 1ª mudança: 135° no sentido anti-horário;
• 2ª mudança: 60° no sentido horário;
• 3ª mudança: 45° no sentido anti-horário.
Após a 3ª mudança, ele é orientado a reposicionar a câmera, com a menor amplitude possível, no sentido Noroeste (NO) devido a um movimento suspeito de um cliente.
Qual mudança de sentido o controlador deve efetuar para reposicionar a câmera?
A) 75° no sentido horário.
B) 105° no sentido anti-horário.
C) 120° no sentido anti-horário.
D) 135° no sentido anti-horário.
E) 165° no sentido horário.
Alternativa E
Sabemos que um ângulo inteiro é 360º, e, como ele está dividido em 8 partes, então 360º / 8 = 45º.
- 1ª mudança de 135º vai até SE.
- 2ª mudança de 60º no sentido horário; sabemos que, com 45º, o controle ficará apontado a S, logo, ele ficou a 15º do sul.
- 3ª mudança de 45º no sentido anti-horário; agora, o controle ficará a 30º do sul, no sentido anti-horário.
Note que, nesse caso, o noroeste está a 165º da posição atual da câmera.
(Enem) A imagem apresentada na figura é uma cópia em preto e branco da tela quadrada intitulada O peixe, de Marcos Pinto, que foi colocada em uma parede para exposição e fixada nos pontos A e B.
Por um problema na fixação de um dos pontos, a tela se desprendeu, girando rente à parede. Após o giro, ela ficou posicionada como ilustrado na figura, formando um ângulo de 45° com a linha do horizonte.
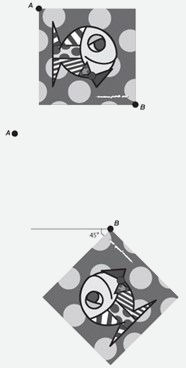
Para recolocar a tela na sua posição original, deve-se girá-la, rente à parede, no menor ângulo possível inferior a 360°. A forma de recolocar a tela na posição original, obedecendo ao que foi estabelecido, é girando-a em um ângulo de
A) 90º no sentido horário.
B) 135º no sentido horário.
C) 180º no sentido anti-horário.
D) 270º no sentido anti-horário.
E) 315º no sentido horário.
Alternativa B
Analisando a imagem, a menor distância para que se retorne à posição original é a rotação de 135º no sentido horário.
(Enem 2018) Um edifício tem a numeração dos andares iniciando no térreo (T), e continuando com primeiro, segundo, terceiro, …, até o último andar. Uma criança entrou no elevador e, tocando no painel, seguiu uma sequência de andares, parando, abrindo e fechando a porta em diversos andares. A partir de onde entrou a criança, o elevador subiu sete andares, em seguida desceu dez, desceu mais treze, subiu nove, desceu quatro e parou no quinto andar, finalizando a sequência. Considere que, no trajeto seguido pela criança, o elevador parou uma vez no último andar do edifício.
De acordo com as informações dadas, o último andar do edifício é o
A) 16º
B) 22º
C) 23º
D) 25º
E) 32º
Alternativa C
Seja x o andar em que a criança está, temos que:
x + 7 - 10 - 13 + 9 - 4 = 5
x = 16
Assim, temos a sequência:
16, 23, 13, 0 = T, 9, 5
Então o último andar é o 23°.
(Enem) Uma loja decide premiar seus clientes. Cada cliente receberá um dos seis possíveis brindes disponíveis, conforme sua ordem de chegada na loja. Os brindes a serem distribuídos são: uma bola, um chaveiro, uma caneta, um refrigerante, um sorvete e um CD, nessa ordem. O primeiro cliente da loja recebe uma bola, o segundo recebe um chaveiro, o terceiro recebe uma caneta, o quarto recebe um refrigerante, o quinto recebe um sorvete, o sexto recebe um CD, o sétimo recebe uma bola, o oitavo recebe um chaveiro, e assim sucessivamente, segundo a ordem dos brindes.
O milésimo cliente receberá de brinde um(a)
A) bola.
B) caneta.
C) refrigerante.
D) sorvete.
E) CD.
Alternativa C
Sabemos que há 6 possibilidades de prêmio e que, a partir do 6º prêmio, o prêmio começa a se repetir; logo, ao dividir 1000 por 6, temos que:
1000 : 6 = 166 com resto 4
Dessa forma, o ciclo se repete 166 vezes e deixa resto 4, ou seja, o 4º prêmio do cliente é um refrigerante.
Uma biblioteca decide organizar seus livros em prateleiras de acordo com a categoria de cada um. Existem 4 categorias de livros: ficção, não ficção, história e ciência. A ordem de organização das prateleiras será: ficção, não ficção, história, ciência, e depois a sequência se repete. A primeira prateleira recebe livros de ficção; a segunda, de não ficção; a terceira, de história; a quarta, de ciência; a quinta, de ficção, e assim por diante.
Considerando essa organização, em que prateleira estará o livro de história de número 11?
A) 3ª prateleira
B) 7ª prateleira
C) 9ª prateleira
D) 11ª prateleira
Alternativa B
Como a sequência se repete a cada 4 prateleiras (ficção, não ficção, história, ciência), o livro de história ocupará sempre as prateleiras que estão na posição 3 de cada ciclo. O 11º livro de história estará na 7ª prateleira, porque 11 dividido por 4 deixa um resto de 3.
Uma escola decide organizar seus alunos em 5 grupos para uma atividade, seguindo uma ordem cíclica. O primeiro grupo recebe o nome de Grupo A; o segundo, de Grupo B; o terceiro, de Grupo C; o quarto, de Grupo D; e o quinto, de Grupo E. A sequência dos grupos se repete de acordo com a ordem de chegada dos alunos, ou seja, o sexto aluno será do Grupo A, o sétimo será do Grupo B, e assim por diante.
Considerando essa organização, qual será o grupo do aluno número 27?
A) Grupo A
B) Grupo B
C) Grupo C
D) Grupo D
E) Grupo E
Alternativa B
A sequência de grupos se repete a cada 5 alunos; então, para descobrir o grupo do aluno 27, basta dividir 27 por 5 e verificar o resto da divisão.
27 : 5 = 5 ciclos completos com resto 2.
O resto 2 significa que o aluno 27 estará na segunda posição do ciclo, que corresponde ao Grupo B.
(Enem) Cinco times de futebol (A, B, C, D e E) ocuparam as primeiras colocações em um campeonato realizado em seu país. A classificação final desses clubes apresentou as seguintes características:
• O time A superou o time C na classificação;
• O time C ficou imediatamente à frente do time E;
• O time B não ficou entre os 3 últimos colocados;
• O time D ficou em uma classificação melhor que a do time A.
Assim, os dois times mais bem classificados foram
A) A e B.
B) A e C.
C) B e D.
D) B e E.
E) C e D.
Alternativa C
Como o time B não terminou entre os três últimos, pode-se concluir que ele ficou nas primeiras posições. Além disso, sabendo que o time A ficou à frente do time C, que, por sua vez, superou o time E, e que o time D ficou à frente do time A, podemos concluir que o time D também ocupa uma das duas primeiras posições.
Então os times que têm a melhor classificação são B e D.
(Enem) Para estimular o raciocínio de sua filha, um pai fez o seguinte desenho e o entregou à criança juntamente com três lápis de cores diferentes. Ele deseja que a menina pinte somente os círculos, de modo que aqueles que estejam ligados por um segmento tenham cores diferentes.
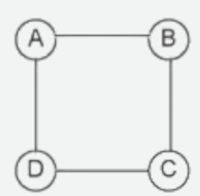
De quantas maneiras diferentes a criança pode fazer o que o pai pediu?
A) 6
B) 12
C) 18
D) 24
E) 72
Alternativa C
Para o círculo A, que não tem nenhuma restrição inicial, temos 3 opções de cores. O círculo B, por ser adjacente ao A, deve ser pintado com uma cor diferente da de A; portanto, há 2 opções de cor para B. O círculo D, adjacente ao B, também deve ser pintado com uma cor diferente da de B; então, ele também tem 2 opções de cor. Por fim, o círculo C, adjacente ao D, deve ser pintado com uma cor diferente da do D, oferecendo-se 2 opções de cor para C.
Existem duas situações:
B e D têm cores diferentes: o número total de possibilidades será o produto das opções para cada círculo: 3 opções para A; 2 para B; 1 para D (já que D é diferente de B); e 1 para C (diferente de D).
3 ⋅ 2 ⋅ 1 ⋅ 1 = 6
B e D têm a mesma cor: temos 3 opções para A, 2 para B, 1 para D (igual a B), e 2 opções para C (diferente de D).
3 ⋅ 2 ⋅ 1 ⋅ 2 = 12
Somando os resultados das duas situações, obtemos um total de 6 + 12 = 18 possibilidades para pintar os círculos de acordo com as restrições.
Portanto, o total de possibilidades de pintar os 4 círculos é 18.
Encontre o próximo número na sequência:
3, 6, 12, 24 ...
A) 30
B) 36
C) 48
D) 54
E) 62
Alternativa C
Note que o termo é sempre o dobro do termo anterior, sendo assim: 24 ⋅ 2 = 48.
Se uma máquina produz 30 peças em 5 horas, quantas peças produzirá em 15 horas mantendo a mesma taxa?
A) 60
B) 75
C) 90
D) 120
E) 150
Alternativa C
A taxa de produção é de 6 peças por hora.
Em 15 horas:
6 ⋅15 = 90
Um tanque é preenchido por 2 mangueiras em 4 horas. Quanto tempo levará para encher com apenas 1 mangueira considerando que ambas têm a mesma vazão?
A) 6 horas
B) 7 horas
C) 8 horas
D) 9 horas
E) 10 horas
Alternativa C
Se duas mangueiras levam 4 horas, uma única mangueira levará o dobro do tempo:
4 × 2 = 8 horas
Se x + y = 10 e x – y = 4, qual é o valor de x?
A) 3
B) 5
C) 7
D) 8
E) 9
Alternativa C
Sabemos que x + y = 10 e que x – y = 4.
Então, temos que:
(x + y) + (x – y) = 10 + 4
2x = 14
x = 14 : 2
x = 7
Quantos números pares existem entre 1 e 20?
A) 16
B) 14
C) 12
D) 10
E) 8
Alternativa D
De 1 até 20, temos 20 números; sendo que metade deles é par, logo, há 10 números pares de 1 até 20.
Ao calcular a divisão de um número por 4, encontramos quociente 6 e resto 2, então podemos afirmar que esse número é igual a?
A) 24
B) 25
C) 26
D) 28
E) 30
Alternativa C
Seja x o número desconhecido, sabemos que x = 6 ⋅ 4 + 2; então, temos que: x = 24 + 2 = 26.
Ana, Bruno e Carla têm idades consecutivas e somam 54 anos. Quantos anos tem Carla, a mais velha?
A) 16
B) 17
C) 18
D) 19
E) 20
Alternativa B
Como as idades são consecutivas, podemos representá-las como x, x + 1, x + 2.
A soma das idades é:
x + (x + 1) + (x + 2) = 54
3x + 3 = 54
3x = 54 – 3
3x = 51
x = 51 : 3
x = 17
Se A é 3 vezes maior que B e a soma de ambos é 20, qual é o valor de B?
A) 4
B) 5
C) 6
D) 7
E) 9
Alternativa B
A = 3B
B + A = 20
B + 3B = 20
4B = 20
B = 20 : 4
B = 5
