Enem: lista de exercícios sobre MMC e MDC
Nesta lista de exercícios, você poderá testar o que aprendeu sobre o mínimo múltiplo comum (MMC) e o máximo divisor comum (MDC), assunto importante para o Enem.
Publicado por: Raul Rodrigues de OliveiraQuestões
-
Questão 1
(Enem 2020) Uma pessoa precisa comprar 15 sacos de cimento para uma reforma em sua casa. Faz pesquisa de preço em cinco depósitos que vendem o cimento de sua preferência e cobram frete para entrega do material, conforme a distância do depósito à sua casa. As informações sobre preço do cimento, valor do frete e distância do depósito até a casa dessa pessoa estão apresentadas no quadro.
Depósito
Valor do saco de cimento
Valor do frete para cada quilômetro
Distância entre a casa e o depósito
(R$)
(R$)
(km)
A
23,00
1,00
10
B
21,50
3,00
12
C
22,00
1,50
14
D
21,00
3,50
18
E
24,00
2,50
2
A pessoa escolherá um desses depósitos para realizar sua compra, considerando os preços do cimento e do frete oferecidos em cada opção.
Se a pessoa decidir pela opção mais econômica, o depósito escolhido para a realização dessa compra será o:
A) A.
B) B.
C) C.
D) D.
E) E.
Alternativa C.
Calculando o valor gasto em cada caso com o produto e o frete, temos que:
A → 15 ∙ 23 + 1 ∙ 10 = 355
B → 15 ∙ 21,50 + 3 ∙ 12 = 358,50
C → 15 ∙ 22 + 1,50 ∙ 14 = 351
D → 15 ∙ 21 + 3,50 ∙ 18 = 378
E → 15 ∙ 24 + 2,50 ∙ 2 = 365
Então, a pessoa escolherá a opção C.
-
Questão 2
(Enem 2020) Pesquisadores da Universidade de Tecnologia de Viena, na Áustria, produziram miniaturas de objetos em impressoras 3D de alta precisão. Ao serem ativadas, tais impressoras lançam feixes de laser sobre um tipo de resina, esculpindo o objeto desejado. O produto final da impressão é uma escultura microscópica de três dimensões, como visto na imagem ampliada.

A escultura apresentada é uma miniatura de um carro de Fórmula 1, com 100 micrômetros de comprimento. Um micrômetro é a milionésima parte de um metro.
Usando notação científica, qual é a representação do comprimento dessa miniatura, em metro?
A) 1,0 x 10-1
B) 1,0 x 10-3
C) 1,0 x 10-4
D) 1,0 x 10-6
E) 1,0 x 10-7
Alternativa C.
Sabemos que 1 micrômetro é igual à milionésima parte de um metro, ou seja:
0,0000001 metro
Como temos 100 micrômetros, então há um total de 0,0001 m. Passando esse número para notação científica, temos: 1 × 10 –4 m.
-
Questão 3
(Enem 2019) Após o Fórum Nacional Contra a Pirataria (FNCP) incluir a linha de autopeças em campanha veiculada contra a falsificação, as agências fiscalizadoras divulgaram que os cinco principais produtos de autopeças falsificados são: rolamento, pastilha de freio, caixa de direção, catalisador e amortecedor.
Disponível em: www.oficinabrasil.com.br. Acesso em: 25 ago. 2014 (adaptado).
Após uma grande apreensão, as peças falsas foram cadastradas utilizando-se a codificação:
1: rolamento, 2: pastilha de freio, 3: caixa de direção, 4: catalisador e 5: amortecedor.
Ao final obteve-se a sequência:
5, 4, 3, 2, 1, 2, 3, 4, 5, 4, 3, 2, 1, 2, 3, 4, 5, 4, 3, 2, 1, 2, 3, 4, … que apresenta um padrão de formação que consiste na repetição de um bloco de números. Essa sequência descreve a ordem em que os produtos apreendidos foram cadastrados.
O 2015º item cadastrado foi um(a):
a) rolamento.
b) catalisador.
c) amortecedor.
d) pastilha de freio
e) caixa de direção.
Alternativa E.
Analisando a sequência, percebemos que ela é cíclica e que cada ciclo possui 8 números (5,4,3,2,1,2,3,4).
Dividindo 2015 por 8, temos como quociente 251. Isso significa que a sequência se repetiu 251 vezes e, além disso, o resto é 7, logo a sequência se repetiu até o 7º termo, que é 3. Sendo assim, o 2015° produto cadastrado foi o 3 — caixa de direção.
-
Questão 4
(Enem 2017) Uma pessoa ganhou uma pulseira formada por pérolas esféricas, na qual faltava uma das pérolas. A figura indica a posição em que estaria faltando esta pérola.

Ela levou a joia a um joalheiro que verificou que a medida do diâmetro dessas pérolas era 4 milímetros. Em seu estoque, as pérolas do mesmo tipo e formato, disponíveis para reposição, tinham diâmetros iguais a: 4,025 mm; 4100 mm; 3970 mm; 4,080 mm; e 3,099 mm O joalheiro então colocou na pulseira a pérola cujo diâmetro era o mais próximo do diâmetro das pérolas originais.
A pérola colocada na pulseira pelo joalheiro tem diâmetro, em milímetro, igual a:
A) 3,099
B) 3,970
C) 4,025
D) 4,080
E) 4,100
Alternativa C.
Calculando a diferença entre o diâmetro de cada uma delas e 4,000, temos que:
4,025 – 4,000 = 0,025
4,000 – 3,970 = 0,030
4,000 – 3,099 = 0,901
4,080 – 4,000= 0,080
4,100 – 4,000=0,100
A que possui valor mais próximo de 4,000 é a que tem diâmetro de 4,025.
-
Questão 5
(Enem 2016) O ábaco é um antigo instrumento de cálculo que usa notação posicional de base dez para representar números naturais. Ele pode ser apresentado em vários modelos, um deles é formado por hastes apoiadas em uma base. Cada haste corresponde a uma posição no sistema decimal e nelas são colocadas argolas; a quantidade de argolas na haste representa o algarismo daquela posição. Em geral, colocam-se adesivos abaixo das hastes com os símbolos U, D, C, M, DM e CM que correspondem, respectivamente, a unidades, dezenas, centenas, unidades de milhar, dezenas de milhar e centenas de milhar, sempre começando com a unidade na haste da direita e as demais ordens do número no sistema decimal nas hastes subsequentes (da direita para esquerda), até a haste que se encontra mais à esquerda.
Entretanto, no ábaco da figura, os adesivos não seguiram a disposição usual.
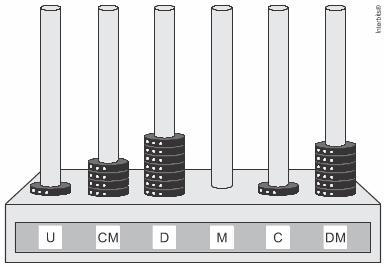
Nessa disposição, o número que está representado na figura é:
A) 46 171.
B) 147 016.
C) 171 064.
D) 460 171.
E) 610 741.
Alternativa D.
Pela legenda, é possível perceber que a ordem está diferente da que utilizamos, pois nesse caso seria CM → DM → M → C → D → U.
-
Centenas de milhar → CM → 4
-
Dezenas de milhar → DM → 6
-
Milhar → M → 0
-
Centena → C → 1
-
Dezena → D → 7
-
Unidade → U → 1
O número representado é o 460 171.
-
-
Questão 6
(Enem 2015) O gerente de um cinema fornece anualmente ingressos gratuitos para escolas. Este ano, serão distribuídos 400 ingressos para uma sessão vespertina e 320 ingressos para uma sessão noturna de um mesmo filme. Várias escolas podem ser escolhidas para receberem ingressos. Há alguns critérios para a distribuição dos ingressos:
1) cada escola deverá receber ingressos para uma única sessão;
2) todas as escolas contempladas deverão receber o mesmo número de ingressos;
3) não haverá sobra de ingressos (ou seja, todos os ingressos serão distribuídos).
O número mínimo de escolas que podem ser escolhidas para obter ingressos, segundo os critérios estabelecidos, é:
A) 2
B) 4
C) 9
D) 40
E) 80
-
Questão 7
(Enem 2015) Um arquiteto está reformando uma casa. De modo a contribuir com o meio ambiente, decide reaproveitar tábuas de madeira retiradas da casa. Ele dispõe de 40 tábuas de 540 cm, 30 de 810 cm e 10 de 1.080 cm, todas de mesma largura e espessura. Ele pediu a um carpinteiro que cortasse as tábuas em pedaços de mesmo comprimento, sem deixar sobras, e de modo que as novas peças ficassem com o maior tamanho possível, mas de comprimento menor que 2 m.
Atendendo ao pedido do arquiteto, o carpinteiro deverá produzir:
A) 105 peças.
B) 120 peças.
C) 210 peças.
D) 243 peças.
E) 420 peças.
Alternativa E.
Calcularemos o MDC entre 540, 810 e 1080:
540 = 2 · 3³ · 5
810 = 34 · 2 · 5
1080 = 2² · 3³ · 5
MDC (540, 810, 1080) = 3³ · 2 · 5 = 270
Mas as peças não podem ter 270 cm. O maior divisor de 270 é 135, então cada peça deve ter
135 cm:
(40 · 540 + 30 · 810 + 10 · 1080) : 135 = 420 peças
-
Questão 8
(Enem 2012) João decidiu contratar os serviços de uma empresa por telefone através do SAC (Serviço de Atendimento ao Consumidor). O atendente ditou para João o número de protocolo de atendimento da ligação e pediu que ele anotasse. Entretanto, João não entendeu um dos algarismos ditados pelo atendente e anotou o número 13_98207 sendo que o espaço vazio é o do algarismo que João não entendeu.
De acordo com essas informações, a posição ocupada pelo algarismo que falta no número de protocolo é a de:
A) centena.
B) dezena de milhar.
C) centena de milhar.
D) milhão.
E) centena de milhão.
Alternativa C.
A posição ocupada pelo número é a de centena de milhar.
-
Questão 9
(FMJ 2021) Um grupo de 4 nadadores atravessa uma piscina, que tem 20 m de um lado a outro, com tempos individuais de 12 s, 15 s, 18 s e 25 s. Esses atletas iniciaram um treino, de um mesmo lado da piscina, atravessando-a de um lado para outro continuamente. Quando chegam a um lado da piscina, eles imediatamente passam a nadar em direção ao lado oposto. A primeira vez em que os quatro nadadores chegarem, ao mesmo tempo, em um mesmo lado da piscina, o nadador mais rápido terá nadado um total de:
A) 1.000 m.
B) 2.000 m.
C) 2.500 m.
D) 1.500 m.
E) 3.000 m.
Alternativa D.
Queremos encontrar o MMC entre 12, 15, 18 e 25.Sabemos que:
12 = 2² · 3
15 = 3 ·5
18 = 2 ·3²
25 = 5²
Então, o MMC (12, 15, 18, 25) = 2² ·3²- · 5² = 900 segundos.
Se o nadador mais rápido nada 20 metros a cada 12 segundos, temos que:
900 : 12 = 75 voltas e 75 · 20 = 1500 metros
-
Questão 10
(Uerj 2020) Uma gerente de loja e seu assistente viajam com frequência para São Paulo e voltam no mesmo dia. A gerente viaja a cada 24 dias e o assistente, a cada 16 dias, regularmente. Em um final de semana, eles viajaram juntos. Depois de x viagens da gerente e y viagens do assistente sozinhos, eles viajaram juntos novamente.
O menor valor de x + y é:
A) 1
B) 2
C) 3
D) 4
Alternativa C.
Calculando o MMC (16, 24), temos que:
16 = 24
24 = 3 · 2³
MMC(16, 24) = 24 · 3 = 48
Logo, eles viajam juntos a cada 48 dias. A gerente viajou sozinha no dia 24 (x = 1), e o assistente, nos dias 16 e 32 (y = 2).
x + y = 1 + 2 = 3
-
Questão 11
(Famema 2020) Sílvia e Márcio moram em cidades diferentes no interior. Sílvia vai à capital uma vez a cada 10 dias, e Márcio vai à capital uma vez a cada 12 dias. A última vez em que eles se encontraram na capital foi um sábado. O próximo encontro dos dois na capital ocorrerá em:
A) uma terça-feira.
B) uma quarta-feira.
C) um domingo.
D) um sábado.
E) uma segunda-feira.
Alternativa B.
Calculando o MMC entre 10 e 12, temos que:
10 = 2 · 5
12 = 2² · 3
MMC (10, 12) = 2² · 3 · 5 = 60.
60 dias correspondem a 8 semanas e 4 dias.
A partir de sábado, o 4º dia é a quarta-feira.
-
Questão 12
(IF-MT 2020) João decide reformar sua casa, mas, como não dispõe de muito dinheiro, decide economizar na reforma contratando o carpinteiro José para reaproveitar as tábuas de madeira retiradas da casa. José tem à sua disposição 40 tábuas de 5,4 metros, 30 tábuas de 8,10 metros e 10 tábuas de 10,80 metros, todas de mesma espessura e largura. Para atender às especificidades da reforma da casa de João, José decide cortar as tábuas em pedaços de mesmo comprimento, sem deixar sobras, e de modo que as novas peças fiquem com o maior tamanho possível, mas de comprimento menor que 2 metros. Qual a quantidade de tábuas que José conseguiu produzir?
A) 395 tábuas
B) 399 tábuas
C) 412 tábuas
D) 420 tábuas
E) 429 tábuas
Alternativa D.
Transformaremos as medidas para centímetros para encontrar o MDC.
Calcularemos o MDC entre 540 cm, 810 cm e 1080 cm:
540 = 2 · 3³ · 5
810 = 34 · 2 · 5
1080 = 2² · 3³ · 5
MDC (540, 810, 1080) = 3³ · 2 · 5 = 270 (em metros, equivalem a 2,7 metros)
Como o valor máximo de cada peça é de 2 metros, é necessário pegar o maior divisor de 2,7 : 2 = 1,35 metro.
Logo:
-
5,4: 1,35 = 4 pedaços
-
8,1 : 1,35= 6 pedaços
-
10,8 : 1,35= 8 pedaços
Multiplicando os pedaços pela quantidade de tábuas, temos que:
4 · 40 = 160
6 · 30 = 180
8 · 10 = 80
A soma 160 + 180 + 80 = 420 tábuas.
-
-
Questão 13
(CMRJ 2020) A direção do Colégio Militar do Rio de Janeiro contratou uma empresa com o objetivo de construir uma nova sala para o Clube Literário. A sala terá 3,36 m de largura e 4,00 m de comprimento. No piso, o pedreiro vai colocar peças de cerâmica quadradas, do mesmo tamanho.
Admitindo-se que não haverá perda de material, a menor quantidade dessas peças que ele vai usar para cobrir completamente o piso é um número:
A) ímpar e menor que 500.
B) múltiplo de 10.
C) maior que 570.
D) igual a 525.
E) primo.
Alternativa D.
Transformando em cm, são 400 cm de comprimento e 336 cm de largura. Calculando o MDC entre esses números, temos que:
400 = 24 · 5
336 = 24 · 3 · 7MDC ( 400, 336) = 24 = 16
400 : 16 = 25 cm de comprimento
336 : 16 = 21 cm de largura25 · 21 = 525
-
Questão 14
(Enem Digital 2020) Um jogo pedagógico é formado por cartas nas quais está impressa uma fração em uma de suas faces. Cada jogador recebe quatro cartas e vence aquele que primeiro consegue ordenar crescentemente suas cartas pelas respectivas frações impressas. O vencedor foi o aluno que recebeu as cartas com as frações:
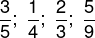
A ordem que esse aluno apresentou foi:
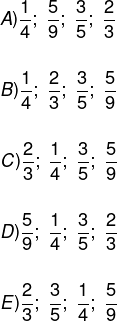
Alternativa A.
A alternativa que apresenta a ordem crescente dessas frações é a alternativa A.
-
Questão 15
(IF-CE 2020) Um relógio A bate a cada 15 minutos, outro relógio B bate a cada 20 minutos, e um terceiro relógio C, a cada 25 minutos. O menor intervalo de tempo decorrido entre duas batidas simultâneas dos três relógios, em horas, é igual a:
A) 3
B) 6
C) 4
D) 5
Alternativa D.
Primeiro encontraremos o MMC entre 15, 20 e 25:
15 = 3 · 5
20 = 2² · 5
25 = 5²
MMC (15, 20, 25) = 3 · 2² · 5² = 300 minutos.
Como a questão pediu o tempo em horas, sabemos que 300 : 60 = 5 horas.