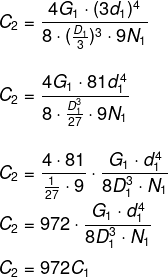Enem: lista de exercícios sobre razão e proporção
Com esta lista de exercícios, você poderá testar suas habilidades em realizar cálculos envolvendo razão e proporção, tema importantíssimo para o Enem.
Publicado por: Raul Rodrigues de OliveiraQuestões
-
Questão 1
(Enem 2020) Uma torneira está gotejando água em um balde com capacidade de 18 litros. No instante atual, o balde se encontra com ocupação de 50% de sua capacidade. A cada segundo caem 5 gotas de água da torneira, e uma gota é formada, em média, por 5×10-2 ml de água. Quanto tempo, em hora, será necessário para encher completamente o balde, partindo do instante atual?
A) 2 × 10¹
B) 1 × 10¹
C) 2 × 10–2
D) 1 × 10-- 2
E) 1 × 10 – 3
Alternativa B.
Como a capacidade do balde é de 18 litros e 50% dele está ocupado, sabemos que:
50% de 18 = 0,5 × 18 = 9 litros
9 litros = 9 000 ml
Sabemos que cada gota possui 5×10-2 ml = 0,05 ml cada. Como a cada segundo há 5 gotas, então é um total de 0,25 ml por segundo.
Logo será necessário um total de 9000 : 0,25 = 36000 segundos para preencher as 9000 ml restantes.
Sabemos que 3600 segundos correspondem a 10 horas, que, em notação científica, é igual a 1×10¹.
-
Questão 2
(Enem 2020) Um motociclista planeja realizar uma viagem cujo destino fica a 500 km de sua casa. Sua moto consome 5 litros de gasolina para cada 100 km rodados, e o tanque da moto tem capacidade para 22 litros. Pelo mapa, observou que no trajeto da viagem o último posto disponível para reabastecimento, chamado Estrela, fica a 80 km do seu destino. Ele pretende partir com o tanque da moto cheio e planeja fazer somente duas paradas para reabastecimento, uma na ida e outra na volta, ambas no posto Estrela. No reabastecimento para a viagem de ida, deve considerar também combustível suficiente para se deslocar por no 200 km seu destino.
A quantidade mínima de combustível, em litro, que esse motociclista deve reabastecer no posto Estrela na viagem de ida, que seja suficiente para fazer o segundo reabastecimento, é:
A) 13.
B) 14.
C) 17.
D) 18.
E) 21.
Alternativa C.
Sabemos que 100 km consomem 5 litros, logo serão consumidos 100 : 5 = 20 litros/ km.
Para fazer 420 km, é necessário um total de 420 : 20 = 21 litros. A capacidade do tanque é de 22 litros, então 22 – 21 = 1, logo sobrou 1 litro.
O que nos interessa é o combustível necessário para que ele ande os 80 km restantes, mais 200 km dentro da cidade e os 80 km na volta, ou seja, um total de 360 km.
360 : 20 = 18 litros
Como restou 1 litro, então é necessário que ele abasteça, no mínimo, 18 – 1 = 17 L.
-
Questão 3
(Enem 2020) Uma empresa de ônibus utiliza um sistema de vendas de passagens que fornece a imagem de todos os assentos do ônibus, diferenciando os assentos já vendidos, por uma cor mais escura, dos assentos ainda disponíveis. A empresa monitora, permanentemente, o número de assentos já vendidos e compara-o com o número total de assentos do ônibus para avaliar a necessidade de alocação de veículos extras.
Na imagem tem-se a informação dos assentos já vendidos e dos ainda disponíveis em um determinado instante.
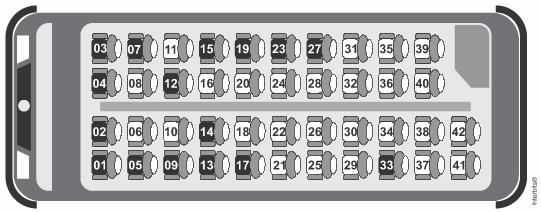
A razão entre o número de assentos já vendidos e o total de assentos desse ônibus, no instante considerado na imagem, é:
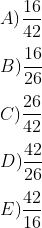
Alternativa A.
Sabemos que há um total de 16 assentos vendidos entre os 42 acentos, logo a razão entre o número de acentos vendidos em relação ao total de acentos do ônibus é de 16/42.
-
Questão 4
(Enem 2019) Para contratar três máquinas que farão o reparo de vias rurais de um município, a prefeitura elaborou um edital que, entre outras cláusulas, previa:
-
cada empresa interessada só pode cadastrar uma única máquina para concorrer ao edital;
-
o total de recursos destinados para contratar o conjunto das três máquinas é de R$ 31.000,00;
-
o valor a ser pago a cada empresa será inversamente proporcional à idade de uso da máquina cadastrada pela empresa para o presente edital.
As três empresas vencedoras do edital cadastraram máquinas com 2, 3 e 5 anos de idade de uso.
Quanto receberá a empresa que cadastrou a máquina com maior idade de uso?
A) R$ 3.100,00
B) R$ 6.000,00
C) R$ 6.200,00
D) R$ 15.000,00
E) R$ 15.500,00
Alternativa B.
Cada empresa receberá de forma inversamente proporcional ao tempo de uso da máquina, então sejam x, y, z correspondentes ao recebimento de cada empresa, temos que:
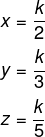
Sabemos que a soma x + y + z = 31.000, logo:
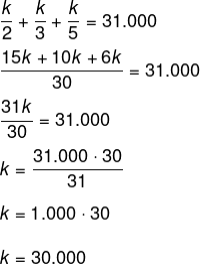
Conhecendo o valor de k, a empresa que tem maior idade é a de 5 anos, então basta calcular k dividido por 5:
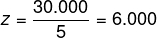
-
-
Questão 5
(Enem 2019) Os exercícios físicos são recomendados para o bom funcionamento do organismo, pois aceleram o metabolismo e, em consequência, elevam o consumo de calorias. No gráfico, estão registrados os valores calóricos, em kcal, gastos em cinco diferentes atividades físicas, em função do tempo dedicado às atividades, contado em minuto.
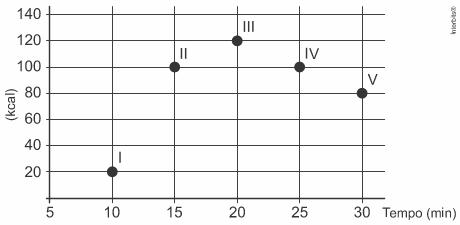
Qual dessas atividades físicas proporciona o maior consumo de quilocalorias por minuto?
A) I
B) II
C) III
D) IV
E) V
Alternativa B.
Para encontrar a atividade física que proporciona maior consumo, basta calcular a razão entre o valor calórico e o tempo:
I → 20 : 10 = 2kcal/min
II → 100 : 15 = 6,6 kcal/min
III → 120 : 20 = 6 kcal/min
IV → 100 : 2,5 = 4kcal/min
V → 80 : 30 = 2,66 kcal/min
Comparando as atividades, a que possui maior consumo calórico por minuto é a atividade II.
-
Questão 6
(Enem 2018) De acordo com a Lei Universal da Gravitação, proposta por Isaac Newton, a intensidade da força gravitacional F que a Terra exerce sobre um satélite em órbita circular é proporcional à massa m do satélite e inversamente proporcional ao quadrado do raio r da órbita, ou seja:
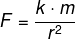
No plano cartesiano, três satélites, A, B e C estão representados, cada um, por um ponto (m,r) cujas coordenadas são, respectivamente, a massa do satélite e o raio da sua órbita em torno da Terra.
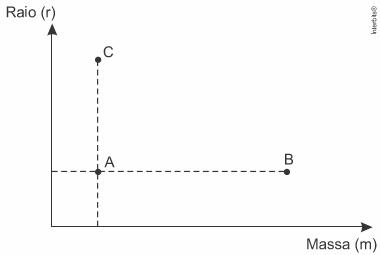
Com base nas posições relativas dos pontos no gráfico, deseja-se comparar as intensidades FA, FB e FC da força gravitacional que a Terra exerce sobre os satélites A, B e C respectivamente.
As intensidades FA, FB e FC expressas no gráfico satisfazem a relação:
A) FC = FA < FB
B) FA = FB < FC
C) FA < FB < FC
D) FA < FC < FB
E) FC < FA < FB
Alternativa E.
Ao comparar A e C, sabemos que eles possuem mesma massa, mas que o raio do C é maior que o raio do A. Calculamos a força gravitacional pela fórmula:
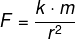
Como o raio de C é maior, então Fc < FA.
Agora, comparando A e B, sabemos que eles possuem mesmo raio, mas que a massa de B é maior que a massa de A, o que faz com que FA < FB.
Então, temos que FC < FA < FB.
-
Questão 7
(Enem 2017) O resultado de uma pesquisa eleitoral, sobre a preferência dos eleitores em relação a dois candidatos, foi representado por meio do Gráfico 1.
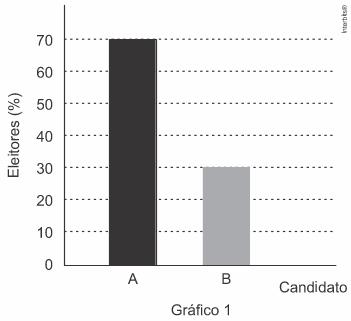
Ao ser divulgado esse resultado em jornal, o Gráfico 1 foi cortado durante a diagramação, como mostra o Gráfico 2.
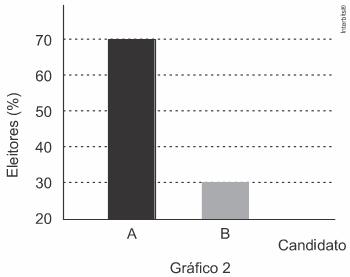
Apesar de os valores apresentados estarem corretos e a largura das colunas ser a mesma, muitos leitores criticaram o formato do Gráfico 2 impresso no jornal, alegando que houve prejuízo visual para o candidato B.
A diferença entre as razões da altura da coluna B pela coluna A nos gráficos 1 e 2 é:
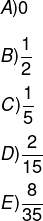
Alternativa E
No primeiro gráfico, a barra maior ocupa 7 linhas e a menor 3, logo elas estão em uma razão de 3/7. Já no segundo gráfico, a razão é de 1/5, então, calculando a diferença, temos que:
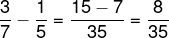
-
Questão 8
(Enem 2016) Para a construção de isolamento acústico numa parede cuja área mede 9 m², sabe-se que, se a fonte sonora estiver a 3 m do plano da parede, o custo é de R$ 500,00. Nesse tipo de isolamento, a espessura do material que reveste a parede é inversamente proporcional ao quadrado da distância até a fonte sonora, e o custo é diretamente proporcional ao volume do material do revestimento.
Uma expressão que fornece o custo para revestir uma parede de área A (em metro quadrado), situada a D metros da fonte sonora, é:
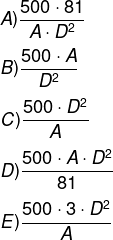
Alternativa B.
Seja E a espessura do material, sabemos que a multiplicação da espessura pela área é igual ao volume, ou seja: E · A = V.
Sabemos que a espessura E é inversamente proporcional ao quadrado da distância D² e que o custo C é diretamente proporcional ao volume E · A, então temos que:
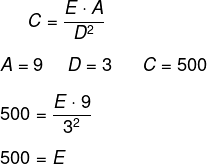
Encontrando o valor de E, temos que:
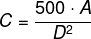
-
Questão 9
(Enem 2016) No tanque de um certo carro de passeio cabem até 50L de combustível, e o rendimento médio deste carro na estrada é de 15 km/L de combustível. Ao sair para uma viagem de 600 km, o motorista observou que o marcador de combustível estava exatamente sobre uma das marcas da escala divisória do medidor, conforme figura a seguir.
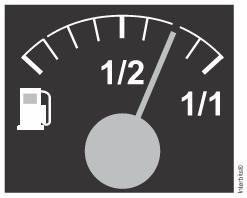
Como o motorista conhece o percurso, sabe que existem, até a chegada a seu destino, cinco postos de abastecimento de combustível, localizados a 150 km, 187 km, 450 km, 500 km e 570 km do ponto de partida.
Qual a máxima distância, em quilômetro, que poderá percorrer até ser necessário reabastecer o veículo, de modo a não ficar sem combustível na estrada?
A) 570
B) 500
C) 450
D) 187
E) 150
Alternativa B.
O marcador de consumo de combustível indica que foram gastos 1/4 do combustível, logo resta 3/4. Como no tanque cabem 50 litros e o automóvel faz 15 km/L, com um tanque, é possível percorrer 50 · 15 = 750 km. Agora basta calcular 3/4 de 750:
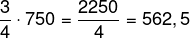
-
Questão 10
(Enem 2014) Diariamente, uma residência consome 20.160Wh. Essa residência possui 100 células solares retangulares (dispositivos capazes de converter a luz solar em energia elétrica) de dimensões 6 cm x 8 cm. Cada uma das tais células produz, ao longo do dia, 24Wh por centímetro de diagonal. O proprietário dessa residência quer produzir, por dia, exatamente a mesma quantidade de energia que sua casa consome.
Qual deve ser a ação desse proprietário para que ele atinja o seu objetivo?
A) Retirar 16 células.
B) Retirar 40 células.
C) Acrescentar 5 células.
D) Acrescentar 20 células.
E) Acrescentar 40 células.
Alternativa A.
Para calcular a diagonal de cada célula retangular, aplicamos o teorema de Pitágoras:
d² = 6² + 8²
d² = 36 + 64
d² = 100
d = √100
d = 10
Então, cada célula produz 10 · 24 = 240 Wh. Como há 100 células, logo será produzido o total de 100 · 240 = 24000 Wh.
O consumo a mais será de 24000 – 21160 = 3840 Wh, então temos que 3840 : 240 = 16, logo é necessário retirar 16 células.
-
Questão 11
(Unicamp 2021) Duas impressoras funcionando simultaneamente imprimem certa quantidade de páginas em 36 segundos. Sozinha, uma delas imprime a mesma quantidade de páginas em 90 segundos. Funcionando sozinha, para imprimir a mesma quantidade de páginas, a outra impressora gastaria:
A) 48 segundos.
B) 54 segundos.
C) 60 segundos.
D) 72 segundos.
Alternativa C.
Sabemos que a primeira gasta 90 segundos, e a segunda gastará sozinha t segundos:
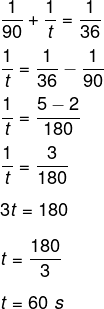
-
Questão 12
(FGV 2021) Em 8 horas diárias de trabalho, 20 caminhões carregam 160 m³ de terra em 15 dias. Se o empreiteiro da obra deseja aumentar a frota em 4 caminhões para realizar o mesmo serviço em 6 dias, o número diário de horas que os caminhões terão que trabalhar para cumprir o novo prazo é de:
A) 16 horas e 40 minutos.
B) 16 horas e 33 minutos.
C) 15 horas e 50 minutos.
D) 15 horas e 45 minutos.
E) 15 horas e 30 minutos.
Alternativa A.
Se cada caminhão trabalhou 8 horas por dia durante 15 dias, então o tempo trabalhado foi de 8 ·15 = 120 horas. Na segunda situação, o tempo trabalhado é igual a 6 vezes o número de dias (d).
Montando a regra de três, temos que:
Tempo
Caminhões
120
20
6d
24
Sabemos que tempo e quantidade de caminhões são inversamente proporcionais, pois, se aumentarmos o número de caminhões, o tempo necessário para fazer o serviço será menor. Multiplicando reto, temos que:
6d · 24 = 120 · 20
144d = 2400
d = 2400 : 144
d = 16,66…
Sabemos que serão gastos 16 horas e 0,666... de uma hora. Como 1 hora possui 60 minutos, então 60 · 0,6666… = 40 minutos. Serão gastos 16 horas e 40 minutos.
-
Questão 13
(IFSC 2020) Na secretaria acadêmica de um campus do IFSC, no dia da matrícula dos alunos, 3 (três) colaboradores atenderam 80 (oitenta) alunos em 4 (quatro) horas.
Se houvesse 4 (quatro) colaboradores atendendo os alunos no mesmo ritmo, quantas horas eles levariam para atender 160 (cento e sessenta) alunos?
Assinale a alternativa CORRETA.
A) 3 (três) horas
B) 5 (cinco) horas
C) 6 (seis) horas
D) 8 (oito) horas
E) 9 (nove) horas
Alternativa A.
Sabemos que 3 colaboradores atenderam 80 estudantes em 4 horas. Queremos saber quanto tempo 4 colaboradores gastarão para atender 160 estudantes. Montando a tabela, temos que:
Tempo
Colaboradores
Estudantes
4 horas
3
80
x horas
4
160
Sabemos que tempo e quantidade de colaboradores é inversamente proporcional, pois, se aumentarmos a quantidade de colaboradores, o tempo gasto para os atendimentos será menor.
Já tempo e estudantes é diretamente proporcional, pois, se o tempo for maior, o número de estudantes atendidos será maior. Então, montando a regra de três:
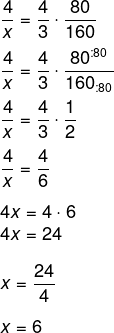
-
Questão 14
(Fatec 2020) Douglas, aluno do curso de Instalações Elétricas, sabe que a resistência elétrica de um fio é diretamente proporcional ao seu comprimento e inversamente proporcional ao quadrado do diâmetro de sua secção transversal. Durante uma atividade prática do curso, Douglas precisou realizar uma melhoria em uma máquina. Para isso um fio deveria ser trocado por outro do mesmo material, mas cujo
- comprimento seria 60 % maior; e
- diâmetro seria 20 % menor.
Assinale a alternativa que apresenta corretamente a relação entre a resistência do fio retirado (R1) e a resistência do novo fio (R2).
A) R2 = 0,20 · R1
B) R2 = 0,30 · R1
C) R2 = 0,75 · R1
D) R2 = 1,50 · R1
E) R2 = 2,50 ·R1
Alternativa E.
Existe uma constante k tal que:
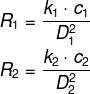
Por outro lado, sabemos que:
-
c2 = 1,6c1 (60%) maior;
-
d2 = 0,8d1 (20%) menor.
Então, temos que:
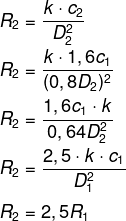
-
-
Questão 15
(CP1 2020) O Colégio Pedro II disponibilizou diversas salas de aula em seus campi para aplicação das provas do concurso de estudantes deste ano. Para arrumar tais salas, seis pessoas trabalharam por três dias.
Para que a mesma quantidade total de salas de aula ficasse pronta em um único dia, o número de pessoas a mais que teriam que ajudar na arrumação, trabalhando no mesmo ritmo das anteriores, é de:
A) 10
B) 12
C) 16
D) 18
Alternativa B.
Sabemos que 6 pessoas levam 3 dias. Para que leve apenas 1 dia, basta triplicar a equipe, ou seja, 18 pessoas levam 1 dia para realizar esse trabalho. Como o enunciado pede para encontrar quantas pessoas a mais, devem ser contratadas, então: 18 – 6 = 12.
-
Questão 16
(IFSUL 2020) Atualmente, no Brasil, muitas escolas vêm implementando uma proposta bilíngue na educação dos surdos, ou seja, o aprendizado da Libras e da Língua Portuguesa escrita como segunda língua. Isto tem sido o resultado de lutas dos surdos brasileiros por uma educação que atenda de forma eficaz suas necessidades linguísticas e culturais.
Disponível em: <https://www.webartigos.com/artigos/a-importancia-do-ensino-da-libras-lingua-brasileira-de-sinais-nas-escolas-de-ensino-fundamental/25014/>. Acesso em 25 ago. 2019.
Considerando uma escola com 1500 alunos, dos quais 33% sabem português e Libras e o restante sabe somente português, o número de estudantes que devem ingressar nessa escola, sabendo português e LIBRAS, de forma que 45% dos estudantes saibam os dois idiomas é de, aproximadamente:
A) 1005
B) 822
C) 495
D) 327
Alternativa D.
Sabemos que, dos 1500 estudantes, 33% sabem libras e português, então: 1500 · 0,33 = 495.
x + 495 = 0,45 (1500 + x)
x + 33 = 675 + 0,45x
x – 0,45x = 675 – 495
0,55x = 180
x = 180 : 0,55
x = 327
-
Questão 17
(CFTMG 2020) Paula produziu 3000 bombons, trabalhando de segunda a sábado durante 6 horas em cada um desses dias. Dias depois, ela recebeu uma nova encomenda urgente de 4.000 bombons gourmet, dos mesmos produzidos anteriormente, para entregá-los em, no máximo, três dias de trabalho. Diante dessa nova encomenda, Paula chamou duas ajudantes doceiras com o seu mesmo rendimento nesse trabalho de produzir seus bombons. As três se dispuseram a trabalhar oito horas por dia para entregar a encomenda.
Nessas condições, calculando o número de dias gastos para concluir a encomenda, pode-se afirmar, corretamente, que as três:
A) produzirão os 4.000 bombons com dois dias de trabalho.
B) produzirão os 4.000 bombons com três dias de trabalho.
C) não entregarão a encomenda, pois necessitam de quatro dias de trabalho para a produção dos 4.000 bombons.
D) não entregarão a encomenda, pois necessitam de cinco dias de trabalho para a produção dos 4.000 bombons.
Alternativa A.
Para encontrar o número de dias gastos, sabemos que a Sara, sozinha, trabalhando 6 horas durante 6 dias, ou seja, 36 horas, produziu 3000 bombons.
Seja d o número de dias trabalhados, sabemos que 3 pessoas trabalhando 8 horas por dia, ou seja, um total de 8d em horas, produziram 4000 bombons.
Sabemos que tempo e quantidade de pessoas é inversamente proporcional, e tempo e quantidade de bombons é diretamente proporcional. Então, podemos chegar à seguinte relação:
Tempo
Quantidade de pessoas
Quantidade de bombons
360 horas
1
3000
8d
3
4000
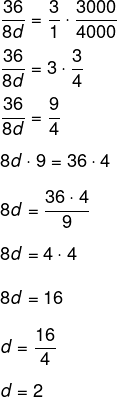
-
Questão 18
(IFMT 2020) Em um incêndio de grandes proporções, foram chamados 30 bombeiros para realizar o rescaldo numa área de 200 m². Considerando que esses bombeiros demoraram 96 horas para controlar as chamas, quantos bombeiros teriam sido necessários para controlar as chamas em 60 horas?
A) 35
B) 37
C) 48
D) 50
E) 52
Alternativa C.
As grandezas são: quantidade de bombeiros e tempo gasto. Sabemos que, quanto maior a quantidade de bombeiros, menor será o tempo gasto, logo essas grandezas são inversamente proporcionais.
Quantidade de bombeiros
Tempo gasto
30
96
x
60
Como as grandezas são inversamente proporcionais, multiplicaremos reto:
60x = 30 · 96
60x = 2880
x = 2880 : 60
x = 48
-
Questão 19
(IFPE 2019) O Homem-Escorpião, o Menino-Vespa e a Garota-Abelha já derrotaram, juntos, 600 vilões na proporção 13, 2 e 5, respectivamente. Quantos vilões o Homem-Escorpião derrotou a mais que o Menino-Vespa?
A) 240 vilões.
B) 330 vilões.
C) 90 vilões.
D) 360 vilões.
E) 210 vilões.
Alternativa B.
Seja k a constante de proporção, sabemos que:
-
número de vilões derrotados pelo Homem-Escorpião = 13k
-
número de vilões derrotados pelo Menino-Vespa = 2k
-
número de vilões derrotados pela Garota-Abelha = 5k
E a soma:
13k + 2k + 5k = 600
20k = 600
k = 600 : 20
k = 30
Agora, para encontrar o número de vilões derrotados pelo Homem-Escorpião, temos que:
13 · 30 = 390
Já o número de vilões derrotados pelo Menino-Vespa é dado por:
2 · 30 = 60
Então, a diferença foi de 390 – 60 = 330 vilões.
-
-
Questão 20
(Enem PPL 2019) Para certas molas, a constante elástica (C) depende do diâmetro médio da circunferência da mola (D), do número de espirais úteis (N), do diâmetro (d) do fio de metal do qual é formada a mola e do módulo de elasticidade do material (G), A fórmula evidencia essas relações de dependência.
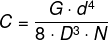
O dono de uma fábrica possui uma mola M1 em um de seus equipamentos, que tem características D1, N1, d1 e G1 com uma constante elástica C1. Essa mola precisa ser substituída por outra, M2, produzida com outro material e com características diferentes, bem como uma nova constante elástica C2, da seguinte maneira:
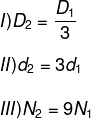
Além disso, a constante de elasticidade G2 do novo material é igual a 4G1.
O valor da constante C2 em função da constante C1 é:
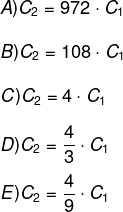
Alternativa A.
O valor de C1 é representado pela expressão:
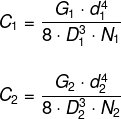
Substituindo em C2 os valores representados em I, II e III, temos que: