Enem: lista de exercícios sobre regra de três simples e composta
Com esta lista de exercícios, você poderá testar suas habilidades em lidar com situações-problema resolvidas por meio de regra de três simples ou composta.
Publicado por: Raul Rodrigues de OliveiraQuestões
-
Questão 1
(Ifal) Um técnico em edificações percebe que necessita de 9 pedreiros para construir uma casa em 20 dias. Trabalhando com a mesma eficiência, quantos pedreiros são necessários para construir uma casa do mesmo tipo em 12 dias?
A) 6.
B) 12.
C) 15.
D) 18.
E) 21.
Alternativa C.
As grandezas são pedreiros e dias. Se aumentarmos a quantidade de pedreiros, o tempo será menor, logo essas grandezas são inversamente proporcionais. Montando a tabela, temos que:
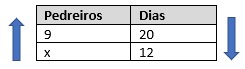
Como elas são inversamente proporcionais, multiplicamos reto
12x = 9 · 20
12x = 180
x = 180 : 12
x = 15
-
Questão 2
(Ifal) Uma editora utiliza 3 máquinas para produzir 1.800 livros num certo período. Quantas máquinas serão necessárias para produzir 5.400 livros no mesmo período?
A) 5.
B) 6.
C) 7.
D) 8.
E) 9.
Alternativa E.
As grandezas são: quantidade de máquinas e quantidade de livros. Sabemos que, quanto maior o número de máquinas, maior será a quantidade de livros impressos, logo essas grandezas são diretamente proporcionais. Montando a tabela, temos que:
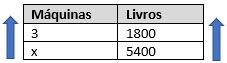
Como as grandezas são diretamente proporcionais, multiplicaremos cruzado:
1800x = 3 · 5400
1800x = 16200
x= 16200 : 1800
x = 9
-
Questão 3
(Cefet-MG) Em uma empresa, 10 funcionários produzem 150 peças em 30 dias úteis. O número de funcionários que a empresa vai precisar para produzir 200 peças, em 20 dias úteis, é igual a
A) 18.
B) 20.
C) 22.
D) 24.
Alternativa B.
As grandezas são: quantidade de funcionários, quantidade de peças e dias. Queremos encontrar o número de funcionários.
Fixando os dias, se eu aumentar a quantidade de funcionários, aumento a produção de peças, logo quantidade de funcionários e quantidade de peças são diretamente proporcionais.
Agora, fixando a quantidade de peças, se eu aumentar a quantidade de funcionários, o tempo necessário para produção será menor, logo essas grandezas são inversamente proporcionais.

Montando a equação e invertendo a razão do tempo, temos que:
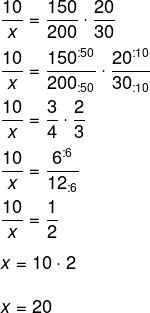
-
Questão 4
(Unifor) Quinze operários, trabalhando 8 horas por dia, demoram 16 dias para fazer um muro de 80 metros de comprimento. Se a quantidade de operários fosse reduzida para 10, a quantidade de horas, por dia, que precisariam trabalhar para, em 24 dias, fazerem um muro de 90 metros de comprimento, com a mesma espessura e altura que o anterior, é de:
A) 6.
B) 7.
C) 8.
D) 9.
E) 10.
Alternativa D.
Primeiro encontraremos a quantidade de horas trabalhadas na primeira situação. Multiplicando a quantidade de horas diárias pela quantidade de dias:
8 · 16 = 128 horas trabalhadas
Então, as grandezas são tempo, quantidade de operários e comprimento do muro.
Para analisar a proporcionalidade, vamos comparar as grandezas:
- Comparando o tempo com a quantidade de operários, se aumentarmos a quantidade de operários, o tempo necessário para construir o muro será menor, então as grandezas são inversamente proporcionais.
- Comparando o tempo com o comprimento do muro, se aumentarmos o comprimento do muro, o tempo necessário para construí-lo será maior, então as grandezas são diretamente proporcionais.
Construindo a tabela, temos que:

Montando a equação e invertendo a grandeza funcionários, temos que:
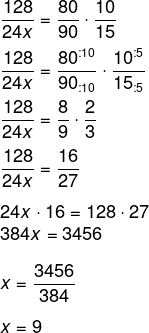
-
Questão 5
(Enem) Em um jogo on-line, cada jogador procura subir de nível e aumentar sua experiência, que são dois parâmetros importantes no jogo, dos quais dependem as forças de defesa e de ataque do participante. A força de defesa de cada jogador é diretamente proporcional ao seu nível e ao quadrado de sua experiência, enquanto sua força de ataque é diretamente proporcional à sua experiência e ao quadrado do seu nível. Nenhum jogador sabe o nível ou a experiência dos demais. Os jogadores iniciam o jogo no nível 1 com experiência 1 e possuem força de ataque 2 e de defesa 1. Nesse jogo, cada participante se movimenta em uma cidade em busca de tesouros para aumentar sua experiência. Quando dois deles se encontram, um deles pode desafiar o outro para um confronto, sendo o desafiante considerado o atacante. Compara-se então a força de ataque do desafiante com a força de defesa do desafiado e vence o confronto aquele cuja força for maior. O vencedor do desafio aumenta seu nível em uma unidade. Caso haja empate no confronto, ambos os jogadores aumentam seus níveis em uma unidade.
Durante um jogo, o jogador J1, de nível 4 e experiência 5, irá atacar o jogador J2, de nível 2 e experiência 6.
O jogador J1 venceu esse confronto porque a diferença entre sua força de ataque e a força de defesa de seu oponente era:
A) 112.
B) 88.
C) 60.
D) 28.
E) 24.
Alternativa B.
Calcularemos a força de defesa D e a força de ataque A.
D = kD · N · E²
A = kA · E · N²
Calculando o coeficiente de proporção de defesa, temos que:
1 = kD · 1·1
1 = kD
Agora calculando o coeficiente de proporção de ataque, temos que:
2 = kA · 1 · 1
2 = kA
Substituindo os valores do jogador J1, que possui nível 4 e experiência igual a 5:
N = 4 e E = 5
A = kA . E . N²
A = 2 · 5 · 4² = 160
Substituindo os valores dados para o J2:
N = 2 e E = 6
D = kD · N · E²
F = 1 · 2 · 6² = 72.
Então, a diferença entre o ataque e a defesa é:
160 - 72 = 88
-
Questão 6
(Enem) Em uma embalagem de farinha, encontra-se a receita de um bolo, sendo parte dela reproduzida a seguir:

Possuindo apenas a colher medida indicada na receita, uma dona de casa teve que fazer algumas conversões para poder medir com precisão a farinha. Considere que a farinha e o fermento possuem densidades iguais.
Cada xícara indicada na receita é equivalente a quantas colheres medidas?
A) 10
B) 20
C) 40
D) 80
E) 320
Alternativa B.
Para calcular a quantidade de gramas em uma xícara, basta dividir 640 : 4 = 160 g.
Para calcular a capacidade de uma colher de medida, basta dividir 16 : 2 = 8 g.
Então, uma xícara vai valer 160 g : 8 g = 20 colheres.
-
Questão 7
(Enem) O rótulo da embalagem de um cosmético informa que a dissolução de seu conteúdo, de acordo com suas especificações, rende 2,7 litros desse produto pronto para o uso. Uma pessoa será submetida a um tratamento estético em que deverá tomar um banho de imersão com esse produto numa banheira com capacidade de 0,3 m³. Para evitar o transbordamento, essa banheira será preenchida em 80% de sua capacidade.
Para esse banho, o número mínimo de embalagens desse cosmético é:
A) 9.
B) 12.
C) 89.
D) 112.
E)134.
Alternativa C.
Se a capacidade da banheira é de 0,3 m³, sabemos que 0,3 m³ correspondem a 300 L.
80% de 300 = 0,8 · 300 = 240 L
Como cada embalagem rende 2,7 litros, então temos que:
240 : 2,7 = 88,88…
Sendo assim, serão necessárias 89 embalagens.
-
Questão 8
(BNB – FGV). Em uma agência bancária, dois caixas atendem em média seis clientes em 10 minutos. Considere que, nessa agência, todos os caixas trabalham com a mesma eficiência e que a média citada sempre é mantida. Assim, o tempo médio necessário para que cinco caixas atendam 45 clientes é de:
A) 45 minutos.
B) 30 minutos.
C) 20 minutos.
D) 15 minutos.
E) 10 minutos.
Alternativa B.
As grandezas envolvidas são caixas, clientes e tempo. A grandeza que possui a incógnita é o tempo, então vamos compará-la com as demais.
- Tempo e clientes: se eu aumento o número de clientes, eu aumento o tempo para atender esses clientes. Fixando a quantidade de caixas, logo a grandeza quantidade de clientes e tempo são diretamente proporcionais.
- Tempo e caixas: se eu diminuir o tempo, a quantidade de caixas necessárias para atender a mesma quantidade de cliente será maior, logo tempo e caixas são grandezas inversamente proporcionais. Montado a tabela, teremos:

Invertendo a fração que representa a quantidade de caixas, temos que:
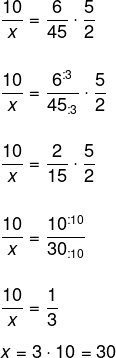
-
Questão 9
(Enem) Uma indústria tem um reservatório de água com capacidade para 900 m³. Quando há necessidade de limpeza do reservatório, toda a água precisa ser escoada. O escoamento da água é feito por seis ralos, e dura 6 horas quando o reservatório está cheio. Esta indústria construirá um novo reservatório, com capacidade de 500 m³, cujo escoamento da água deverá ser realizado em 4 horas, quando o reservatório estiver cheio. Os ralos utilizados no novo reservatório deverão ser idênticos aos do já existente.
A quantidade de ralos do novo reservatório deverá ser igual a:
A) 2.
B) 4.
C) 5.
D) 8.
E) 9.
Alternativa C.
Primeiro vamos identificar as três grandezas. São elas: capacidade, quantidade de ralos e tempo. A incógnita é a quantidade de ralos. Então, vamos analisar a proporção entre quantidades de ralos e as demais grandezas.
Ao comparar quantidade de ralos e tempo, fixando uma mesma capacidade para o reservatório, quanto maior a quantidade de ralos, menor será o tempo gasto, logo ralo e tempo são inversamente proporcionais.
Ao comparar quantidade de ralos e capacidade, fixando um mesmo tempo, se eu aumento a quantidade de ralos, posso aumentar a capacidade, então quantidade de ralos e capacidade são diretamente proporcionais. A tabelá ficará assim:

Invertendo a fração na grandeza tempo, temos que:
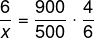
Vamos simplificar o máximo possível cada uma dessas frações:
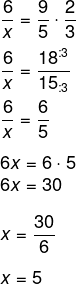
-
Questão 10
(Enem 2017) Uma indústria tem um setor totalmente automatizado. São quatro máquinas iguais, que trabalham simultânea e ininterruptamente durante uma jornada de 6 horas. Após esse período, as máquinas são desligadas por 30 minutos para manutenção. Se alguma máquina precisar de mais manutenção, ficará parada até a próxima manutenção.
Certo dia, era necessário que as quatro máquinas produzissem um total de 9 000 itens. O trabalho começou a ser feito às 8 horas. Durante uma jornada de 6 horas, produziram 6 000 itens, mas na manutenção observou-se que uma máquina precisava ficar parada. Quando o serviço foi finalizado, as três máquinas que continuaram operando passaram por uma nova manutenção, chamada manutenção de esgotamento.
Em que horário começou a manutenção de esgotamento?
A)16 h 45 min.
B) 18 h 30 min.
C) 19 h 50 min.
D) 21 h 15 min.
E) 22 h 30 min.
Alternativa B.
As grandezas são tempo, itens e quantidade de máquinas.
Comparando as grandezas, temos que:
- quanto maior o tempo, maior será a quantidade de itens produzidos, então tempo e itens são diretamente proporcionais;
- quanto maior o tempo, menor será a quantidade de máquinas necessárias, então tempo e máquinas são inversamente proporcionais.
Faltam 3000 itens, já que 6000 foram produzidos e a meta é 9000. Além disso, há 3 máquinas para atender a essa demanda. Montando a tabela, temos que:

Vamos inverter a razão das máquinas, então:
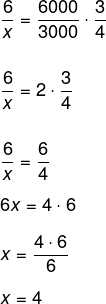
Somando os termos, se o trabalho iniciou-se às 8 horas (foram 6 horas com as 4 máquinas, mais 30 minutos de manutenção, mais as últimas 4 horas com as três máquinas), logo o trabalho vai se encerrar às 18 horas e 30 minutos.
-
Questão 11
(UFES) Dois sócios, Artur e Bruno, obtiveram como lucro de um negócio o valor de R$ 7.200,00. Esse lucro foi repartido em partes proporcionais ao que cada um havia investido. Artur investiu R$ 2.400,00 e Bruno investiu R$ 1.600,00 e, por isso, ao final, Artur teve direito a um lucro maior que Bruno. A diferença entre o lucro de Artur e o lucro de Bruno foi de:
A) R$ 1.200,00.
B)R$ 1.360,00.
C)R$ 1.400,00.
D)R$ 1.440,00.
E)R$ 1.500,00.
Alternativa D.
Somando os valores investidos por cada um:
1600 + 2400 = 4000
Foi investido um total R$ 4000 reais. Sabemos que 4000 está para 7200, assim como 2400 está para o lucro de Artur. Montando a tabela, temos que:
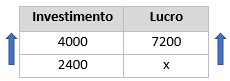
Quem investiu mais recebe mais, o que faz com que essas grandezas sejam diretamente proporcionais. Multiplicando cruzado, vamos encontrar o lucro do Artur:
4000x = 7200 · 2400
4000x = 17280000
x = 17280000/4000
x = 4320.
Se Artur lucrou 4320 reais, então Bruno teve um lucro de 7200 – 4320 = 2880. A diferença entre os lucros é de:
4320 – 2880 = 1440
-
Questão 12
(UNA Concursos) Um pintor gasta 2 galões de tinta para pintar uma parede de 45 m². Responda quantos litros de tinta serão necessários para pintar 135 m², sabendo que cada galão contém 3,6 L.
A) 23L
B) 19,3L
C) 28,8L
D) 21,6L
Alternativa D.
Se cada galão tem 3,6 L, então 2 galões têm 7,2 L. Sabemos que 7,2 L pintam 45 m², então as grandezas são volume de tinta e área a ser pintada. São grandezas diretamente proporcionais, pois, quanto maior a área, maior a quantidade de tinta necessária.
Montando a tabela:
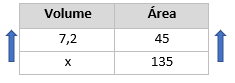
Multiplicando cruzado, temos que:
45x = 7,2 · 135
45x = 972
x= 972/45
x = 21,6
-
Questão 13
(Vunesp) Sabe-se que 15 funcionários conseguem arquivar 450 processos por dia. Vinte e cinco funcionários, com a mesma capacidade dos anteriores, arquivariam por dia uma quantidade de processos igual a:
A) 450.
B) 750.
C) 425.
D) 585.
E) 675.
Alternativa B.
As grandezas são funcionários e processos. Sabendo que, quanto maior a quantidade de funcionários, maior será a quantidade de processos arquivados, então as grandezas são diretamente proporcionais. Construiremos a tabela e multiplicaremos cruzado:

15x = 25 · 450
15 x = 11250
x = 11250 ÷ 15
x = 750
-
Questão 14
(Enem) Um dos grandes problemas enfrentados nas rodovias brasileiras é o excesso de carga transportada pelos caminhões. Dimensionado para o tráfego dentro dos limites legais de carga, o piso das estradas se deteriora com o peso excessivo dos caminhões. Além disso, o excesso de carga interfere na capacidade de frenagem e no funcionamento da suspensão do veículo, causas frequentes de acidentes.
Ciente dessa responsabilidade e com base na experiência adquirida com pesagens, um caminhoneiro sabe que seu caminhão pode carregar no máximo 1 500 telhas ou 1 200 tijolos.
Considerando esse caminhão carregado com 900 telhas, quantos tijolos, no máximo, podem ser acrescentados à carga de modo a não ultrapassar a carga máxima do caminhão?
a) 300 tijolos
b) 360 tijolos
c) 400 tijolos
d) 480 tijolos
e) 600 tijolos
Alternativas D.
As grandezas são tijolos e telhas.
Sabemos que no caminhão cabem 1500 telhas, mas foram colocadas 900 telhas, logo caberiam ainda mais 600 telhas. Porém, em vez de telhas, serão colocados tijolos que equivalem a essas 600 telhas restantes, então faremos uma regra de três. As grandezas são diretamente proporcionais, pois mais telhas equivalem sempre a mais tijolos, logo multiplicaremos cruzado:
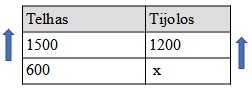
1500x = 600 · 1200
1500x = 720000
x = 720000 ÷ 1500
x = 480
-
Questão 15
(Vunesp) Uma torneira goteja sem parar, desperdiçando 2 litros de água a cada 44 minutos. Mantendo sempre esse mesmo gotejamento, o número aproximado de litros de água que serão desperdiçados em 4 horas será:
A) 11.
B) 10.
C) 9.
D) 8.
E) 7.
Alternativa A.
As grandezas são tempo e volume de água. Sabemos que, quanto maior o tempo, maior será o volume de água desperdiçado, então essas grandezas são diretamente proporcionais. Quando isso ocorre, multiplicamos cruzado. Além disso, 4 horas possuem 240 minutos, então:
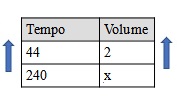
44x = 240 · 2
44x = 480
x= 480 ÷ 44
x= 11
-
Questão 16
(Enem) Uma mãe recorreu à bula para verificar a dosagem de um remédio que precisava dar a seu filho. Na bula, recomendava-se a seguinte dosagem: 5 gotas para cada 2 kg de massa corporal a cada 8 horas.
Se a mãe ministrou corretamente 30 gotas do remédio a seu filho a cada 8 horas, então a massa corporal dele é de:
A) 12 kg.
B) 16 kg.
C) 24 kg.
D) 36 kg.
E) 75 kg.
Alternativa A.
As grandezas são quantidade de gotas e a massa da criança. Sabemos que, quanto maior a massa, maior o número de gotas a serem ministradas para a criança, então temos grandezas diretamente proporcionais, logo:
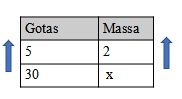
5x = 30 · 2
5x = 60
x = 60 ÷ 5
x = 12
-
Questão 17
(Enem 2015) Uma confecção possuía 36 funcionários, alcançando uma produtividade de 5 400 camisetas por dia, com uma jornada de trabalho diária dos funcionários de 6 horas. Entretanto, com o lançamento da nova coleção e de uma nova campanha de marketing, o número de encomendas cresceu de forma acentuada, aumentando a demanda diária para 21 600 camisetas. Buscando atender essa nova demanda, a empresa aumentou o quadro de funcionários para 96. Ainda assim, a carga horária de trabalho necessita ser ajustada. Compartilhe
Qual deve ser a nova jornada de trabalho diária dos funcionários para que a empresa consiga atender a demanda?
A) 1 hora e 30 minutos.
B) 2 horas e 15 minutos.
C) 9 horas.
D) 16 horas.
E) 24 horas.
Alternativa C.
Primeiro vamos identificar as grandezas, que são: quantidade de funcionários, quantidade de camisetas e horas trabalhadas. Como nós queremos calcular as horas trabalhadas, vamos comparar essa grandeza com as demais:
- Se o tempo de trabalho for maior, a quantidade de funcionários necessários será menor (inversamente proporcionais).
- Se o tempo de trabalho for maior, a quantidade de camisetas produzidas será maior (diretamente proporcionais).
Podemos montar a tabela que descreve a situação:
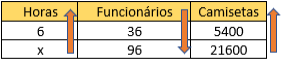
Agora montando a regra de três composta e escrevendo o inverso da fração de funcionários, temos que:

-
Questão 18
(Enem) Um pintor cobra R$ 240,00 por dia de trabalho, que equivale a 8 horas de trabalho num dia. Quando é chamado para um serviço, esse pintor trabalha 8 horas por dia com exceção, talvez, do seu último dia nesse serviço. Nesse último dia, caso trabalhe até 4 horas, ele cobra metade do valor de um dia de trabalho. Caso trabalhe mais de 4 horas, cobra o valor correspondente a um dia de trabalho. Esse pintor gasta 8 horas para pintar uma vez uma área de 40 m². Um cliente deseja pintar as paredes de sua casa, com uma área total de 260 m². Ele quer que essa área seja pintada o maior número possível de vezes para que a qualidade da pintura seja a melhor possível. O orçamento desse cliente para a pintura é de R$ 4 600,00.
Quantas vezes, no máximo, as paredes da casa poderão ser pintadas com o orçamento do cliente?
A) 1
B) 2
C) 3
D) 5
E) 6
Alternativa B.
Para pintar 260 m², a cada mão, sabemos que 260 : 40 = 6,5 dias. Como no último dia ele cobra metade do valor, então 6,5 · 240 = 1560,00 por vez que a parede for pintada.
Realizando a divisão, temos que 4600 : 1560 = 2,95. O número de vezes que essa parede pode ser pintada é, no máximo, 2.
-
Questão 19
(Enem 2009) Uma escola lançou uma campanha para seus alunos arrecadarem, durante 30 dias, alimentos não perecíveis para doar a uma comunidade carente da região. Vinte alunos aceitaram a tarefa e nos primeiros 10 dias trabalharam 3 horas diárias, arrecadando 12 kg de alimentos por dia. Animados com os resultados, 30 novos alunos somaram-se ao grupo, e passaram a trabalhar 4 horas por dia nos dias seguintes até o término da campanha.
Admitindo-se que o ritmo de coleta tenha se mantido constante, a quantidade de alimentos arrecadados ao final do prazo estipulado seria de:
A) 920 kg.
B) 800 kg.
C) 720 kg.
D) 600 kg.
E) 570 kg.
Alternativa A.
As grandezas são quantidade de alunos, tempo e peso. Sabendo que o peso é a nossa incógnita, vamos comparar as grandezas:
-
Peso e quantidade de alunos são grandezas diretamente proporcionais, pois, quanto maior a quantidade de alunos, maior será a quantidade de alimentos arrecadada.
-
Peso e dias são também grandezas diretamente proporcionais, pois, quanto maior a quantidade de dias, maior será a quantidade arrecadada.
Para facilitar, sabemos que eles trabalharam por 10 dias, 3 horas por dia, então trabalharam 30 horas.
Agora eles vão trabalhar durante 20 dias, 4 horas por dia, ou seja, 80 horas. Se a coleta foi de 12 kg por dia, ao final dos 10 dias foram coletados 120 kg. Como eram 20 alunos e foram acrescentados mais 30, então serão 50 alunos.
Montando a tabela, temos que:

Calculando a regra de três:
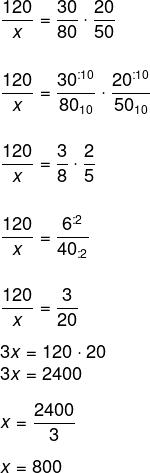
Como nos 10 primeiros dias foram arrecadados 120 kg e, nos outros 20, 800 kg, então o total foi de:
120 + 800 = 920
-
-
Questão 20
(Uneb) Três amigos abriram juntos uma loja de insumos agrícolas. O primeiro investiu R$ 5000,00; o segundo, R$ 7000,00 e o terceiro, R$ 8000,00. Depois de certo tempo, foi apurado um lucro de R$ 42000,00.
Nessas condições, pode-se afirmar que a diferença entre as partes do lucro a que os dois sócios que mais investiram capital para montar o negócio têm direito, em reais, é igual a:
A) 1800
B) 1900
C) 2000
D) 2100
E) 2200
Alternativa D.
O investimento inicial é igual à soma dos investimentos, ou seja, 7000 + 5000 + 8000 = 20000.
Sabemos que o lucro será proporcional ao valor investido. Calcularemos primeiro o lucro do amigo que investiu R$ 8.000,00:
Investimento
Lucro
20.000
420.000
8.000
x
20.000x = 420.000 · 8.000
20.000x = 3.360.000.000
x = 3.360.000.000 : 20.000
x = 168.000
Agora calcularemos o lucro do amigo que investiu R$ 7.000,00:
Investimento
Lucro
20.000
420.000
7.000
y
20.000x = 420.000 · 7.000
20.000x = 2.940.000.000
y = 2.940.000.000 : 20.000
y = 147.000
Calculando a diferença entre x e y, temos que 168.000 – 147.000 = 21.000.