Enem: lista de exercícios sobre transformações de unidades
(Enem 2016) A London Eye é uma enorme roda-gigante na capital inglesa. Por ser um dos monumentos construídos para celebrar a entrada do terceiro milênio, ela também é conhecida como Roda do Milênio. Um turista brasileiro, em visita à Inglaterra, perguntou a um londrino o diâmetro (destacado na imagem) da Roda do Milênio e ele respondeu que ele tem 443 pés.
Não habituado com a unidade pé, e querendo satisfazer sua curiosidade, esse turista consultou um manual de unidades de medidas e constatou que 1 pé equivale a 12 polegadas, e que 1 polegada equivale a 2,54 cm. Após alguns cálculos de conversão, o turista ficou surpreendido com o resultado obtido em metros.
Qual a medida que mais se aproxima do diâmetro da Roda do Milênio, em metro?
A) 53
B) 94
C) 113
D) 135
E) 145
Alternativa D.
Sabemos que 1 pé é igual a 12 polegadas e que cada polegada é igual a 2,54 cm, então a quantidade de centímetro em um pé é:
1 pé = 12 · 2,54 = 30,48 cm
Agora encontraremos o comprimento do diâmetro em centímetros.
443 ·30,48 = 13.502,64 cm
Para converter de cm para m, basta dividir por 100, então: 13.502,64 : 100 = 135,0264 m, que são aproximadamente 135 m.
Mário sabe que sua caixa d’água está com problemas. Para a realização do reparo, foi dito a ele que a caixa d’água deveria estar, no máximo, com 625 mil centímetros cúbicos de água, o que representa um volume máximo de:
A) 62,5 litros.
B) 6,25 litros.
C) 0,625 litros.
D) 625 litros.
E) 6.250 litros.
Alternativa D.
Sabemos que 1 cm³ equivale a 1 ml, logo a capacidade máxima em ml é de 625000 ml. Para transformar de ml para litros, basta dividir por 1000, então:
625000 : 1000 = 625 litros
(Enem 2019) A bula de um antibiótico infantil, fabricado na forma de xarope, recomenda que sejam ministrados, diariamente, no máximo 500 mg desse medicamento para cada quilograma de massa do paciente. Um pediatra prescreveu a dosagem máxima desse antibiótico para ser ministrada diariamente a uma criança de 20 kg pelo período de 5 dias. Esse medicamento pode ser comprado em frascos de 10 mL, 50 mL, 100 mL, 250 mL e 500 mL. Os pais dessa criança decidiram comprar a quantidade exata de medicamento que precisará ser ministrada no tratamento, evitando a sobra de medicamento. Considere que 1 g desse medicamento ocupe um volume de 1 cm³.
A capacidade do frasco, em mililitro, que esses pais deverão comprar é:
A) 10.
B) 50.
C) 100.
D) 250.
E) 500.
Alternativa B.
Atendendo as recomendações médicas, sabemos que serão ministrados 500 mg do medicamento a cada quilo. Para transformar 500 mg em g, basta dividir por 1000, ou seja, 0,5 g a cada kg.
Como o paciente possui 20 kg, então 0,5 · 20 = 10 gramas do medicamento por dia.
O período do tratamento é de 5 dias, logo, até o final, será ingerido um total de 10 · 5 = 50 g.
Sabemos que 1 g corresponde a 1 cm³ e, além disso, que 1 cm³ corresponde a 1 ml, então 50 g correspondem a um frasco de 50 ml.
(Enem 2019) O projeto de transposição do Rio São Francisco consiste na tentativa de solucionar um problema que há muito afeta as populações do semiárido brasileiro, a seca. O projeto prevê a retirada de 26,4 m³/s de água desse rio. Para tornar mais compreensível a informação do volume de água a ser retirado, deseja-se expressar essa quantidade em litro por minuto.
Disponível em: www.infoescola.com. Acesso em: 28 out. 2015.
Com base nas informações, qual expressão representa a quantidade de água retirada, em litro por minuto?
A)(26,4 : 1000) × 60
B)(26,4 : 10) × 60
C) 26,4 × 1×60
D) 26,4×10×60
E) 26,4×1000×60
Alternativa E.
Sabemos que o projeto prevê a retirada de 26,4 m³/s, valor igual a 26,4 metros cúbicos de água por segundo.
Sabemos que 1 m³ corresponde a 1000 litros, então:
26,4 × 1000 litros por segundo
Além disso, 1 minuto é composto por 60 segundos, então o total de água retirada em litros é representado por:
26,4 × 1000 × 60
(UECE) Uma torneira está gotejando de maneira regular e uniforme. Observa-se que a cada 12 minutos o gotejamento enche um recipiente com volume de 0,000 020 m³. Considerando um litro equivalente ao volume de 1 dm³, é correto afirmar que o volume, em litros, do gotejamento ao final de 30 minutos é:
A) 0,15.
B) 0,36.
C) 0,24.
D) 0,05.
Alternativa: D
Para transformar de m³ para dm³, que equivale a 1 litro, basta multiplicar o valor por 1000:
1000 · 0,000 020 = 0,020 litro a cada 12 minutos
Agora utilizaremos regra de três para encontrar o volume em litros do gotejamento após 30 minutos.
|
Volume |
Tempo |
|
0,020 |
12 minutos |
|
x |
30 minutos |
Multiplicando cruzado, temos que:
12x = 0,020 · 30
12x = 0,6
x = 0,6 : 12
x = 0,05
O volume em litros será de 0,05.
(Enem 2011) Um mecânico de uma equipe de corrida necessita que as seguintes medidas realizadas em um carro sejam obtidas em metros:
a) distância entre os eixos dianteiro e traseiro;
b) altura b entre o solo e o encosto do piloto.
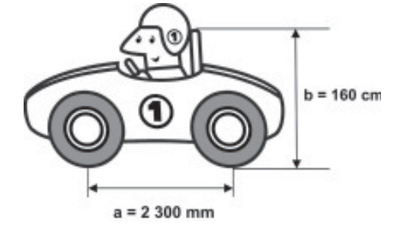
Ao optar pelas medidas a e b em metros, obtêm-se, respectivamente:
A) 0,23 e 0,16.
B) 2,3 e 1,6.
C) 23 e 16.
D) 230 e 160.
E) 2 300 e 1 600.
Alternativa B.
Realizando as conversões, para transformar 2300 mm para metros, basta dividir por 1000, então temos que:
2 300 : 1000 = 2,3 m
Para converter 160 cm em metros, dividimos por 100:
160 : 100 = 1,6 m
Então, a e b medem em metros, respectivamente, 2,3 e 1,6.
(Enem 2017) Em alguns países anglo-saxões, a unidade de volume utilizada para indicar o conteúdo de alguns recipientes é a onça fluida britânica. O volume de uma onça fluida britânica corresponde a 28,4130625 ml.
A título de simplificação, considere uma onça fluida britânica correspondendo a 28 ml.
Nessas condições, o volume de um recipiente com capacidade de 400 onças fluidas britânicas, em cm³, é igual a:
A) 11 200.
B) 1 120.
C) 112.
D) 11,2.
E) 1,12.
Alternativa A.
Sabemos que 28 ml correspondem a 1 onça fluida, então, para encontrar a quantidade de ml que possui 400 onças fluidas, basta calcular 400 · 28 = 11.200. Sabemos que 1 ml = 1 cm³. O volume do recipiente em cm³ é de 11.200.
(Enem 2013) Nos Estados Unidos a unidade de medida de volume mais utilizada em latas de refrigerante é a onça fluida (fl oz), que equivale a aproximadamente 2,95 centilitros (cL).
Sabe-se que o centilitro é a centésima parte do litro e que a lata de refrigerante usualmente comercializada no Brasil tem capacidade de 355 mL.
Assim, a medida do volume da lata de refrigerante de 355 mL, em onça fluida (fl oz), é mais próxima de:
A) 0,83
B) 1,20
C) 12,03
D) 104,73
E) 120,34
Alternativa C.
Primeiro convertemos cL para mL multiplicando por 10, então temos que 2,95 · 10 = 29,5 mL.
O volume da lata de refrigerante é de 355 mL. Para encontrar esse valor em fl oz, basta dividir por 29,5.
355 : 29,5 = 12,03
(Enem 2017) Em uma de suas viagens, um turista comprou uma lembrança de um dos monumentos que visitou. Na base do objeto há informações dizendo que se trata de uma peça em escala 1: 400, e que seu volume é de 25 cm³.
O volume do monumento original, em metro cúbico, é de:
A) 100
B) 400
C) 1600
D) 6250
E) 10000
Alternativa C.
Como linearmente a escala é de 1: 400, então o volume será de 1: 400³.
Como o volume da lembrancinha é de 25 cm³, então o volume real será de 25 · 400³.
25 · 400³ = 1 600 000 000 cm³
Mas queremos o volume do monumento em m³. Para realizar a conversão de cm³ para m³, dividimos por 1 000 000.
1 600 000 000 : 1 000 000 = 1 600 m³
(Enem Digital 2020) Três pessoas, X, Y e Z, compraram plantas ornamentais de uma mesma espécie que serão cultivadas em vasos de diferentes tamanhos. O vaso escolhido pela pessoa X tem capacidade de 4 dm³. O vaso da pessoa Y tem capacidade de 7 000 cm³ e o de Z tem capacidade igual a 20 L. Após um tempo do plantio das mudas, um botânico que acompanha o desenvolvimento delas realizou algumas medições e registrou que a planta que está no vaso da pessoa X tem 0,6 m de altura. Já as plantas que estão nos vasos de Y e Z têm, respectivamente, alturas medindo 120 cm e 900 mm.
O vaso de maior capacidade e a planta de maior altura são, respectivamente, os de:
A) Y e X.
B) Y e Z.
C) Z e X.
D) Z e Y.
E) Z e Z.
Alternativa D.
Sabemos que:
1L = 1dm³ = 1000 cm³
Então, analisando a capacidade, temos que:
X → 4 dm³ = 1L
Y → 7000 cm³ = 7L
Z → 20 L
Logo, o Z é o que possui maior capacidade.
Agora analisando a altura dos vasos, temos que:
1 m = 100 cm = 1000 mm
X → 0,6 m
Y → 120 cm → 1,2 m
Z → 900 mm → 0,9m
O maior é o Y.
Então, o que tem maior capacidade e o que tem maior altura são, respectivamente, Z e Y.
(Enem 2020 Digital) É comum as cooperativas venderem seus produtos a diversos estabelecimentos. Uma cooperativa láctea destinou 4 m³ de leite, do total produzido, para análise em um laboratório da região, separados igualmente em 4000 embalagens de mesma capacidade.
Qual o volume de leite, em mililitro, contido em cada embalagem?
A) 0,1
B) 1,0
C) 10,0
D) 100,0
E) 1 000,0
Alternativa E.
Para encontrar a quantidade de mL por embalagens, primeiro é necessário converter 4 m³ para mL.
Sabemos que:
1 m³ = 1000 L e que 1 L = 1 000 mL
Então, temos que 1 m³ → 1 000 000 mL.
Como foram produzidos 4 m³, convertendo para mL, há um total de 4 000 000 mL. Foi utilizado um total de 4000 embalagens. Realizando a divisão:
4 000 000 : 4 000 = 1 000 mL
(Enem 2019) O Sistema Métrico Decimal é o mais utilizado atualmente para medir comprimentos e distâncias. Em algumas atividades, porém, é possível observar a utilização de diferentes unidades de medida. Um exemplo disso pode ser observado no quadro.
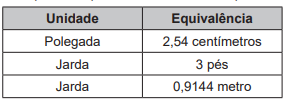
Assim, um pé, em polegada, equivale a:
A) 0,1200.
B) 0,3048.
C) 1,0800.
D) 12,0000.
E) 36,0000.
Alternativa D.
Sabemos que:
1 jarda → 3 pés
1 jarda → 0,9144 m
Então, temos que:
3 pés = 0,9144 m
1 pé = 0,9144 : 3 = 0,3048 m
Transformando 0,3048 m para cm, temos que 1 pé = 30,48 cm.
Agora analisando as polegadas, sabemos que:
1 polegada = 2,54 cm
Como 1 pé possui 30,48 cm, então realizando a divisão para saber quantas pelegadas possui um pé, temos que:
30,48 : 2,54 = 12 polegadas
(Enem 2016) Para que o pouso de um avião seja autorizado em um aeroporto, a aeronave deve satisfazer, necessariamente, as seguintes condições de segurança:
I. a envergadura da aeronave (maior distância entre as pontas das asas do avião) deve ser, no máximo, igual à medida da largura da pista;
II. o comprimento da aeronave deve ser inferior a 60 m;
III. a carga máxima (soma das massas da aeronave e sua carga) não pode exceder 110 t.
Suponha que a maior pista desse aeroporto tenha 0,045 km de largura, e que os modelos de aviões utilizados pelas empresas aéreas que utilizam esse aeroporto sejam dados pela tabela.
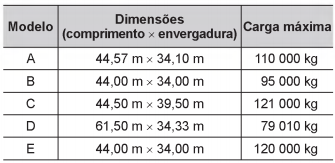
Os únicos aviões aptos a pousar nesse aeroporto, de acordo com as regras de segurança, são os de modelos:
A) A e C.
B) A e B.
C) B e D.
D) B e E.
E) C e E.
Alternativa B.
Sabemos que o comprimento da aeronave não deve ser superior a 60 m, o que faz com que o modelo D não seja uma possibilidade.
Sabemos também que, para transformar 110 toneladas em metros, basta multiplicar por 1000, logo a carga máxima dos aviões é de 110 000 kg. Note que os modelos C e E ultrapassam a carga máxima. Os modelos que não ultrapassam esse peso e nem o comprimento estabelecido são os modelos A e B.
(Omni) Márcio organizou um churrasco para seus amigos, e para que não faltasse uma grande quantidade de carne, Márcio compraria 300 gramas de carne por pessoa que confirmasse presença no churrasco. Com essas contas, Márcio comprou 19,2 kg de carne. No dia do churrasco, porém, 12 pessoas, que haviam confirmado presença, não puderam ir. Para não sobrar carne, quanta gramas, aproximadamente, de carne ficaria pra cada pessoa com essa nova divisão?
A) 243,75 g.
B) 288,88 g.
C) 300 g.
D) 369,23 g.
Alternativa D.
Como ele comprou 19,2 kg, para converter para gramas, basta multiplicar por 1000.
19,2 · 1000 = 19200 gramas
Como Márcio comprou 300 gramas por pessoa, então o total de pessoas que confirmaram é calculado pela divisão 19200 : 300 = 64 pessoas. Sabendo que 12 pessoas não compareceram, então havia 52 convidados.
Para calcular a quantidade de gramas por pessoas, basta realizar uma nova divisão:
19200 : 52 = 369,23 g
(Enem 2013) Uma torneira não foi fechada corretamente e ficou pingando, da meia-noite às seis horas da manhã, com a frequência de uma gota a cada três segundos. Sabe-se que cada gota d’agua tem volume de 0,2 mL.
Qual foi o valor mais aproximado do total de desperdiçada nesse período, em litros?
A) 0,2
B) 1,2
C) 1,4
D) 12,9
E) 64,8
Alternativa C.
O tempo de desperdício foi de 6 horas. Convertendo esse tempo para segundos, temos que 6 · 60 · 60 = 21600 segundos de desperdício.
Sabemos que, a 3 segundos cai uma gora, logo foi desperdiçado um total de 21600 : 3 = 7200 gotas.
Cada gota possui 0,2 mL, então foi um total de 7200 · 0,2 = 1440 mL de desperdício.
Transformando mL para litros, teremos 1440 : 1000 = 1,44 litros, que correspondem a aproximadamente 1,4 litro.
(Enem 2017) Uma empresa especializada em conservação de piscinas utiliza um produto para tratamento da água cujas especificações técnicas sugerem que seja adicionado 1,5 ml desse produto para cada 1000 l de água da piscina. Essa empresa foi contratada para cuidar de uma piscina de base retangular, de profundidade constante igual a 1,7 m, com largura e comprimento iguais a 3 m e 5 m, respectivamente. O nível da lâmina d’água dessa piscina é mantido a 50 cm da borda da piscina.
A quantidade desse produto, em mililitro, que deve ser adicionada a essa piscina de modo a atender às suas especificações técnicas é:
A) 11,25.
B) 27,00.
C) 28,80.
D) 32,25.
E) 49,50.
Alternativa B
Para calcular o volume da piscina, multiplicamos as suas três dimensões, ou seja:
3 · 5 · 1,7 = 18 m³
Para encontrar o volume em litros, basta multiplicar por 1000, ou seja, 18 · 1000 = 18000 l.
Sabemos que será aplicado 1,5 ml do produto para cada 1000 l, então temos que 18000 : 1000 = 18 porções do produto.
18 · 1,5 = 27 ml
(Enem 2014) Um show especial de Natal teve 45.000 ingressos vendidos. Esse evento ocorrerá em um estádio de futebol que disponibilizará 5 portões de entrada, com 4 catracas eletrônicas por portão. Em cada uma dessas catracas, passará uma única pessoa a cada 2 segundos. O público foi igualmente dividido pela quantidade de portões e catracas, indicados no ingresso para o show, para a efetiva entrada no estádio. Suponha que todos aqueles que compraram ingressos irão ao show e que todos passarão pelos portões e catracas eletrônicas indicados. Qual é o tempo mínimo para que todos passem pelas catracas?
A) 1 hora.
B) 1 hora e 15 minutos.
C) 5 horas.
D) 6 horas.
E) 6 horas e 15 minutos.
Alternativa B.
Existem 5 portões com 4 catracas cada, logo há 20 catracas. Foi vendido um total de 45000 ingressos. Supondo que passe a mesma quantidade de pessoas por catraca, então 45000 : 20 = 2250 pessoas por catraca. Como cada pessoa leva 2 segundos, então será gasto um total de 2250 · 2 = 4500 segundos.
Para converter 4500 segundos para horas, basta dividir por 360 4500 : 360 = 1,25 horas. Sabemos que 0,25 de uma hora corresponde a 1/4 de uma hora, logo: 15 minutos.
O tempo mínimo gasto é de 1 hora e 15 minutos.
(Enem 2015) Para economizar em suas contas mensais de água, uma família de 10 pessoas deseja construir um reservatório para armazenar a água captada das chuvas, que tenha capacidade suficiente para abastecer a família por 20 dias. Cada pessoa da família consome, diariamente, 0,08 m³ de água.
Para que os objetivos da família sejam atingidos, a capacidade mínima, em litros, do reservatório a ser construído deve ser:
A) 16.
B) 800.
C) 1 600.
D) 8 000.
E) 16 000.
Alternativa E.
Primeiro transformaremos o consumo de 0,08 m³ para litros multiplicando por mil:
0,08 · 1000 = 80 L por pessoa diariamente
Como são 10 pessoas, então o consumo diário da casa é calculado por 80 · 10 = 800 L.
O reservatório deve ter capacidade de 20 vezes o consumo diário, logo temos que:
800 · 20 = 16 000 litros
(Enem 2015) Atendendo à encomenda de um mecânico, um soldador terá de juntar duas barras de metais diferentes. A solda utilizada tem espessura de 18 milímetros, conforme ilustrado na figura.
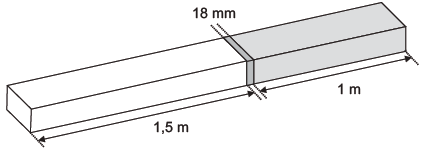
Qual o comprimento, em metros, da peça resultante após a soldagem?
A) 2,0230
B) 2,2300
C) 2,5018
D) 2,5180
E) 2,6800
Alternativa D.
Para encontrar o comprimento, em metros, vamos converter 18 mm para metros, dividindo por 1000:
18 : 1000 = 0,018
Analisando as alternativas, note que todas possuem 4 casas decimais, então, reescrevendo os números com 4 casas decimais e somando, temos que:
1,5000 + 0,0180 + 1, = 2,5180 metros
(Enem 2014) A maior piscina do mundo, registrada no livro Guiness, está localizada no Chile, em San Alfonso del Mar, cobrindo um terreno de 8 hectares de área.
Sabe-se que 1 hectare corresponde a 1 hectômetro quadrado.
Qual é o valor, em metros quadrados, da área coberta pelo terreno da piscina?
A) 8
B) 80
C) 800
D) 8 000
E) 80 000
Alternativa E
Sabemos que 1 hectare corresponde a 1 hm², então a piscina possui 8hm². Para converter para m², basta multiplicarmos por 10 000:
8 · 10 000 = 80 000 m² de área
