Enem: lista de exercícios sobre volume de sólidos geométricos
Com esta lista de exercícios, você testa seus conhecimentos sobre o cálculo de volume de sólidos geométricos e se prepara para a prova de Matemática do Enem
Publicado por: Raul Rodrigues de OliveiraQuestões
-
Questão 1
(Enem 2017) Para a Olimpíada de 2012, a piscina principal do Centro Aquático de Londres, medindo 50 metros de comprimento, foi remodelada para ajudar os atletas a melhorar suas marcas. Observe duas das melhorias:
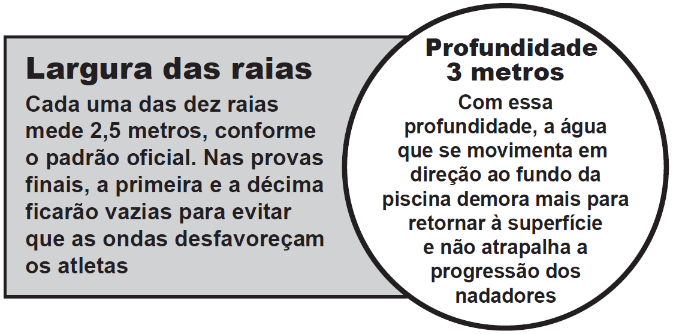
Veja, n. 2278, jul. 2012 (adaptado).
A capacidade da piscina em destaque, em metro cúbico, é igual a
A) 3750.
B) 1500.
C) 1250.
D) 375.
E) 150.
Alternativa A
Para calcular a largura, basta multiplicar o número de raias pelo comprimento, ou seja, 2,5 ⸳ 10 = 25 m.
Agora, multiplicaremos as três dimensões:
Capacidade = 25 ⸳ 3 ⸳ 50 = 3750 m³
-
Questão 2
(Enem 2016) Em regiões agrícolas, é comum a presença de silos para armazenamento e secagem da produção de grãos, no formato de um cilindro reto, sobreposto por um cone, e dimensões indicadas na figura. O silo fica cheio e o transporte dos grãos é feito em caminhões de carga cuja capacidade é de 20 m³. Uma região possui um silo cheio e apenas um caminhão para transportar os grãos para a usina de beneficiamento.
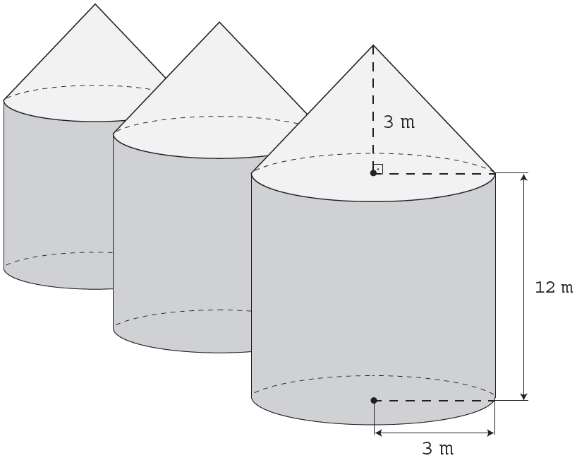
Utilize 3 como aproximação para π.
O número mínimo de viagens que o caminhão precisará fazer para transportar todo o volume de grãos armazenados no silo é
A) 6.
B) 16.
C) 17.
D) 18.
E) 21.
Alternativa D
Inicialmente, calcularemos o volume de um silo, que é composto por um cilindro e um cone.
Vcilindro = πr²h
Vcilindro = π ⸳ 3² ⸳ 12
Vcilindro = π ⸳ 9 ⸳ 12
Vcilindro = 108π
Agora, calcularemos o volume do cone.
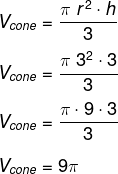
Utilizando π = 3 e somando o volume do cilindro ocm o do cone, temos que:
Vsilo = 9 ⸳ 3 + 108 ⸳ 3 = 351 m³
O caminhão leva 20 m³ por viagem, então o número de viagens necessárias é calculado pela divisão
35 : 20 = 17,55
Serão necessárias, portanto, 18 viagens.
-
Questão 3
(Enem 2016) Um petroleiro possui reservatório em formato de um paralelepípedo retangular com as dimensões dadas por 60 m x 10 m de base e 10 m de altura. Com o objetivo de minimizar o impacto ambiental de um eventual vazamento, esse reservatório é subdividido em três compartimentos, A, B e C, de mesmo volume, por duas placas de aço retangulares com dimensões de 7 m de altura e 10 m de base, de modo que os compartimentos são interligados, conforme a figura. Assim, caso haja rompimento no casco do reservatório, apenas uma parte de sua carga vazará.
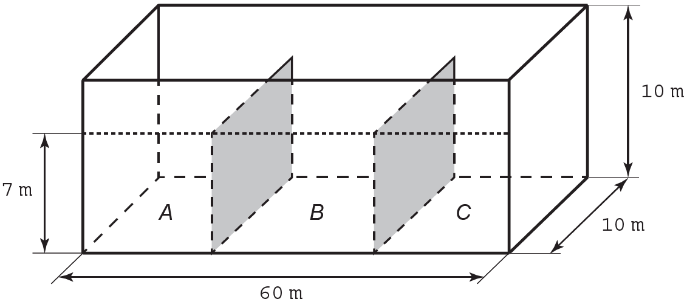
Suponha que ocorra um desastre quando o petroleiro se encontra com sua carga máxima: ele sofre um acidente que ocasiona um furo no fundo do compartimento C. Para fins de cálculo, considere desprezíveis as espessuras das placas divisórias.
Após o fim do vazamento, o volume de petróleo derramado terá sido de
A) 1,4 ⸳ 10³ m³.
B) 1,8 ⸳ 10³ m³.
C) 2,0 ⸳ 10³ m³.
D) 3,2 ⸳ 10³ m³.
E) 6,0 ⸳ 10³ m³.
Alternativa D
Para calcular o volume de um paralelepípedo retângulo, basta multiplicar as suas dimensões.
No vazamento será perdido o petróleo que está na parte superior, comum a A B e C, e também o que está no espaço C.
O volume do vazamento é dado por:
7 ⸳ 10 ⸳ 20 + 3 ⸳ 10 ⸳ 60 = 3200 m³ = 3,2 ⸳ 10³
-
Questão 4
(Enem 2018) Uma fábrica comercializa chocolates em uma caixa de madeira, como na figura.
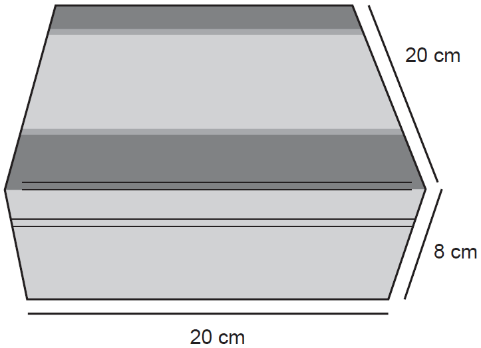
A caixa de madeira tem a forma de um paralelepípedo reto-retângulo cujas dimensões externas, em centímetro, estão indicadas na figura. Sabe-se também que a espessura da madeira, em todas as suas faces, é de 0,5 cm.
Qual é o volume de madeira utilizado, em centímetro cúbico, na construção de uma caixa de madeira como a descrita para embalar os chocolates?
a) 654.
b) 666.
c) 673.
d) 681.
e) 693.
Alternativa C
Calcularemos a diferença entre os volumes interno e externo da caixa, sabendo que no volume interno será retirado 1 cm de cada dimensão. Então, temos que:
V = 20 ⸳ 8 ⸳ 20 – 19 ⸳ 7 ⸳ 19 = 3200 – 2527 = 673 cm³
-
Questão 5
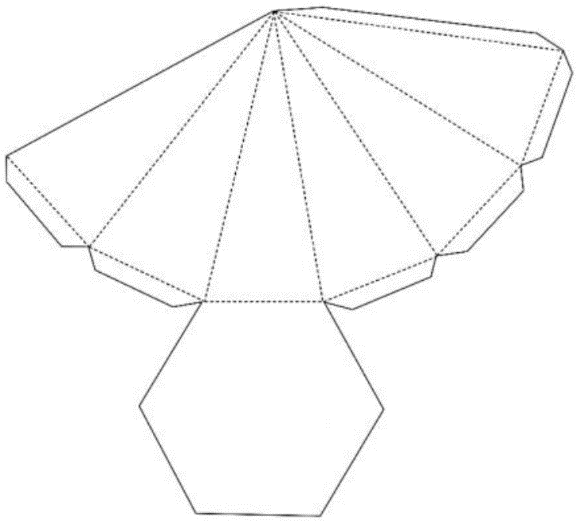
(UFPR 2018) A figura abaixo apresenta um molde para construção de uma pirâmide hexagonal regular. Para montar essa pirâmide, basta recortar o molde seguindo as linhas contínuas, dobrar corretamente nas linhas tracejadas e montar a pirâmide usando as abas trapezoidais para fixar sua estrutura com um pouco de cola. Sabendo que cada um dos triângulos tracejados nesse molde é isósceles, com lados medindo 5 cm e 13 cm, qual das alternativas abaixo mais se aproxima do volume dessa pirâmide?
A) 260 cm³.
B) 276 cm³.
C) 281 cm³.
D) 390 cm³.
E) 780 cm³.
Alternativa A
Para calcular o volume, precisamos da altura e da área da base. Calculando a altura, temos que:
5² + h² = 13²
25 + h² = 169
h² = 169 – 25
h² = 144
h = √144
h = 12
Agora, calcularemos a área da base, que é um hexágono de lado igual a 5.
Sabemos que:
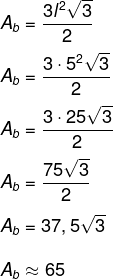
Então, calcularemos o volume da pirâmide pela fórmula:
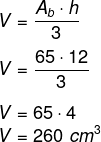
-
Questão 6
(UEG 2015) Suponha que haja laranjas no formato de uma esfera com 6 cm de diâmetro e que a quantidade de suco que se obtém ao espremer cada laranja é 2/3 de seu volume, sendo o volume dado em litros. Nessas condições, se quiser obter 1 litro de suco de laranja, deve-se espremer no mínimo (use π = 3,14).
A) 13 laranjas.
B) 14 laranjas.
C) 15 laranjas.
D) 16 laranjas.
Alternativa B
Sabemos que 1 litro = 1 dm³, então calcularemos o volume da laranja utilizando o raio em dm.
Diâmetro: 6 cm = 0,6 dm
Raio: 0,6 : 2 = 0,3 dm
Queremos calcular 2/3 do volume da laranja. Logo, temos que:
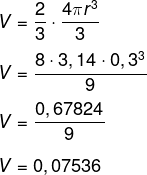
Sabemos que cada laranja produz 0,07536 litros. Então, para sabermos a quantidade de laranjas necessárias para produção de 1 litro, basta dividir: 1 : 0,07536 = 13,27 laranjas. Como não é possível haver 0,27 laranja, então arredondaremos o valor para 14 laranjas.
-
Questão 7
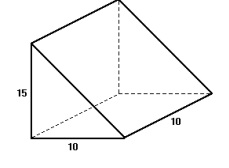
(FEI) De uma viga de madeira de seção quadrada de lado l = 10 cm extrai-se uma cunha de altura h = 15 cm, conforme a figura. O volume da cunha é:
A) 250 cm³.
B) 500 cm³.
C) 750 cm³.
D)1000 cm³.
E) 1250 cm³.
Alternativa C
Como a base é um triângulo, sabemos que:
Ab = (b · h) : 2
Ab = (10 · 15) : 2
Ab = 150 : 2
Ab = 75 cm²
Agora, calcularemos o volume:
V = Ab · h
V = 75 · 10
V = 750 cm³
-
Questão 8
(Enem 2018) Um artesão possui potes cilíndricos de tinta cujas medidas externas são 4 cm de diâmetro e 6 cm de altura. Ele pretende adquirir caixas organizadoras para armazenar seus potes de tinta, empilhados verticalmente com tampas voltadas para cima, de forma que as caixas possam ser fechadas. No mercado, existem cinco opções de caixas organizadoras, com tampa, em formato de paralelepípedo reto-retângulo, vendidas pelo mesmo preço, possuindo as seguintes dimensões internas:
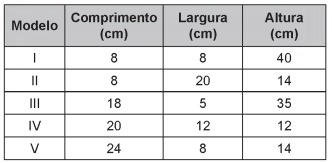
Qual desses modelos o artesão deve adquirir para conseguir armazenar o maior número de potes por caixa?
A) I.
B) II.
C) III.
D) IV.
E) V.
Alternativa D
Analisaremos a capacidade de cada um dos modelos:
-
Modelo I
-
Comprimento 8 cm → 8 : 4 = 2 latas
-
Largura 8 cm → 8 : 4 = 2 latas
-
Altura 40 cm → 40 : 6 = 6,66… isto é, 6 latas
-
Capacidade → 2 ⸳ 2 ⸳ 6 = 24 latas
-
-
Modelo II
-
Comprimento 8 cm → 8 : 4 = 2 latas
-
Largura 20 cm → 20 : 4 = 5 latas
-
Altura 14 cm → 14 : 6 = 2,333… isto é, 2 latas
-
Capacidade → 2 ⸳ 5 ⸳ 2 = 20 latas
-
-
Modelo III
-
Comprimento 18 cm → 18 : 4 = 4,5, isto é, 4 latas
-
Largura 5 cm → 5 : 4 = 1,25, isto é, 1 lata
-
Altura 35 cm → 35 : 6 = 5,8, isto é, 5 latas
-
Capacidade → 4 ⸳ 1 ⸳ 5 = 20 latas
-
-
Modelo IV
-
Comprimento 20 cm → 20 : 4 = 5 latas
-
Largura 12 cm → 12 : 4 = 3 latas
-
Altura 12 cm → 12 : 6 = 2 latas
-
Capacidade → 5 ⸳ 3 ⸳ 2 = 30 latas
-
-
Modelo V
-
Comprimento 24 cm → 24 : 4 = 6 latas
-
Largura 8 cm → 8 : 4 = 2 latas
-
Altura 14 cm → 14 : 6 = 2,333… isto é, 2 latas
-
Capacidade → 6 ⸳ 2 ⸳ 2 = 24 latas
-
A caixa organizadora que possui maior capacidade para as latas é o modelo IV.
-
-
Questão 9
(Enem 2012 – PPL) Um reservatório de uma cidade estava com 30 m³ de água no momento em que iniciou um vazamento estimado em 30 litros por minuto. Depois de 20 minutos, a partir do início do vazamento, uma equipe técnica chegou ao local e gastou exatamente 2 horas para consertar o sistema e parar o vazamento. O reservatório não foi reabastecido durante todo o período em que esteve com o vazamento.
Qual foi o volume de água que sobrou no reservatório, em m³, no momento em que parou o vazamento?
A) 3,6.
B) 4,2.
C) 25,8.
D) 26,4.
E) 27,6.
Alternativa C
Sabemos que 2 horas e 20 minutos equivalem a 140 minutos. Nesse tempo vazaram 140 ⸳ 30 = 4200 L.
Como o reservatório possui 30 m³, então ele tem a capacidade de 30000 litros. Logo, restará um total de 30000 – 4200 = 25800 L = 25,8 m³.
-
Questão 10
(FGV) O volume de uma esfera de raio r é dado por V = 4/3 π r³. Um reservatório com formato esférico tem um volume de 36 π metros cúbicos. Sejam A e B dois pontos da superfície esférica do reservatório e seja m a distância entre eles, o valor máximo de m em metros é
A) 5,5.
B) 5.
C) 6.
D) 4,5.
E) 4.
Alternativa C
A maior distância entre dois pontos de uma esfera é o diâmetro dessa esfera. Como conhecemos seu volume, então é possível calcular o seu raio:
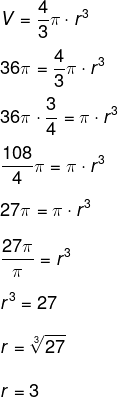
Como a maior distância possível é igual ao diâmetro, ou seja, ela mede o dobro do raio, então d = 6.
-
Questão 11
(Enem 2014) Uma pessoa comprou um aquário em forma de um paralelepípedo retângulo reto, com 40 cm de comprimento, 15 cm de largura e 20 cm de altura. Chegando em casa, colocou no aquário uma quantidade de água igual à metade de sua capacidade. A seguir, para enfeitá-lo, irá colocar pedrinhas coloridas, de volume igual a 50 cm³ cada, que ficarão totalmente submersas no aquário.
Após a colocação das pedrinhas, o nível da água deverá ficar a 6 cm do topo do aquário.
O número de pedrinhas a serem colocadas deve ser igual a
A) 48.
B) 72.
C) 84.
D) 120.
E) 168.
Alternativa A
Para encontrar o volume desejado, basta lembrar que o volume da pedrinha será igual ao volume que aumentou no líquido.
A metade da capacidade do aquário tem água e pedrinhas, e sabemos que a metade de 20 é 10. Calculando que 10 – 6 = 4 cm, logo, a altura da água aumentou 4 cm quando foram acrescentadas as pedrinhas. Então, basta calcular o volume com altura igual a 4 cm.
V = 40 ⸳ 15 ⸳ 4 = 2400 cm³
Como cada pedrinha possui 50 cm³ de volume, temos que:
2400 : 50 = 48 pedrinhas
-
Questão 12
(Enem 2009) Uma fábrica produz velas de parafina em forma de pirâmide quadrangular regular com 19 cm de altura e 6 cm de aresta da base. Essas velas são formadas por 4 blocos de mesma altura — 3 troncos de pirâmide de bases paralelas e 1 pirâmide na parte superior —, espaçados de 1 cm entre eles, sendo que a base superior de cada bloco é igual à base inferior do bloco sobreposto, com uma haste de ferro passando pelo centro de cada bloco, unindo-os, conforme a figura.
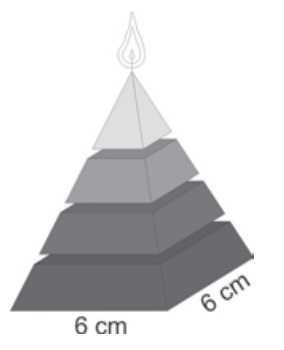
Se o dono da fábrica resolver diversificar o modelo, retirando a pirâmide da parte superior, que tem 1,5 cm de aresta na base, mas mantendo o mesmo molde, quanto ele passará a gastar com parafina para fabricar uma vela?
A) 156 cm³.
B) 189 cm³.
C) 192 cm³.
D) 216 cm³.
E) 540 cm³.
Alternativa B
Para encontrar o volume da nova pirâmide, vamos calcular a diferença entre o volume da pirâmide maior e o volume da pirâmide menor. Note que há 1 cm de distância entre os blocos, então a altura da pirâmide maior é 19 – 3 = 16 cm. A pirâmide maior tem 6 cm de lado da base. Como a base é um quadrado, então Ab = l² = 6² = 36.
Calculando o volume da pirâmide maior, temos que:
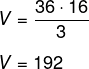
A altura da pirâmide menor na parte superior é 16 : 4 = 4 e da aresta é 6 : 4 = 1,5. Então, a área da base da pirâmide menor é 1,5² = 2,25. Calculando o volume, temos que:
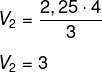
A diferença entre os volumes é de 192 – 3 = 189.
-
Questão 13
(Vunesp 2019) Analise o sólido geométrico da figura:
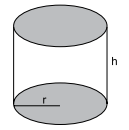
Se h = 48 cm e r = 17 cm, esse sólido tem volume igual a: (use π = 3,14)
A) 0,082 m³.
B) 0,068 m³.
C) 0,123 m³.
D) 0,044 m³.
E) 0,246 m³.
Alternativa D
O volume do cilindro é calculado pela fórmula V = πr²h
V = 3,14 · 17² · 48
V = 3,14 · 289 · 48
V = 3,14 · 289 · 48
V = 907,46 · 48
V = 43558,08 cm³
Note que as alternativas estão em m³. Para transformar de m³ para cm³, é necessário dividir por 1000000.
433558,08 : 1000000 = 0,043355809 m³
Utilizando o arredondamento, temos que o volume será igual a:
V = 0,044 m³
-
Questão 14
(Enem 2014 PPL) Uma fábrica de rapadura vende seus produtos empacotados em uma caixa com as seguintes dimensões: 25 cm de comprimento, 10 cm de altura e 15 cm de profundidade. O lote mínimo de rapaduras vendido pela fábrica é um agrupamento de 125 caixas dispostas conforme a figura.

Qual é o volume do lote mínimo comercializado pela fábrica de rapaduras?
A) 3750 cm³.
B) 18750 cm³.
C) 93750 cm³.
D) 468750 cm³.
E) 2343750 cm³.
Alternativa D
Encontraremos o volume de 125 caixas. Multiplicando as dimensões da caixa por 125, temos que:
125 V = 125 ⸳ 10 ⸳ 15 ⸳ 25 = 468750 cm³
-
Questão 15
(Enem 2010) Em um casamento, os donos da festa serviam champanhe aos seus convidados em taças com formato de um hemisfério (Figura 1), porém um acidente na cozinha culminou na quebra de grande parte desses recipientes. Para substituir as taças quebradas, utilizou-se um outro tipo com formato de cone (Figura 2). No entanto, os noivos solicitaram que o volume de champanhe nos dois tipos de taças fosse igual.
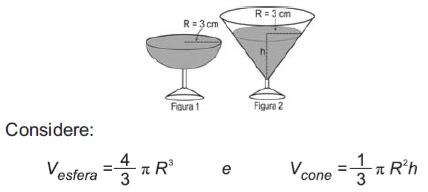
Sabendo que a taça com o formato de hemisfério é servida completamente cheia, a altura do volume de champanhe que deve ser colocado na outra taça, em centímetros, é de
A) 1,33.
B) 6,00.
C) 12,00.
D) 56,52.
E ) 113,04.
Alternativa B
Para que o volume seja o mesmo, basta igualar as equações. Note, porém, que a equação dada é a equação da esfera. Como há um hemisfério, basta dividirmos essa fórmula por 2. Como 2 ⸳ 3 = 6, temos que:
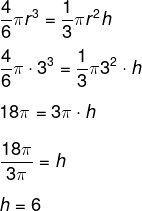
-
Questão 16
(Enem 2010) Dona Maria, diarista na casa da família Teixeira, precisa fazer café para servir as vinte pessoas que se encontram numa reunião na sala. Para fazer o café, Dona Maria dispõe de uma leiteira cilíndrica e copinhos plásticos, também cilíndricos.
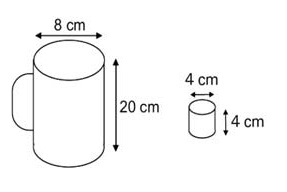
Com o objetivo de não desperdiçar café, a diarista deseja colocar a quantidade mínima de água na leiteira para encher os vinte copinhos pela metade.
Para que isso ocorra, Dona Maria deverá
A) encher a leiteira até a metade, pois ela tem um volume 20 vezes maior que o volume do copo.
B) encher a leiteira toda de água, pois ela tem um volume 20 vezes maior que o volume do copo.
C) encher a leiteira toda de água, pois ela tem um volume 10 vezes maior que o volume do copo.
D) encher duas leiteiras de água, pois cada uma tem um volume 10 vezes maior que o volume do copo.
E) encher cinco leiteiras de água, pois cada uma tem um volume 10 vezes maior que o volume do copo.
Alternativa A
Calcularemos os volumes da leiteira e do copo.
Vleiteira = πr²h = π ⸳ 4² ⸳ 20 = 320π
Vcopo = πr²h = π ⸳ 2² ⸳ 4 = 16πRealizando a divisão entre os volumes, temos que 320π : 16π = 20.
Como os copos serão preenchidos somente até a metade, preencher a leiteira até a metade será suficiente.
-
Questão 17
(Enem 2010) A siderúrgica “Metal Nobre” produz diversos objetos maciços utilizando o ferro. Um tipo especial de peça feita nessa companhia tem o formato de um paralelepípedo retangular, de acordo com as dimensões indicadas na figura que segue.
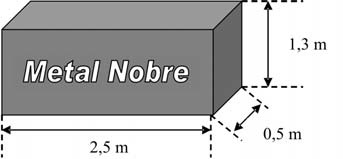
O produto das três dimensões indicadas na peça resultaria na medida da grandeza
A) massa.
B) volume.
C) superfície.
D) capacidade.
E) comprimento.
Alternativa B
Ao multiplicar as três dimensões, encontraremos o espaço ocupado por essa peça. Essa grandeza é conhecida como volume.
-
Questão 18
(Enem 2010) Um porta-lápis de madeira foi construído no formato cúbico, seguindo o modelo ilustrado a seguir. O cubo de dentro é vazio. A aresta do cubo maior mede 12 cm e a do cubo menor, que é interno, mede 8 cm.
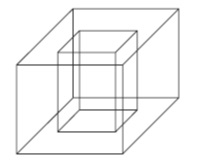
O volume de madeira utilizado na confecção desse objeto foi de:
A) 12 cm³.
B) 64 cm³.
C) 96 cm³.
D) 1216 cm³.
E) 1728 cm³.
Alternativa D
Para encontrar o volume do porta-lápis, basta calcular a diferença entre o volume do cubo maior e do cubo menor:
12³ – 8³ = 1728 – 512 = 1216 cm³
-
Questão 19
(Enem 2019 PPL) Para decorar sua casa, uma pessoa comprou um vaso de vidro em forma de um paralelepípedo retangular, cujas medidas internas são: 40 cm de comprimento, 35 cm de largura e 60 cm de altura. Em seguida, foi até uma floricultura e escolheu uma planta aquática para colocar nesse vaso. Segundo uma proposta do gerente do local, essa pessoa avaliou a possibilidade de enfeitar o vaso colocando uma certa quantidade de pedrinhas artificiais brancas, de volume igual a 100 cm3 cada uma delas, que ficarão totalmente imersas na água que será colocada no vaso. O gerente alertou que seria adequado, em função da planta escolhida, que metade do volume do vaso fosse preenchido com água e que, após as pedrinhas colocadas, a altura da água deveria ficar a 10 cm do topo do vaso, dando um razoável espaço para o crescimento da planta. A pessoa aceitou as sugestões apresentadas, adquirindo, além da planta, uma quantidade mínima de pedrinhas, satisfazendo as indicações do gerente.
Nas condições apresentadas, a quantidade de pedrinhas compradas foi
A) 140.
B) 280.
C) 350.
D) 420.
E) 700.
Alternativa B
Inicialmente, calcularemos o volume total do aquário.
V = 40 ⸳ 35 ⸳ 60 = 84000 cm³
Como ele está cheio até a metade, dividindo por 2 teremos 42000 cm³.
Agora, o volume com a altura de 50 cm:
V = 40 ⸳ 35 ⸳ 50 = 70000 cm³
A diferença entre eles é de:
70000 – 42000 = 28000 cm³
Finalmente, basta dividir o volume encontrado pelo volume das pedrinhas:
28000 : 100 = 280 pedrinhas
-
Questão 20
(Udesc 2015) Uma bola esférica é composta por 24 faixas iguais, como indica a figura.
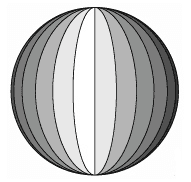
Sabendo-se que o volume da bola é de 2304π cm³, então a área da superfície de cada faixa é de:
A) 20π cm².
B) 24π cm².
C) 28π cm².
D) 27π cm².
E) 25π cm².
Alternativa B
Primeiramente, encontraremos o raio da esfera. Conhecendo seu volume, vamos calcular seu raio.
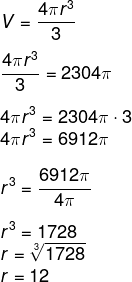
Agora, calcularemos a área total, sabendo que o raio mede 12 cm.

Para encontrar a área de cada faixa, basta dividir a área total por 24.
576π : 24 = 24π cm²