Exercícios sobre ângulos

Sobre a classificação dos ângulos, marque a alternativa correta:

A) Um ângulo é classificado como reto quando ele possui medida menor ou igual a 90º.

B) Dois ângulos são complementares quando a soma deles é igual a 180º.

C) Um ângulo é classificado como agudo quando a sua medida é menor do que 90º.

D) Dois ângulos cuja soma é igual a 90º graus são conhecidos como ângulos obtusos.

Sabendo que a soma dos ângulos internos de um quadrilátero é sempre igual a 360º, em um quadrilátero em específico, a medida dos seus ângulos internos é proporcional aos números 3, 5, 6, 10. O valor do menor ângulo é:

A) 15º

B) 25º

C) 45º

D) 60º

E) 75º

Sabendo que o ângulo EÂG é reto, o valor do ângulo x é:

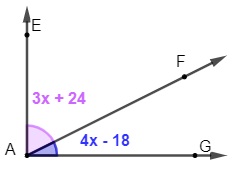
A) 12º

B) 30º

C) 42º

D) 45º

E) 60º

Sabendo que os ângulos são suplementares, e analisando a imagem a seguir, o valor de x é igual a:

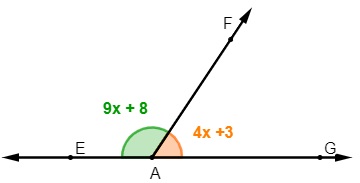
A) 10º

B) 11º

C) 12º

D) 13º

E) 14º

Durante a elaboração de um projeto, um arquiteto coletou algumas medidas de ângulos na planta. As medições foram 90º, 120º e 75º. Na geometria sabemos que os ângulos podem ser classificados de acordo com a sua medida. Nesse caso, os ângulos coletados pelo arquiteto são, respectivamente:

A) agudo, reto, obtuso

B) agudo, obtuso, reto

C) reto, agudo, obtuso

D) reto, obtuso, agudo

E) obtuso, obtuso, agudo

(Enem 2018) A rosa dos ventos é uma figura que representa oito sentidos, que dividem o círculo em partes iguais.

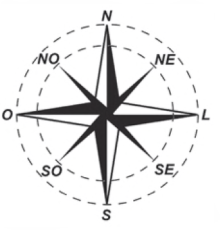
Uma câmera de vigilância está fixada no teto de um shopping e sua lente pode ser direcionada remotamente, através de um controlador, para qualquer sentido. A lente da câmera está apontada inicialmente no sentido oeste e o seu controlador efetua três mudanças consecutivas, a saber:

• 1ª mudança: 135° no sentido anti-horário;

• 2ª mudança: 60° no sentido horário;

• 3ª mudança: 45° no sentido anti-horário.

Após a 3ª mudança, ele é orientado a reposicionar a câmera, com a menor amplitude possível, no sentido noroeste (NO) devido a um movimento suspeito de um cliente.

Qual mudança de sentido o controlador deve efetuar para reposicionar a câmera?

A) 75º no sentido horário

B) 105º no sentido anti-horário

C) 120º no sentido anti-horário

D) 135º no sentido anti-horário

E) 165º no sentido horário

(Enem 2017) A imagem apresentada na figura é uma cópia em preto e branco da tela quadrada intitulada O peixe, de Marcos Pinto, que foi colocada em uma parede para exposição e fixada nos pontos A e B.

Por um problema na fixação de um dos pontos, a tela se desprendeu, girando rente à parede. Após o giro, ela ficou posicionada como ilustrado na figura, formando um ângulo de 45° com a linha do horizonte.

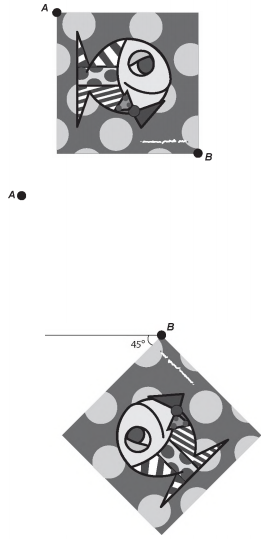
Para recolocar a tela na sua posição original, deve-se girá-la, rente à parede, no menor ângulo possível inferior a 360°. A forma de recolocar a tela na posição original, obedecendo ao que foi estabelecido, é girando-a em um ângulo de

A) 90º no sentido horário.

B) 135º no sentido horário.

C) 180º no sentido anti-horário.

D) 270º no sentido anti-horário.

E) 315º no sentido horário.

(IFG) Supondo que a'//a e b'//b, marque a alternativa correta.

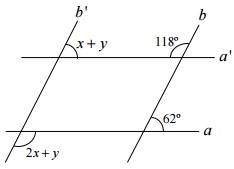
A) x = 31° e y = 31°

B) x = 56° e y = 6°

C) x = 6° e y = 32°

D) x = 28° e y = 34°

E) x = 34° e y = 28°

Analisando a imagem, podemos afirmar que a medida do menor ângulo é:

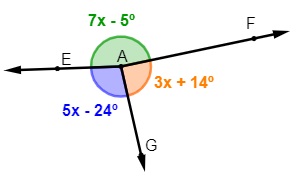
A) 95º

B) 89º

C) 77º

D) 64º

E) 25º

O ângulo α é complementar ao ângulo ꞵ e suplementar a um ângulo de 125º, então, a medida do ângulo ꞵ é:

A) 55º

B) 45º

C) 35º

D) 30º

E) 25º

Analisando a imagem seguinte, podemos afirmar que o valor de x + y é:

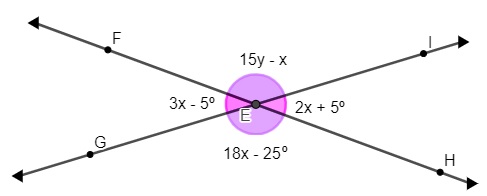
A) 15º

B) 11º

C) 10º

D) 21º

E) 24º

Sabendo que o seguimento AD é bissetriz do ângulo BÂC, então, o valor desse ângulo BÂC é:

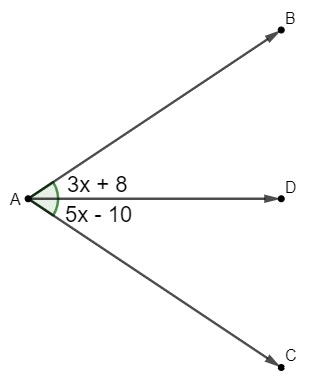
A) 25º

B) 35º

C) 50º

D) 70º

E) 75º