Home
Exercícios de Matemática
Exercícios sobre área do cilindro

Exercícios sobre área do cilindro

Esta lista de exercícios sobre área do cilindro te auxiliará na compreensão do cálculo da área de um dos sólidos geométricos mais presentes no nosso cotidiano. Publicado por: Raul Rodrigues de Oliveira

Imprimir

Questão 1

Um cilindro possui raio medindo 5 cm e altura igual a 8 cm, então sua área total é de:

(Use π = 3.)

A) 390 cm²

B) 350 cm²

C) 310 cm²

D) 280 cm²

E) 250 cm²

Ver resposta

Resposta

Alternativa A

Calcularemos a área total do cilindro:

$A_T=2\pi r\left(r+h\right)$

$A_T=2\cdot3\cdot5\left(5+8\right)$

$A_T=30\cdot13$

$A_T=390\ cm^2$

Questão 2

Um recipiente possui formato de cilindro com área igual a 720 π cm². Se o raio desse cilindro é de 12 cm, então sua altura é de:

A) 16 cm

B) 18 cm

C) 20 cm

D) 22 cm

E) 24 cm

Ver resposta

Resposta

Alternativa B

Se a área desse recipiente no formato de cilindro é 720 π cm², temos que:

$A_T=2\pi r\left(r+h\right)$

$720\pi=2\cdot\pi\cdot12\left(12+h\right)$

$720\pi=24\pi\left(12+h\right)$

$\frac{720\pi}{24\pi}=12+h$

$30=12+h$

$30-12=h$

$18=h$

$h=18\ cm$

Questão 3

Uma caixa d’água terá a sua área lateral pintada, e para realizar a pintura é necessário calcular essa área. Seu diâmetro é de 1,20 metro e sua altura é de 1,40 metro, então a área lateral dessa caixa é de:

A) 1,50 π m²

B) 1,56 π m²

C) 1,68 π m²

D) 1,72 π m²

E) 1,83 π m²

Ver resposta

Resposta

Alternativa C

A área lateral de um cilindro é dada pela fórmula:

$A_l=2\pi rh$

Se o diâmetro é de 1,2 metro, logo o raio é a metade, ou seja, r = 0,6 metro. Além disso, sabemos que a altura h = 1,40 metro:

$A_l=2\cdot\pi\cdot0,6\cdot1,40$

$A_l=1,68\pi{\ m}^2$

Questão 4

Um porta-joias possui formato cilíndrico, com área total igual a 244,92 cm². Se a altura desse porta-joias é de 10 cm, o raio dessa embalagem é de:

(Use π = 3,14.)

A) 2 cm

B) 3 cm

C) 4 cm

D) 5 cm

E) 6 cm

Ver resposta

Resposta

Alternativa B

Sabemos que:

$2\pi r\left(r+h\right)=244,92$

$2\cdot3,14r\left(r+10\right)=244,92$

$6,28r\left(r+10\right)=244,92$

$r\left(r+10\right)=\frac{244,92}{6,28}$

$r\left(r+10\right)=39$

$r^2+10r=39$

$r^2+10r-39=0$

Encontramos uma equação do 2º grau. Calculando as raízes dessa equação, temos que: a = 1, b = 10 e c = -39:

$\Delta=b^2-4ac$

$\Delta={10}^2-4\cdot1\cdot\left(-39\right)$

$\Delta=100+156$

$\Delta=256$

Agora, utilizando a fórmula de Bháskara:

$r=\frac{-b\pm\sqrt\Delta}{2a}$

$r=\frac{-10\pm\sqrt{256}}{2\cdot1}$

$r=\frac{-10\pm16}{2}$

$r_1=\frac{-10+16}{2}=\frac{6}{2}=3$

Note que $x_2$ é negativo, portanto, isso não faz sentindo, já que não existe raio negativo. Então, temos que r = 3 metros.

Questão 5

Qual é a medida do raio de um cilindro que possui área lateral igual a 104 π cm² e a altura igual a 8 cm?

A) 5,0 cm

B) 5,5 cm

C) 6,0 cm

D) 6,5 cm

E) 7,0 cm

Ver resposta

Resposta

Alternativa D

Sabemos que h = 8 e que $A_l=104\pi$ , então temos que:

$A_l=2\pi rh$

$104\pi=2\cdot\pi\cdot r\cdot8\$

$104\pi=16\pi r$

$\frac{104\pi}{16\pi}=r$

$6,5=r$

Então, temos que r = 6,5 cm.

Questão 6

Para melhor conservação dos galões de óleo de uma empresa, no formato cilíndrico, o dono decidiu passar tinta na base superior do galão e na área lateral. Sabendo que a altura de cada galão é de 1 metro e que o diâmetro é de 80 cm, então a área que será pintada mede, em centímetros quadrados: (Use π = 3.)

A) 3,5 mil

B) 3,9 mil

C) 13 mil

D) 35 mil

E) 39 mil

Ver resposta

Resposta

Alternativa E

Se o diâmetro é de 1 metro, então o raio é de 0,5 metro ou 50 centímetros. Calculando a área total, temos que:

$A_T=2\pi r\left(r+h\right)$

$A_T=2\cdot3\cdot50\left(50+80\right)$

$A_T=6\cdot50\cdot130$

$A_T=39000\ cm^2$

Questão 7

A área da base de um cilindro é de 36π cm². Se a altura desse cilindro é de 5 cm, sua área total, em cm², é de:

A) 168 π

B) 165 π

C) 156 π

D) 150 π

E) 147 π

Ver resposta

Resposta

Alternativa A

Se a área da base de um cilindro é $\pi r^2$ , temos que:

$36\pi=\pi r^2$

$36=r^2$

$r^2=36$

$r=\sqrt{36}$

$r=6$

Sabendo que o raio é 6, podemos calcular a área total do cilindro:

$A_T=2\pi r\left(r+h\right)$

$A_T=2\pi\cdot6\left(6+8\right)$

$A_T=12\pi\cdot14$

$A_T=168\pi$

Questão 8

A medida, em m², da área da superfície total de um cilindro circular reto tal que a medida da altura é de 3 metros e a medida do raio é de 2 metros é:

A) 15 π

B) 20 π

C) 25 π

D) 30 π

E) 35 π

Ver resposta

Resposta

Alternativa B

Calculando a área total:

$A_T=2\pi r\left(r+h\right)$

$A_T=2\cdot\pi\cdot2\left(2+3\right)$

$A_T=4\pi\cdot5$

$A_T=20\pi$

Questão 9

(Idecan) Um oficial de manutenção de equipamentos deseja pintar as áreas externas das bases inferiores de dois cilindros, A e B, cujas circunferências são 8 π cm e 10 π cm, respectivamente. Logo, ele necessitará de tinta suficiente para pintar uma área total igual a, em cm²:

A) 36 π

B) 41 π

C) 56 π

D) 82 π

Ver resposta

Resposta

Alternativa B

Para calcular a área total de cada um dos cilindros, primeiramente calcularemos os seus raios, utilizando a informação que temos sobre o comprimento da suas circunferências:

$C_A=8\pi$

$2\pi r_A=8\pi$

$r_A=\frac{8\pi}{2\pi}$

$r_A=4$

Então, o raio do cilindro A é 4 cm. Agora, o raio do cilindro B:

$C_B=10\pi$

$2\pi r_B=10\pi$

$r_B=\frac{10\pi}{2\pi}$

$r_B=5$

O raio do cilindro B é de 5 cm.

Calculando a soma da área total de cada um dos cilindros:

$A_P=A_{BA}+A_{BB}$

$A_P=\pi r_A^2+\pi r_B^2$

$A_P=\pi4^2+\pi5^2$

$A_P=16\pi+25\pi$

$A_P=41\pi$

Questão 10

(Cesgranrio — Petrobras) Uma fita retangular de 2 cm de largura foi colocada em torno de uma pequena lata cilíndrica de 12 cm de altura e 192 π cm³ de volume, dando uma volta completa em torno da lata, como ilustra o modelo abaixo.

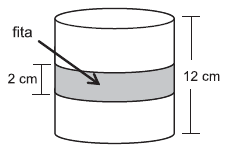
Ilustração de uma lata cilíndrica de 12 cm envolta por uma fita retangular de 2 cm.

A área da região da superfície da lata ocupada pela fita é, em cm², igual a

A) 8 π

B) 12 π

C) 16 π

D) 24 π

E) 32 π

Ver resposta

Resposta

Alternativa C

Queremos calcular a área lateral de um cilindro com 2 cm de altura, cujo raio é igual ao raio do cilindro maior. Como não sabemos o raio, utilizaremos as informações dadas para calculá-lo:

$V=\ 192\pi$

$\pi r^2h=192\pi$

$r^2\cdot12=192$

$r^2=\frac{192}{12}$

$r^2=16$

$r=\sqrt{16}$

$r=4$

Agora, calcularemos a área lateral:

$A_l=2\pi rh$

$A_l=2\pi\cdot4\cdot2$

$A_l=16\pi$

Temos que a = 1, b = 12 e c = - 96:

$\Delta=b^2-4ac$

$\Delta={12}^2-4\cdot1\cdot\left(-96\right)$

$\Delta=144+384$

$\Delta=528$

Agora, calculando Bháskara:

$r=\frac{-b\pm\sqrt\Delta}{2a}$

$r=\frac{-10\pm\sqrt{256}}{2\cdot\ 1}$

$r=\frac{-10\pm16}{2}$

$r_1=\frac{-10+16}{2}=\frac{6}{2}=3$

Questão 11

(Uece) Um cilindro circular reto de altura 7 cm tem volume igual a 28 π cm³. A área total desse cilindro, em cm², é de:

A) 30 π

B) 32 π

C) 34 π

D) 36 π

Ver resposta

Resposta

Alternativa D

Para calcular a área total desse cilindro, é necessário encontrar o valor do raio. Para isso, utilizaremos a fórmula do volume. O volume do cilindro é o produto entre a área da base e a altura:

$V=A_b\cdot h$

$28\pi=A_b\cdot7$

$\frac{28\pi}{7}=A_b\$

$A_b=4\pi$

A área da base do cilindro é $\pi r^2$ :

$\pi r^2=4\pi$

$r^2=4$

$r=\sqrt4$

$r=2$

Como já conhecemos a área da base, falta calcular a área lateral do cilindro:

$A_l=2\pi rh$

$A_l=2\pi\cdot2\cdot7$

$A_l=28\pi$

A área total será:

$A_T=2A_b+Al$

$A_T=2\cdot4\pi+28\pi$

$A_T=8\pi+28\pi$

$A_T=36\pi\ cm^2$

Questão 12

Em um condomínio, o reservatório de água tem forma de cilindro cuja base é um círculo de raio de 8 metros e 5 metros de altura. Para melhor conservação desse reservatório, a assembleia decidiu pintar a parte superior do reservatório e a sua área lateral. O pintor contratado cobrou um valor de R$ 7,00 para o metro quadrado pintado. Ao término do serviço, o valor devido ao pintor foi de: (Use π = 3.)

A) R$ 2328,00

B) R$ 2550,00

C) R$ 2870,00

D) R$ 2904,00

E) R$ 3024,00

Ver resposta

Resposta

Alternativa E

Primeiramente, calcularemos a área a ser pintada, que é a área lateral do cilindro mais a área de uma base:

$A_p=Al+A_b$

$A_p=2\pi rh+\pi r^2$

$A_p=2\cdot3\cdot5\cdot8+3\cdot8^2$