Exercícios sobre área do quadrado
Resolva esta lista de exercícios sobre área do quadrado e teste seus conhecimentos sobre o cálculo da área dessa figura plana.
Publicado por: Raul Rodrigues de OliveiraQuestões
-
Questão 1
Qual é a área de um quadrado cujo lado mede 12 cm?
Alternativa B
A área do quadrado é igual à medida do seu lado ao quadrado, então temos que:
\(A=l^2\)
\(A=12^2\)
\(A=144\ cm^2\)
-
Questão 2
Um terreno, que possui formato de um quadrado, tem o perímetro de 20 metros. A área desse terreno é de:
Alternativa B
O perímetro do quadrado é a soma dos seus 4 lados, então, para encontrar a medida de cada lado, basta dividir o perímetro por 4.
20 : 4 = 5
A área do quadrado é igual ao lado ao quadrado, como o lado mede 5 metros, temos que:
\(A=l^2\)
\(A=5^2\)
\(A=25\)
-
Questão 3
Na casa de Marcelo, há um quintal no formato quadrado com lados medindo 6 metros. Nesse quintal será colocado um tablado de formato também quadrado, com 2 metros de lado. O restante do quintal será todo cimentado. A área que será cimentada nesse terreno mede:
Alternativa C
Primeiro calcularemos a área do quintal:
\(A_{quinta}=6^2=36\)
Agora calcularemos a área do tablado:
\(A_{tablado}=2^2=4\)
A área a ser cimentada é a diferença entre a área do quintal e a área do tablado.
\(A=36-4=32\)
-
Questão 4
A diagonal de um terreno é de 8,4 metros. Sabendo que esse terreno possui formato de um quadrado, a medida da área desse terreno é igual a:
(Utilize \(\sqrt2\) = 1,4)
Alternativa B
A diagonal de um quadrado é igual a \(l \sqrt2\), então temos que:
\(l \sqrt2=8,4\)
Utilizando \(\sqrt2=1,4\)
\(l⋅1,4=8,4\)
\(l=\frac{8,4}{1,4}\)
\(l=6\)
A área desse terreno será de:
\(A=l^2\)
\(A=6^2\)
\(A=36\ m^2\)
-
Questão 5
Kárita possui um terreno com 256 m² de área, no formato de um quadrado. A medida do perímetro desse terreno é igual a:
Alternativa D
Para encontrar a medida do perímetro, primeiro calcularemos a medida do lado. Sabendo que a área é igual ao quadrado do lado, temos que:
\(l^2=256\)
\(l=\sqrt{256}\)
\(l=16\)
Se o lado mede 16 metros, então temos que:
\(P=4l\)
\(P=4⋅16\)
\(P=64\ m\)
-
Questão 6
Natália e Lara ganharam de presente da tia delas dois terrenos na cidade de Pirenópolis, no estado de Goiás. Esses terrenos possuem mesma área, entretanto, um deles é retangular e o outro é quadrado. As dimensões do terreno retangular é 24 metros de largura e 54 metros de comprimento, então a medida do lado do terreno quadrado é igual a:
Alternativa A
As áreas dos terrenos são iguais, então, calculando a área do terreno retangular, temos que:
\(A=24⋅54=1296\)
Como a área do terreno quadrado é igual ao lado ao quadrado, então temos que:
\(l^2=1296\)
\(l=\sqrt{1296}\)
\(l=36\)
-
Questão 7
Uma fábrica confecciona peças de ferro no formato de um quadrado de lado L. Para atender uma demanda específica, foi pedido a essa fábrica que dobrasse a medida do lado dessa tampa. Ao comparar-se a medida da superfície da nova peça com a peça antiga, a área da nova peça será
Alternativa B
Se a área era L², agora será de (2L)² = 4L², então, ao comparar essas duas áreas, podemos perceber que a nova área será 4 vezes maior.
-
Questão 8
Qual é a medida da diagonal de um quadrado que possui área igual a 196 cm²?
Alternativa C
Se a área do quadrado é 196, então, calculando o lado, temos que:
\(l^2=196\)
\(l=\sqrt{196}\)
\(l=14\)
A medida da diagonal é igual a:
\(d=l\sqrt2\)
\(d=14\sqrt2\ cm\)
-
Questão 9
(Enem) Um vidraceiro precisa construir tampos de vidro com formatos diferentes, porém com medidas de área iguais. Para isso, pede a um amigo que o ajude a determinar uma fórmula para o cálculo do raio R de um tampo de vidro circular com área equivalente à de um tampo de vidro quadrado de lado L.
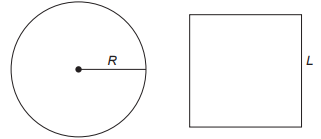
A fórmula correta é:
Alternativa A
Igualando as fórmulas da área de um círculo de raio R e a área do quadrado de lado L, temos que:
\(πR^2=L^2\)
Isolando R:
\(R^2=\frac{L^2}π\)
\(R=\sqrt\frac{L^2}{π}\)
\(R=\frac{L}{\sqrt\pi}\)
-
Questão 10
(Enem) Uma fábrica de fórmicas produz placas quadradas de lados de medida igual a y centímetros. Essas placas são vendidas em caixas com N unidades, e, na caixa, é especificada a área máxima S que pode ser coberta pelas N placas.
Devido a uma demanda do mercado por placas maiores, a fábrica triplicou a medida dos lados de suas placas e conseguiu reuni-las em uma nova caixa, de tal forma que a área coberta S não fosse alterada.
A quantidade X, de placas do novo modelo, em cada nova caixa será igual a:
Alternativa A
Sabemos que a área da primeira placa é igual ao lado ao quadrado, ou seja, y², e das novas placas é de (3y)² = 9y². Se anteriormente N placas cobriam a região S, sabemos que a área S coberta pelas placas era de Ny².
Agora, para calcular a quantidade X de placas, temos que:
\(X⋅9y^2=Ny^2\)
\(X=\frac{Ny^2}{9y^2}\)
\(X=\frac{N}9\)
-
Questão 11
(Enem) Uma indústria produz malhas de proteção solar para serem aplicadas em vidros, de modo a diminuir a passagem de luz, a partir de fitas plásticas entrelaçadas perpendicularmente. Nas direções vertical e horizontal, são aplicadas fitas de 1 milímetro de largura, tal que a distância entre elas é de (d – 1) milímetros, conforme a figura. O material utilizado não permite a passagem da luz, ou seja, somente o raio de luz que atingir as lacunas deixadas pelo entrelaçamento consegue transpor essa proteção. A taxa de cobertura do vidro é o percentual da área da religião coberta pelas fitas da mala, que são colocadas paralelamente às bordas do vidro.
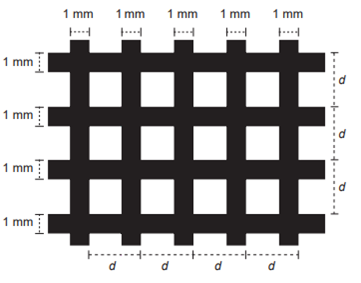
Essa indústria recebeu a encomenda de uma malha de proteção solar para ser aplicada em um vidro retangular de 5 m de largura por 9 m de comprimento. A medida de d, em milímetros, para que a taxa de cobertura da malha seja de 75%, é:
Alternativa A
Calculando a razão entre a área de incidência de luz e a área do quadrado, temos que:
\(\frac{(d-1)^2}{d^2} =25%\)
\(\big(\frac{(d-1)}{d^2}\big)=0,25\)
\(\frac{d-1}d=\sqrt{0,25}\)
\(\frac{d-1}d=0,5\)
\(d-1 = 0,5d\)
\(d-0,5d=1\)
\(0,5d=1\)
\(d=\frac{1}{0,5}\)
\(d=2\)
-
Questão 12
(Enem) Na zona rural, a utilização de unidades de medida como o hectare é bastante comum. O hectare equivale à área de um quadrado de lado igual a 100 metros. Na figura, há a representação de um terreno por meio da área em destaque. Nessa figura, cada quadrado que compõe a malha representa uma área de 1 hectare.
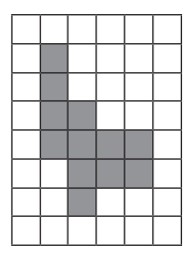
O terreno em destaque foi comercializado pelo valor R$ 3.600.000. O valor do metro quadrado desse terreno foi de
Alternativa A
Sabemos que a área do quadrado é igual ao quadrado do seu lado.
\(A=l^2\)
\(A=100^2\)
\(A=10.000\)
Contando na imagem, podemos perceber que há 12 quadrados, logo, essa área é de
12 ⋅ 10.000 = 1.200.000
Como foram pagos R$ 3.600.000, então o valor pago foi:
\(3.600.000∶1.200.000=30\)