Exercícios sobre área dos setores circulares
Estes exercícios sobre área dos setores circulares são resolvidos com base na fórmula da área do círculo, porém, adaptada para setores circulares.
Publicado por: Luiz Paulo Moreira SilvaQuestões
-
Questão 1
Um fazendeiro precisou construir uma parte de uma tampa de concreto para sua cisterna. Essa parte corresponde a uma semicircunferência, ou seja, ao setor circular de ângulo 180 graus. O diâmetro da cisterna é de 3 metros, conforme constatou o fazendeiro. Sabendo que o custo de construção dessa tampa é de R$100,00 por metro quadrado, qual o valor gasto?
Utilize a fórmula para cálculo da área do setor circular:
A = π · r2 · a
360A = 3,14 · 1,52 · 180 = 3,14 · 2,25 = 7,065 = 3,5325 m2
360 2 2Observe que o raio é 1,5m, já que o diâmetro é 3m. Uma vez que o metro quadrado custará R$100,00, basta multiplicar esse valor pela área da tampa da cisterna.
100,00 · 3,53 = 353,25
O Fazendeiro gastará R$353,25.
-
Questão 2
Qual a área de um setor circular de ângulo 30 graus, que tem um diâmetro de 10 metros?
Utilizando a fórmula, teremos:
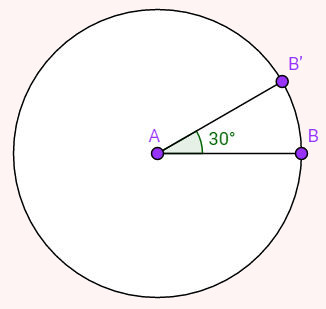
A = 3,14 · 52 · 30
360A = 3,14 · 25
12A = 78,5
12A = 6,54 m2
-
Questão 3
Calcule a área da região sombreada na figura a seguir:
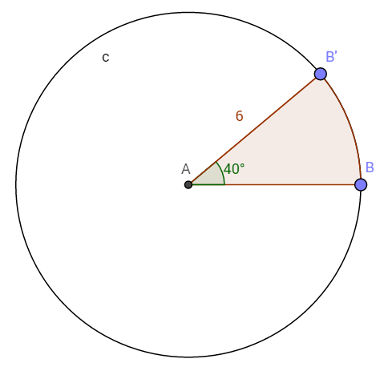
Utilizando a fórmula para cálculo de área, teremos a seguinte expressão:
A = 3,14 · 62 · 40
360A = 3,14 · 36
9A = 113,04
9A = 12,56 m2
-
Questão 4
(FATEC – 08) Na figura, o Raio do círculo de centro S é três vezes o raio do círculo de centro O, e os ângulos centrais sombreados, RST e POQ, são tais que a medida de RST é a metade da medida de POQ.
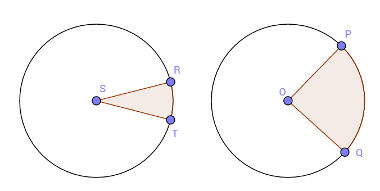
Se, no círculo de centro O, a área do setor circular sombreado POQ é igual a 4, então, no círculo de centro S, a área do setor circular sombreado RST é:
a) 6 b) 12 c) 18 d) 28 e) 30
Primeiramente, vamos organizar os dados do exercício.
i) Seja o raio do círculo de centro O = r, então o raio do círculo de centro S = 3r
ii) Seja “a” o ângulo do setor circular RST, então o ângulo do setor circular POQ é 2.a
iii) Sejam I e II as áreas dos setores circulares RST e POQ respectivamente.
iv) II = 4
v) A fórmula para calcular a área da região circular é A = π · r2 · a, onde r = raio do setor circular e a = ângulo do setor circular. 360
Agora basta substituir esses dados na fórmula da área. Mas isso deve ser feito de modo organizado para evitar erros. Observe os cálculos das áreas de RST e POQ respectivamente
I = π · a · (3 · r)2
360I = π · a · 9 · r2
360I = π · a · r2
4040 · I = π · a · r2
Por outro lado,
II = π · 2 · a · r2
360II = π · a · r2
180180 · II = π · a · r2
Logo,
40 · I = 180 · II
I = 180 · II
40Como II = 4,
I = 180 · 4 = 18
40