Exercícios sobre áreas de paralelogramos
Das alternativas a seguir, assinale a que for correta.
a) Um quadrado e um retângulo podem ter as medidas de suas áreas obtidas de forma igual.
b) As áreas do losango e do retângulo têm as medidas de suas áreas obtidas exatamente da mesma maneira.
c) A única maneira de calcular a área do losango é multiplicando a medida de sua base pela medida de sua altura.
d) A área de um quadrado pode ser obtida de diversas formas. Uma delas é multiplicando sua diagonal maior por sua diagonal menor.
e) A área de todos os paralelogramos é calculada exatamente da mesma maneira.
a) Correta!
Embora a fórmula mais conhecida para o cálculo da área do quadrado seja A = l2, essa área também pode ser obtida da mesma forma que a área dos retângulos (A = bh).
b) Incorreta!
A área do losango é o produto de suas diagonais dividido por 2, e a área do retângulo é igual ao produto das medidas de sua base por sua altura.
c) Incorreta!
A única maneira de calcular a área de um losango é multiplicando suas diagonais e dividindo o resultado por 2.
d) Incorreta!
A área do quadrado pode ser obtida de algumas formas diferentes, mas todas elas resultam no mesmo cálculo final, que é o produto de sua base pela sua altura.
e) Incorreta!
A área do retângulo e do paralelogramo são calculadas de forma igual. As áreas das outras figuras, não.
Gabarito: alternativa A.
A prefeitura de uma cidade gasta R$ 33,00 por metro quadrado de grama plantada. Sabendo que uma praça, que possui formato de losango, foi totalmente revestida com essa mesma grama e que as diagonais dessa praça medem 18 m e 22 m, responda: quanto a prefeitura gastou nessa obra?
a) R$ 198,00
b) R$ 396,00
c) R$ 1440,00
d) R$ 6500,00
e) R$ 6534,00
A área do losango é o produto de suas diagonais dividido por 2, portanto:
A = D·d
2
A = 18·22
2
A = 396
2
A = 198 m2
Para concluir o exercício, basta multiplicar a metragem da praça pelo valor gasto por metro quadrado:
33·198 = 6534
Assim, o total gasto com grama nessa praça foi de R$ 6534,00.
Gabarito: alternativa E.
(Saresp - modificada) A área do losango inscrito no retângulo é 20 m2. A diagonal menor do losango tem 5 m. Portanto, sua diagonal maior mede quantos metros?
a) 10 metros
b) 8 metros
c) 6 metros
d) 5 metros
e) 40 metros
Tendo em vista a fórmula para o cálculo da área do losango, basta substituir nela os valores dados pelo exercício. Observe:
A = D·d
2
20 = D·5
2
20·2 = D·5
40 = D·5
D = 40
5
D = 8 metros
Gabarito: alternativa B.
(Saresp - modificada) Se para cobrir cada m2 de telhado são usadas 20 telhas francesas, então, para cobrir um telhado com as dimensões indicadas na figura, serão necessárias quantas telhas?
a) 1000 telhas
b) 1200 telhas
c) 1600 telhas
d) 1800 telhas
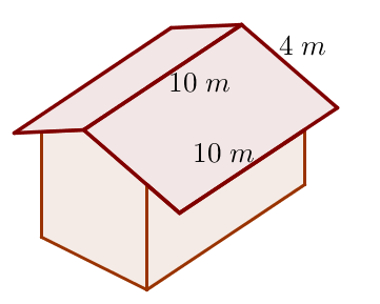
Para descobrir a quantidade de telhas, é necessário descobrir a metragem do telhado. Note que ele é formado por dois paralelogramos cujo comprimento mede 10 metros e a largura mede 4 metros. Assim, a área do telhado é igual a duas vezes a área do paralelogramo:
AT = 2·b·h
AT = 2·10·4
AT = 2·40
AT = 80 m2.
Agora, basta multiplicar esse resultado pelo número de telhas por metro quadrado:
20·80 = 1600 telhas
Gabarito: alternativa C.
