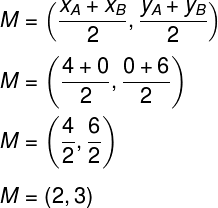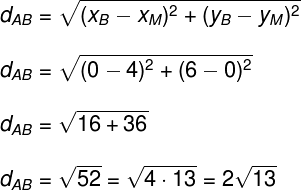Exercícios sobre cônicas
Com estes exercícios, é possível avaliar seus conhecimentos sobre as cônicas e obter as resoluções comentadas das questões.
Publicado por: Luiz Paulo Moreira SilvaQuestões
-
Questão 1
A respeito das definições básicas de circunferência e de elipse, qual das alternativas a seguir está correta?
a) Uma circunferência é o conjunto de pontos cuja distância até o ponto central C é constante e igual ao diâmetro.
b) Uma elipse é o conjunto de pontos cuja distância até o ponto central C é igual à constante r, chamada de raio.
c) Uma circunferência é o conjunto de pontos cuja soma das distâncias até os focos é igual a uma constante 2a.
d) Uma elipse é uma circunferência achatada.
e) Uma circunferência é um conjunto de pontos cuja distância até o ponto central C é igual à constante r, chamada de raio.
A definição de circunferência é um conjunto de pontos cuja distância até o ponto central C é igual a uma constante r, chamada de raio. A definição de elipse é: conjunto de pontos cuja soma das distâncias até os focos é igual à constante 2a.
Portanto, a alternativa correta é a letra E.
-
Questão 2
(UFAM) Os pontos A(4, 0) e B(0, 6) são extremos de um diâmetro da circunferência. Então, a equação reduzida da circunferência é:
a) x2 + y2 – 6x – 4y = 0
b) x2 + y2 – 4x – 6y = 0
c) x2 + y2 + 4x – 6y = 0
d) x2 + y2 + 4x + 6y = 0
e) x2 + y2 – 6x + 4y = 0
Letra B
Como o diâmetro da circunferência é igual ao dobro do raio, então devemos encontrar as coordenadas do centro da circunferência e, depois, calcular o comprimento de seu raio. Para achar as coordenadas do centro, descobriremos o ponto médio do segmento AB:
Para encontrar o comprimento do raio, basta calcular o comprimento do diâmetro e dividi-lo por 2:
O raio dessa circunferência é metade da distância de A até B, portanto:
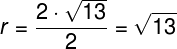
Tendo em mãos a medida do raio às coordenadas do centro, a equação reduzida da circunferência e o desenvolvimento de seus termos será:
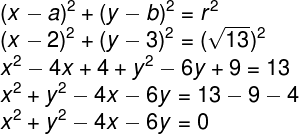
-
Questão 3
(PUC-Rio) O número de pontos de intersecção das duas parábolas y = x2 e y = 2x2 – 1 é:
a) 0
b) 1
c) 2
d) 3
e) 4
Para encontrar os pontos de intersecção entre duas figuras, é necessário igualar suas equações. Como as equações das duas parábolas já estão em função de x, podemos fazer:
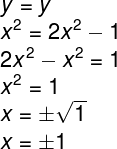
Substituindo esses valores nas funções, teremos:
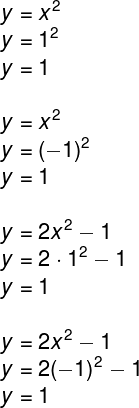
Assim, os pontos tanto na primeira função quanto na segunda são:
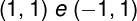
Logo, são apenas dois pontos.
Letra C.
-
Questão 4
Uma hipérbole é uma figura geométrica plana formada pelo conjunto dos pontos cujo módulo da diferença das distâncias entre eles e os focos é igual à constante 2a. Em outras palavras: dado o ponto P (a distância entre P e o primeiro foco e a distância entre P e o segundo foco), hipérbole é o conjunto dos pontos cuja diferença entre as medidas dessa distância sempre tem 2a como resultado. A respeito das hipérboles, assinale a alternativa que contém uma das suas equações reduzidas.
a) a2 – b2 = 1
x2 y2b) (x – a)2 + (y – b)2 = 1
c) x2 – y2 = 1
a2 b2d) x2 + y2 = 1
a2 b2e) NDA.
Das equações apresentadas, a única que representa a equação reduzida da hipérbole é a letra C.