Exercícios sobre Diagrama de Venn
(ESAL) Foi consultado um certo número de pessoas sobre as emissoras de TV que habitualmente assistem. Obteve-se o resultado seguinte: 300 pessoas assistem ao canal A, 270 pessoas assistem ao canal B, das quais 150 assistem ambos os canais A e B e 80 assistem a outros canais distintos de A e B. O número de pessoas entrevistadas foi:
a) 800
b) 720
c) 570
d) 500
e) 600
Sabemos que 150 pessoas assistem ao canal A e ao canal B, logo, esse é o número que ocupará a posição central dos dois círculos grandes, chamada de interseção de A com B. O número de pessoas que assistem ao canal A é 300 no total. Devemos colocar apenas 150 pessoas dentro do círculo roxo, pois esse é o número de pessoas que assistem exclusivamente ao canal A. Note que o número de pessoas que assistem exclusivamente ao canal A somado ao número de pessoas que assistem tanto o canal A quanto o canal B é 300.
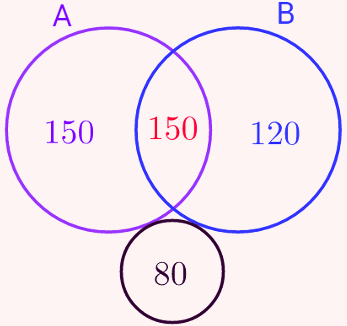
Repita o processo para descobrir quantas pessoas assistem exclusivamente ao canal B e, fora desses círculos, coloque um terceiro círculo para indicar as pessoas que não assistem nem ao canal A nem ao canal B.
Agora basta somar os números dentro do diagrama para obter a quantidade de pessoas entrevistadas.
150 + 150 +120 + 80 = 500
Gabarito: Letra D.
(UNICAMP-2009) Três candidatos A, B e C concorrem à presidência de um clube. Uma pesquisa apontou que, dos sócios entrevistados, 150 não pretendem votar. Dentre os entrevistados que estão dispostos a participar da eleição, 40 sócios votariam apenas no candidato A, 70 votariam apenas em B, e 100 votariam apenas no candidato C. Além disso, 190 disseram que não votariam em A, 110 disseram que não votariam em C, e 10 sócios estão na dúvida e podem votar tanto em A como em C, mas não em B. Finalmente, a pesquisa revelou que 10 entrevistados votariam em qualquer candidato. Com base nesses dados, pergunta-se:
a) Quantos sócios entrevistados estão em dúvida entre votar em B ou em C, mas não votariam em A? Dentre os sócios consultados que pretendem participar da eleição, quantos não votariam em B?
b) Quantos sócios participaram da pesquisa? Suponha que a pesquisa represente fielmente as intenções de voto de todos os sócios do clube. Escolhendo um sócio ao acaso, qual a probabilidade de que ele vá participar da eleição mas ainda não tenha se decidido por um único candidato?
Para construir o diagrama de Venn desse exercício, devemos analisá-lo parte a parte. A primeira informação é de que 150 pessoas não pretendem votar. O círculo laranja representa-os. As pessoas que já têm seus votos definidos são colocadas no interior dos respectivos círculos: 40 no círculo do candidato A, 70 no círculo do candidato B e 100 no círculo do candidato C.
As interseções entre dois candidatos devem ser feitas com cuidado. Como 190 pessoas disseram que não votariam no candidato A, diminuímos de 190 as 70 pessoas que votarão no candidato B e as 100 pessoas que votarão no candidato C.
190 – 70 – 100 = 20
Essas 20 pessoas são aquelas que votam em B ou em C. Portanto, na interseção de B com C, colocamos o número 20.
Seguindo o mesmo raciocínio, encontramos 0 pessoas indecisas entre A e B.
Contudo, 10 sócios disseram que votariam em qualquer candidato entre A e C, mas não em B. Logo, a interseção entre A e C deve ser preenchida com o número 20.
Por fim, 10 pessoas disseram que votariam em qualquer candidato. Então, o espaço central, que é a interseção entre A, B e C, deve ser preenchido com o número 10.
Todo esse processo resultará no seguinte diagrama de Venn:
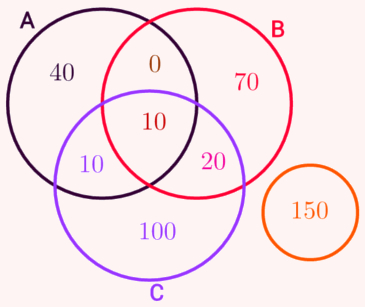
a) O número de sócios em dúvida entre os candidatos B e C que não votariam em A é igual a 20 e o número de pessoas que não votariam em B é a soma dos números fora do círculo vermelho (exceto as pessoas que não pretendem votar).
40 + 10 + 100 = 150
b) Para encontrar o número de sócios que participaram da pesquisa, basta somar todos os números que aparecem no diagrama de Venn:
40 + 0 + 70 + 10 + 10 + 20 + 100 + 150 = 400
Já a probabilidade de que o sócio que vai participar da eleição ainda não tenha escolhido um candidato é dada pelo número de pessoas em qualquer interseção dividido pelo número total de pessoas:
40 = 1
400 10
Qual das alternativas abaixo está incorreta quanto aos conjuntos numéricos e sua representação no diagrama de Venn?
a) Os números reais são definidos como o conjunto numérico que contém todos os números racionais e irracionais.
b) No diagrama de Venn, os números racionais são representados por uma figura geométrica que contém outra figura que representa o conjunto dos números inteiros.
c) No diagrama de Venn, o conjunto dos números naturais é representado por uma figura geométrica que é a única a estar dentro de todos os outros conjuntos.
d) O conjunto dos números naturais não contém nenhum outro conjunto numérico em sua totalidade, exceto por seus próprios subconjuntos.
e) O conjunto dos números irracionais não contém nenhum outro conjunto numérico, exceto por seus próprios subconjuntos e, além disso, costuma ser representado por um retângulo, lado a lado ao retângulo que representa os números racionais.
a) Verdadeira.
b) Verdadeira.
c) Falsa.
No diagrama de Venn, o conjunto dos números naturais geralmente é representado por um círculo que está dentro do conjunto dos números inteiros. Esse último, por sua vez, também é representado por um círculo, que está dentro do conjunto dos números racionais, que é representado por um retângulo. Esse retângulo fica lado a lado com outro, que representa o conjunto dos números irracionais. Logo, o conjunto dos números naturais não possui representação dentro do conjunto dos irracionais. Portanto, a questão está incorreta.
d) Verdadeira.
e) Verdadeira.
Qual das afirmações abaixo está correta com relação às representações por Diagrama de Venn dos conjuntos dos números naturais, pares e ímpares?
a) Existem elementos na interseção dos números pares com os números ímpares, isto é, existem números que são pares e ímpares ao mesmo tempo.
b) O conjunto dos números pares contém o conjunto dos números ímpares.
c) O conjunto dos números ímpares contém o conjunto dos números pares.
d) O conjunto dos números naturais contém apenas o conjunto dos números pares
e) O conjunto dos números naturais contém os conjuntos dos números pares e dos números ímpares, que, por sua vez, não possuem nenhum elemento em comum.
a) Falsa.
O conjunto dos números pares e o conjunto dos números ímpares não possuem nenhum elemento em comum. Ou um número é par, ou um número é impar, não é possível que seja os dois ao mesmo tempo.
b) Falsa.
O conjunto dos números ímpares não contém o conjunto dos números pares, pois, nesse caso, haveria elementos pares e ímpares ao mesmo tempo.
c) Falsa.
O conjunto dos números pares também não contém o conjunto dos números ímpares pelo mesmo motivo da alternativa anterior.
d) Falsa!
O conjunto dos números naturais é composto por todos os inteiros maiores que zero. Logo, 1, que é um número ímpar, pertence ao conjunto dos naturais. Portanto, ele não contém apenas números pares.
e) Verdadeira.
