Exercícios sobre Equação do 2º Grau
Teste os seus conhecimentos: Faça exercícios sobre Equação do 2º Grau e veja a resolução comentada.
Publicado por: Raul Rodrigues de OliveiraQuestões
-
Questão 1
Analisando a equação do segundo grau x² – 2x +1 = 0, podemos afirmar que ela possui:
Resolução
Alternativa B.
Para encontrar o número de soluções reais de uma equação do 2º grau, é necessário encontrar o valor do discriminante (delta). Para isso, encontraremos primeiro o valor dos coeficientes a, b e c na equação:
a = 1
b = -2
c = 1
Agora vamos calcular o valor de delta:
Δ = b² – 4ac
Δ = (-2)² – 4 ·1·1
Δ = 4 – 4
Δ = 0
O valor de delta mostra o número de soluções da equação, sem ter a necessidade de calcular os valores dessas raízes. Como Δ = 0, a equação possui uma única solução real.
-
Questão 2
Uma região retangular teve as suas dimensões descritas em metros, conforme a imagem a seguir:
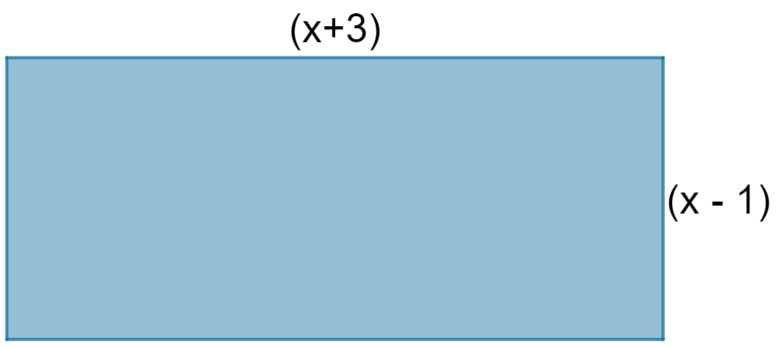
O valor de x que faz com que a área dessa região seja igual a 21 é:
Resolução
Alternativa D.
A área de um retângulo é calculada pelo produto entre as medidas de seus lados, então:
(x + 3) ( x – 1) = 21
Aplicando a propriedade distributiva, temos que:
x² – 1x +3x – 3 = 21
x² +2x – 3 = 21
Para que seja possível aplicar a fórmula de Bhaskara, vamos igualar a equação a zero:
x² + 2x – 3 – 21 = 0
x² + 2x – 24 = 0
Os coeficientes da equação são:
a = 1
b= 2
c = - 24
Calculando o valor de delta, temos que:
Δ = b² – 4ac
Δ = (2)² – 4 ·1·(-24)
Δ = 4 + 96
Δ = 100
Aplicando a fórmula de Bhaskara, encontraremos:
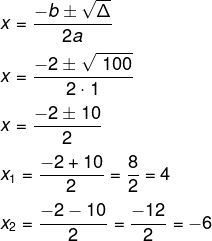
Note que o valor x = -6 faria com que os lados do retângulo fossem valores negativos, logo, entre as soluções da equação, a única que faz sentido é x = 4.
-
Questão 3
Uma equação foi descrita da seguinte maneira:
(k² – 4) x³ + ( k – 2 )x² + 7x - 8 = 0
Analisando os coeficientes, o valor de k que faz com que essa equação seja uma equação do 2º grau é:
Resolução
Alternativa C.
Para que essa equação seja do 2º grau, o coeficiente de x³ tem que ser igual a zero, e o coeficiente de x² tem que ser diferente de zero, ou seja:
Condição I:
k² – 4 = 0
k² = 4
k = ±√4
k = ± 2
Logo, para satisfazer a primeira condição, temos k = 2 ou k = -2.
Agora vamos analisar a segunda condição.
Condição II:
k – 2 ≠ 0
k ≠ 2.
O valor que satisfaz ambas as condições é k = -2.
-
Questão 4
Das equações quadráticas abaixo e sabendo que a = 1, qual é a equação que possui as soluções x1 = 2 e x2 = - 3?
Resolução
Alternativa A.
Conhecendo as soluções da equação, temos que:
a(x – x1) (x – x2) = 0
Substituindo os valores dados, temos que:
1·( x – 2 ) ( x - (-3)) = 0
(x – 2 ) ( x + 3) = 0
x² +3x – 2x – 6 = 0
x² + x – 6 = 0
-
Questão 5
O produto entre as raízes da equação 2x² + 4x - 6 = 0 é igual a:
Resolução
Alternativa E.
Pela fórmula da soma e produto, temos que:
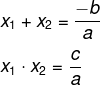
Vamos analisar os coeficientes da equação:
2x² + 4x - 6 = 0
a = 2
b = 4
c = -6
Utilizando somente a segunda equação, temos que:
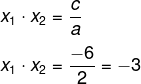
Logo, o produto entre as raízes da equação é -3.
-
Questão 6
Utilizando seus conhecimentos sobre equação do segundo grau, julgue as afirmativas a seguir como verdadeiras ou falsas.
I – Toda equação do segundo grau possui pelo menos uma solução real.
II – Uma equação do segundo grau é conhecida como incompleta quando o coeficiente b ou c é igual a zero.
III – Quando o valor do discriminante é um número positivo que não possui raiz quadrada exata, dizemos que a equação não possui solução.
Analisando as afirmativas, podemos afirmar que:
Resolução
Alternativa B.
Vamos analisar cada uma das afirmativas.
I – Falsa. Nem sempre a equação do segundo grau possui solução. Uma forma de verificar se a equação possui solução nos números reais é calcular o delta. Caso ele seja negativo, a equação não possui solução real.
II — Verdadeira. Por definição, a equação é incompleta quando b = 0 ou quando c = 0.
III – Falsa. Quando o valor do discriminante é positivo, há duas soluções reais na equação, independentemente de ele possuir raiz quadrada exata ou não.
-
Questão 7
Dada a equação -x² -4x +5 = 0, podemos afirmar que o conjunto de soluções dessa equação é:
Resolução
Alternativa C.
Queremos encontrar as soluções da equação -x² -4x +5 = 0.
Para calcular o valor de delta, temos que:
a = - 1 b = -4 e c = 5
Δ = (-4)² -4·(-1)·5
Δ = 16 + 4 ·5
Δ = 16 + 20
Δ = 36
Agora utilizando a fórmula de Bhaskara, temos que:
-
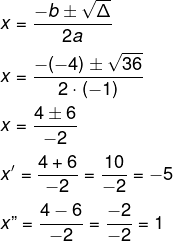
Questão 8
A multiplicação entre a idade de Kárita e a idade de Karla é igual a 374. Kárita é 5 anos mais velha que Karla. Quantos anos Karla e Kárita possuem respectivamente?
Resolução
Alternativa B.
Seja x a idade da Karla, então, como Kárita é 5 anos mais velha, a sua idade pode ser representada por x+5. Sabemos que o produto da idade delas é igual a 374, então temos que:
x (x+5) = 374
Aplicando a propriedade distributiva:
x² + 5x = 374
Igualando a equação a zero, teremos:
x² + 5x – 374 = 0
a = 1 b = 5 c = – 374
Δ = b² – 4.a.c
Δ = 5² – 4.1. (– 374)
Δ = 25 + 1496
Δ = 1521
Agora utilizando a fórmula de Bhaskara, temos que:
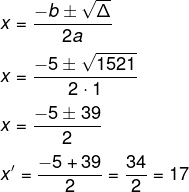
Note que x” resultaria em um valor negativo, o que faz com que ele não seja solução do problema, pois não existe idade negativa.
Como x é a idade da Karla, ela possui 17 anos.
Já a Kárita possui x+5, ou seja, 17 + 5 = 22 anos.
-
Questão 9
(Enem 2013) A temperatura T de um forno (em graus centígrados) é reduzida por um sistema a partir do instante de seu desligamento (t = 0) e varia de acordo com a expressão T(t) = -t²/4 +400, com t em minutos. Por motivos de segurança, a trava do forno só é liberada para abertura quando o forno atinge a temperatura de 39°C.
Qual o tempo mínimo de espera, em minutos, após se desligar o forno, para que a porta possa ser aberta?
Resolução
Alternativa D.
Devido à trava, o forno pode ser aberto somente quando ele atinge 39 ºC, então faremos T(t) = 39.
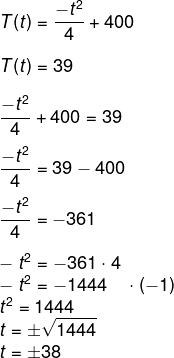
Como t é tempo, então ele é necessariamente positivo, ou seja, t = 38 minutos.
-
Questão 10
(Fatec) Se a equação x² - 10x + k = 0 tem uma raiz de multiplicidade 2, então o valor de k é
Alternativa B.
Para que uma raiz tenha multiplicidade 2, a equação precisa ter uma única solução, ou seja, Δ = 0. Vamos calcular o valor de Δ na equação x² - 10x + k = 0, em que a=1 b= -10 e c = k.
Δ = b² – 4ac
Δ = (-10)² – 4 ·1·k
Δ = 100 – 4k
Mas Δ= 0, então:
100 – 4k = 0
100 = 4k
100 : 4 = k
25 = k
Logo, k = 25 é o valor que faz com que a equação tenha uma solução de multiplicidade 2.
-
Questão 11
(Enem 2010) Um laticínio possui dois reservatórios de leite. Cada reservatório é abastecido por uma torneira acoplada a um tanque resfriado. O volume, em litros, desses reservatórios depende da quantidade inicial de leite no reservatório e do tempo t, em horas, em que as duas torneiras ficam abertas. Os volumes dos reservatórios são dados pelas funções V1(t) = 250t³ - 100t + 3000 e V2(t) = 150t³ + 69t + 3000.
Depois de aberta cada torneira, o volume de leite de um reservatório é igual ao do outro no instante t = 0 e, também, no tempo t igual a
Resolução
Alternativa A.
Para que o volume seja igual, faremos:
V1(t) = V2(t)
250t³ - 100t + 3000 = 150t³ + 69t + 3000
Podemos isolar a incógnita t e encontraremos:
250t³ – 150 t³ – 100t – 69t = 3000 – 3000
100t³ -169t = 0
Colocando t em evidência, temos que:
t (100t² – 169) = 0
Sabemos que uma multiplicação é zero quando um dos seus fatores é zero, ou seja:
(I) t = 0 (solução já apresentada no enunciado) ou (II) 100t² – 169 = 0
Resolvendo o caso II, temos que:
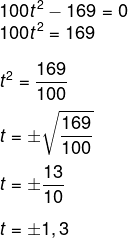
Como t representa o tempo, então descartaremos a opção negativa, logo temos t = 1,3.
-
Questão 12
(UERGS) Sendo S a soma e P o produto das raízes da equação 2x² − 5x − 7 = 0, pode-se afirmar que:
Resolução
Alternativa A.
Dada a equação 2x² − 5x − 7 = 0, sabemos que a soma e o produto das raízes podem ser calculados da seguinte maneira:
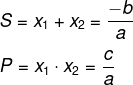
Os coeficientes da equação são:
a = 2
b = -5
c= -7
Então, a soma S e o produto P serão:
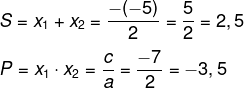
Agora, sabendo que S = 2,5 e P = -3,5 e analisando as afirmativas, é possível verificar que a alternativa A é a correta, pois:
S – P = 6
2,5 - (-3,5) = 6
2,5 + 3,5 = 6