Exercícios sobre equação do 2º grau incompleta
Esta lista contém questões sobre equação do 2º grau incompleta para que você teste seus conhecimentos treinando os diferentes métodos de resolução dessas equações.
Publicado por: Raul Rodrigues de OliveiraQuestões
-
Questão 1
Dada a equação do 2º grau a seguir, podemos afirmar que o conjunto de soluções dessa equação é igual a:
2x² – 8 = 0
A) S = {-2, 2}
B) S = {-4, 4}
C) S = {-1, 1}
D) S = {0, 4}
E) S = {0, 2}
Alternativa A
Isolando a incógnita x, temos que:
2x² = 8
x² = 8 : 2
x² = 4
x = ±√4
x = ±2
-
Questão 2
Ao fazer o lançamento de um móvel, o físico descreveu que a relação entre distância e altura pode ser dada pela função d(t) = -4t² + 24t. Sendo assim, sabendo que ele parte da distância zero, a distância percorrida por esse móvel até atingir d(t) = 0 novamente será de:
A) 2 segundos
B) 3 segundos
C) 4 segundos
D) 5 segundos
E) 6 segundos
Alternativa E
Queremos encontrar o valor de t, tal que -4t² + 24t = 0.
Colocando t em evidência, temos que:
t (-4t + 24) = 0
Sabemos que t = 0 é uma das soluções, mas não é a procurada. Então, além de t = 0, temos que:
-4t + 24 = 0
-4t = -24
t = -24 : (-4)
t = 6 segundos
-
Questão 3
Analise as expressões algébricas a seguir e marque a alternativa que corresponde a uma equação do 2º grau incompleta.
A) 2x² + 4x = 2
B) 3x² > 0
C) x² – 8x + 1 = 0
D) x² – 3x + 4 = 4
E) x² + 1 > x
Alternativa D
A única alternativa que contém uma equação incompleta é a alternativa D, pois é possível simplificar a expressão:
x² – 3x + 4 = 4
x² – 3x + 4 – 4 = 0
x² – 3x = 0
-
Questão 4
Uma equação do 2º grau é considerada incompleta quando
A) possui uma única solução.
B) os coeficientes b ou c são iguais a zero.
C) não possui soluções reais.
D) possui coeficientes negativos.
Alternativa B
Para que uma equação do 2º grau seja considerada incompleta, é necessário que um de seus coeficientes, b ou c, ou os dois ao mesmo tempo, seja igual a zero.
-
Questão 5
Dada a equação x² – 25 = 0, com soluções no conjunto dos números reais, julgue as afirmativas a seguir:
I → A soma das soluções da equação é igual a zero.
II → O conjunto de soluções é S{-5, 5}.
III → Essa equação é incompleta.
A) Somente I é falsa.
B) Somente II é falsa.
C) Somente III é falsa.
D) Todas são verdadeiras.
E) Todas são falsas.
Alternativa D
Resolvendo a equação, temos que:
x² – 25 = 0
x² = 25
x = ±√25
x = ±5
Agora vejamos cada uma das afirmativas:
I → A soma das soluções da equação é igual a zero. (verdadeira)
-5 + 5 = 0
II → O conjunto de soluções é S{-5, 5}. (verdadeira)
As possíveis soluções são -5 e 5.
III → Essa equação é incompleta. (verdadeira)
Temos b = 0, logo, essa equação é incompleta.
-
Questão 6
Durante a resolução de problemas, foi encontrada uma equação do tipo ax² = 0, sabendo que a ≠ 0, então, o número de soluções distintas que essa equação possui é igual a:
A) 0
B) 1
C) 2
D) 3
E) 4
Alternativa B
Temos que ax² = 0. Como a é diferente de 0, então, temos que:
x² = 0 : a
x² = 0
x = ±√0
x = 0
Então podemos afirmar que essa equação possui somente uma solução, ou seja, o número de soluções distintas dela é 1.
-
Questão 7
(Enem) A temperatura T de um forno (em graus centígrados) é reduzida por um sistema a partir do instante de seu desligamento (t = 0) e varia de acordo com a expressão T(t) = -t²/4 + 400, com t em minutos. Por motivos de segurança, a trava do forno só é liberada para abertura quando o forno atinge a temperatura de 39 °C.
Qual o tempo mínimo de espera, em minutos, após se desligar o forno, para que a porta possa ser aberta?
A) 19,0
B) 19,8
C) 20,0
D) 38,0
E) 39,0
Alternativa D
Devido à trava, o forno pode ser aberto somente quando ele atinge 39 ºC, então faremos T(t) = 39.
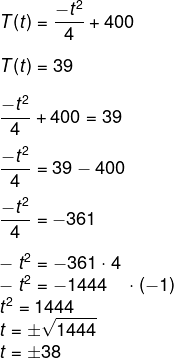
Como t é tempo, então ele é necessariamente positivo, ou seja, t = 38 minutos.
-
Questão 8
A área de um círculo é igual a 19,375 cm². Sabendo que a área do círculo é dada pela equação A = πr² e admitindo π = 3,1, então, o valor do raio desse círculo é igual a:
A) 2,0 cm
B) 2,2 cm
C) 2,5 cm
D) 2,7 cm
E) 3,0 cm
Alternativa C
Sabemos que A = πr². Substituindo os valores conhecidos, temos A = 19,375 e π = 3,1, então, temos que:
19,375 = 3,1 r²
19,375 : 3,1 = r²
6,25 = r²
r² = 6,25
r = √6,25
r = 2,5 cm
-
Questão 9
Conhecendo a equação incompleta 2x² – 4x = 0, sejam x1 e x2 as soluções da equação, com x1 > x2, então o valor da expressão 3x1 + 2x2 é igual a:
A) 4
B) 5
C) 6
D) 7
E) 8
Alternativa C
Para encontrar o conjunto de soluções da equação, vamos colocar 2x em evidência:
2x (x – 2) = 0
2x = 0
x = 0 : 2
x = 0
ou
x – 2 = 0
x = 2
Então, temos que x1 = 2 e x2 = 0:
3x1 + 2x2
3 · 2 + 2 · 0
6 + 0
6
-
Questão 10
Em uma equação do tipo ax² + bx = 0, a solução mais simples, conhecida como trivial, é igual a 0 sempre. A outra solução dessa equação pode ser calculada por:
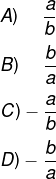
Alternativa D
Colocando x em evidência, temos que:
x(ax + b) = 0
Então x = 0 é a solução trivial, a outra é que:
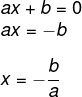
-
Questão 11
Analise as equações a seguir:
I → 2x² + 3x – 0 = 0
II → x² + 3 = 2x
III → x² + x – 1 = 0
São consideradas equações do 2º grau incompletas:
A) Somente I
B) Somente II
C) Somente III
D) Somente I e II
E) Somente II e III
Alternativa A
Na equação I, temos que c = 0, o que faz com que ela seja considerada uma equação do 2º grau incompleta.
-
Questão 12
Dadas as inequações x² + 4x = 0 e 2x² – 18 = 0, a soma das raízes não nulas delas é igual a:
A) -4B) -3
C) 0
D) 3
E) 2
Alternativa A
Primeiro encontraremos as soluções da equação x² + 4x = 0:
x² + 4x = 0
x(x + 4) = 0
x = 0 ou x + 4 = 0
x + 4 = 0
x = -4
Agora, encontraremos as soluções da equação 2x² – 18 = 0:
2x² – 18 = 0
2x² = 18
x² = 18 : 2
x² = 9
x = ±√9
x = ±3
Então a soma das raízes das equações é -4 + 3 – 3 = -4.