Exercícios sobre Equações Algébricas Fracionárias
Resolva a equação fracionária, sendo x ≠ 0:
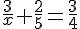
Temos a seguinte equação:
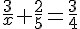
Primeiramente, vamos calcular o mínimo múltiplo comum (MMC) entre os denominadores da equação:
x, 5, 4 | 2
x, 5, 2 | 2
x, 5 , 1| 5
x , 1, 1| x
1, 1, 1| 2 . 2 . 5 . x = 20x
Agora que encontramos o MMC, nós utilizaremos o 20x como denominador, dividindo-o por cada denominador, e multiplicaremos o quociente pelo seu respectivo denominador:
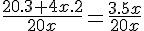
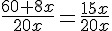
Multiplicando ambos os lados da equação pelo mesmo valor dos denominadores (20x), teremos:
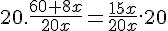
Podemos então cancelar o “20x” do denominador com o “20x” que acrescentamos dos dois lados, ficará apenas:
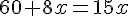
Resolvendo essa equação, temos:
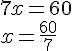
Portanto, x = 60/7.
Uma confecção produzia diariamente 200 calças. Após a contratação de 20 costureiras, a fábrica passou a produzir 240 calças. Quantas costureiras trabalhavam nessa confecção antes dessa contratação?
Vamos montar um quadro com as informações dadas no enunciado:
|
|
Antes da contratação |
Depois da contratação |
|
N° de calças |
200 |
240 |
|
N° de costureiras |
x |
x + 20 |
Organizando essas informações como uma regra de três simples e realizando a multiplicação cruzada, teremos:
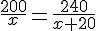
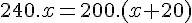
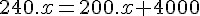
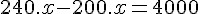
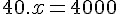
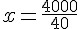
Encontramos então que x = 100.
Antes da contratação, havia 100 costureiras, e, depois da contratação, a confecção passou a ter 120 costureiras.
(UPE 2010) Sabendo que 
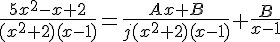para quaisquer valores reais da variável x diferente de 1 e que A e B são ambos números reais, é CORRETO afirmar que:
a) A + B = 5
b) A – B = 5
c) B – A = 2
d) A + B = 0
e) A – B = 2
Apesar de essa ser uma questão que envolve equações algébricas fracionárias, nós conseguimos obter um método alternativo para resolver esse exercício através de princípios do cálculo de polinômios. Inicialmente, vamos encontrar o mínimo múltiplo comum entre os denominadores x2 + 2 e x – 1, o qual será justamente o produto desses dois:
.jpg "Passo 1")
No numerador do segundo membro da equação, vamos utilizar a propriedade distributiva, ficando, portanto, com:
Ao agrupar os termos semelhantes no numerador do segundo membro e utilizar a ideia de fatoração, colocaremos em evidência o termo que mais se repetir:
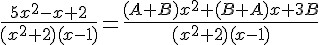
Como os denominadores são iguais, podemos desconsiderá-los. Vamos analisar apenas os numeradores:
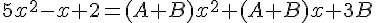
Se analisarmos os coeficientes da equação de segundo grau do lado esquerdo, esses devem ser necessariamente idênticos aos que estão do lado direito da equação, isto é, quem acompanha o termo x2 em um lado da equação deve ser igual a quem acompanha o x2 do outro lado, portanto, temos que:
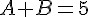
A resposta correta é a alternativa a.
(INTEGRADO RJ 1997 - adaptado) Encontre a solução de 
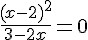
Primeiramente, vamos analisar a condição de existência dessa equação:
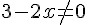
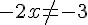
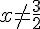
Podemos passar o termo do denominador do primeiro membro da equação para o outro lado, multiplicando-o por zero:
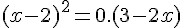
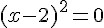
Extraindo a raiz quadrada de ambos os lados da equação, teremos:
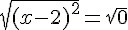
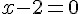
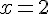
Portanto x = 2.
