Exercícios sobre equações irracionais
Ao resolver exercícios sobre equações irracionais, trabalhamos com igualdades em que a incógnita aparece no interior de raízes.
Publicado por: Amanda Gonçalves RibeiroQuestões
-
Questão 1
Resolva a equação irracional a seguir:
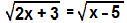
Uma alternativa para resolver equações irracionais é elevar ambos os lados da equação ao quadrado. Veja:
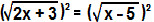
2x + 3 = x – 5
2x – x = – 5 – 3
x = – 8Portanto, a equação
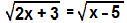apresenta uma única raiz: x = – 8. -
Questão 2
Na equação irracional
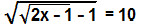, determine o valor de x.Vamos elevar os dois lados da equação ao quadrado:
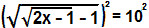
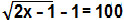
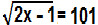
Repetiremos o mesmo processo:
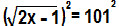
2x – 1 = 10201
2x = 10202
x = 10202
2
x = 5101A solução da equação irracional
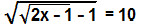é x = 5101. -
Questão 3
(UTFPR) A equação irracional
resulta em x igual a:Para resolver essa equação irracional, vamos elevar os dois lados da equação ao expoente 2:
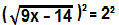
9x – 14 = 4
9x = 4 + 14
9x = 18
x = 18
9
x = 2Portanto, a alternativa correta é a letra e.
-
Questão 4
(MACK) Dado m > 0, a equação
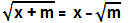admite:Para resolver essa equação irracional, vamos elevar os dois membros da equação ao quadrado, lembrando que, no segundo membro, será necessário aplicar o produto notável do quadrado da diferença.
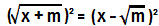
x + m = x² – 2 · x · √m + (√m)²
x + m = x² – 2x√m + m
x² – 2x√m – x = 0
x² – x · (2√m + 1) = 0Agora vamos utilizar a fórmula de Bhaskara. Os coeficientes da equação são a = 1, b = - 2√m + 1 e c = 0.
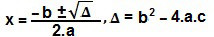
Δ = (-2√m + 1)² – 4.1.0
Δ = (-2√m + 1)² – 0
Δ = (-2√m + 1)²x = – (–2√m + 1) ± √(2√m + 1)²
2.1x = (2√m – 1) ± (2√m + 1)
2x' = 2√m + 1 + 2√m + 1 = 2√m + 2
2x'' = 2√m + 1 – 2√m – 1 = 0
2