Exercícios sobre estatística
(Enem PPL 2022 — reaplicação) Até a Copa de 2010, apenas sete jogadores haviam conseguido o feito de marcar 8 ou mais gols em uma mesma edição da Copa do Mundo. O quadro apresenta os anos das edições da Copa nas quais ocorreram esses feitos, quais foram os jogadores que os realizaram e os respectivos números de gols marcados por cada um deles.
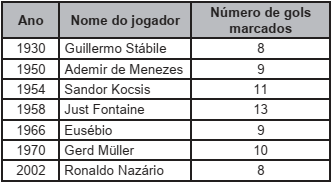
Para facilitar a análise sobre a quantidade de gols marcados por esses artilheiros nas referidas copas, foi calculada a mediana da distribuição dos números de gols marcados por eles nas sete copas especificadas no quadro.
A mediana dessa distribuição é igual a
A) 9,0.
B) 9,7.
C) 10,0.
D) 10,2.
E) 13,0.
Alternativa A
Para encontrar a mediana, colocaremos os dados em ordem:
8 8 9 9 10 11 13
Sabemos que a mediana é o termo que está posicionado no centro. Como há 7 elementos, a mediana é o 4º valor:
8 8 9 9 10 11 13
Assim, a mediana desse conjunto de dados é 9.
(Enem PPL 2010) Em uma corrida de regularidade, a equipe campeã é aquela em que o tempo dos participantes mais se aproxima do tempo fornecido pelos organizadores em cada etapa. Um campeonato foi organizado em 5 etapas, e o tempo médio de prova indicado pelos organizadores foi de 45 minutos por prova. No quadro, estão representados os dados estatísticos das 5 equipes mais bem classificadas.
Dados estatísticos das equipes mais bem classificadas (em minutos):
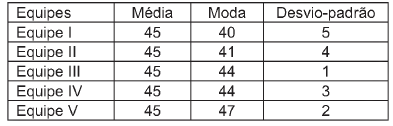
Utilizando os dados estatísticos do quadro, a campeã foi a equipe
A) I.
B) II.
C) III.
D) IV.
E) V.
Alternativa C
Sabemos que quanto menor é o desvio padrão, mais regulares são os dados. Note que todas possuem a mesma média, entretanto a equipe III é a que tem o menor desvio padrão. Logo, essa é a equipe que possui o tempo mais próximo da meta.
(UFT-TO) A nota final para uma disciplina de uma instituição de ensino superior é a média ponderada das notas A, B e C, cujos pesos são 1, 2 e 3, respectivamente. Paulo obteve A = 3,0 e B = 6,0. Quanto ele deve obter em C para que sua nota final seja 6,0?
A) 7,0
B) 9,0
C) 8,0
D) 10,0
Alternativa A
Seja x a terceira nota, temos que:
\(\overline{x}=\frac{1\cdot3+2\cdot6+3x}{1+2+3}\)
\(6=\frac{3+12+3x}{6}\)
\(6\cdot6=15+3x\)
\(36=15+3x\)
\(36-15=3x\)
\(21=3x\)
\(x=\frac{21}{3}\)
\(x=7\)
(Enem 2015) Uma pessoa, ao fazer uma pesquisa com alguns alunos de um curso, coletou as idades dos entrevistados e organizou esses dados em um gráfico.
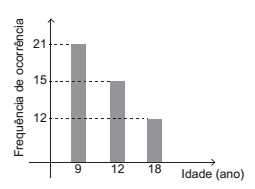
Qual a moda das idades, em anos, dos entrevistados?
A) 9
B) 12
C) 13
D) 15
E) 21
Alternativa A
A moda é o valor com maior frequência, ou seja, o valor que mais ocorreu. Analisando o gráfico, vemos que o valor que possui a maior ocorrência é a idade de 9 anos, que apareceu 21 vezes. Sendo assim, a moda desse conjunto é 9.
Buscando fazer uma renda extra, Fabrício decidiu fazer bolo no pote em sua casa para vender na escola. Antes de começar a produzir, ele resolveu fazer uma pesquisa de campo para entender qual seriam os sabores preferidos dos seus clientes. Considerando que os potenciais clientes eram os 400 estudantes matriculados e os 22 funcionários da escola, Fabrício foi até lá para realizar a sua pesquisa e obteve a seguinte resposta:
|
Sabor |
Quantidade |
|
Brigadeiro |
35 |
|
Prestígio |
40 |
|
Ninho com morango |
65 |
|
Paçoca |
48 |
|
Abacaxi com ninho |
22 |
Analisando as respostas coletadas, podemos afirmar que:
A) a pesquisa foi realizada com uma amostra de 422 pessoas.
B) a pesquisa foi realizada com uma população de 210 pessoas.
C) a pesquisa foi realizada com uma amostra de 210 pessoas.
D) a pesquisa foi realizada com uma população de 400 pessoas.
Alternativa C
A população abarca os estudantes e os funcionários, logo ela corresponde a 400 + 22 = 422 pessoas. Já a amostra é composta pelas pessoas que foram abordadas, que é igual a 35 + 40 + 65 + 48 + 22 = 210. Concluímos, então, que a pesquisa foi realizada com uma amostra de 210 pessoas.
Dados os números 10, 6, 4, 3 e 9, cinco números de uma lista de 8 números inteiros, o menor valor possível para a mediana desse conjunto é:
A) 3,0
B) 3,5
C) 4,0
D) 6,0
E) 10,0
Alternativa B
Para que mediana seja o menor valor possível, os 3 números restantes, x, y e z, devem ser menores ou iguais a 3, deixando a lista da seguinte maneira:
x, y, z, 3, 4, 6, 9, 10
Como a quantidade de termos é par, pois na sequência há 8 números, somaremos os dois termos centrais e dividiremos por 2:
(3 + 4) : 2 = 3,5
Na tabela a seguir está a média dos alunos nos 1º, 2º e 3º bimestres em Matemática.
|
Disciplina |
1º bimestre |
2º bimestre |
3º bimestre |
|
Ana |
6 |
5 |
5 |
|
Maria |
8 |
4 |
6 |
|
Pedro |
7 |
7 |
5 |
Suponha que a média da escola seja igual a 6 pontos. Se no 4º bimestre a nota de todos os estudantes for igual a 7, podemos afirmar que:
A) todos os alunos foram aprovados.
B) somente Ana foi reprovada.
C) somente Maria foi reprovada.
D) somente Pedro foi reprovado.
Alternativa B
Média de Ana:
\(\overline{X_A}=\frac{6+5+5+6}{4}=\frac{16}{4}=5,5\)
Média de Maria:
\(\overline{X_M}=\frac{8+4+6+6}{4}=\frac{24}{4}=6\)
Média de Pedro:
\(\overline{X_P}=\frac{7+7+5+6}{4}=\frac{25}{4}=6,25\ \)
Analisando as médias encontradas, concluímos que somente Ana foi reprovada.
Durante a organização das eleições para diretor escolar, os estudantes fizeram uma pesquisa sobre a intenção de voto dos alunos entre os candidatos A, B e C. Os resultados obtidos estão na tabela a seguir:
|
Candidato |
Frequência |
|
A |
120 |
|
B |
325 |
|
C |
112 |
Sabendo que na escola há 607 votantes e que as pessoas restantes não estavam na escola no dia da pesquisa, a porcentagem de pessoas não alcançadas nessa pesquisa é de aproximadamente:
A) 83,0%
B) 72,0%
C) 8,3%
D) 7,2%
E) 6,0%
Alternativa C
Primeiramente, calcularemos a quantidade de respostas obtidas:
120 + 325 + 112 = 557
Agora, calcularemos a diferença:
607 – 557 = 50
Calculando a divisão, temos que:
50 : 600 = 0,08333...
Transformando em porcentagem, temos que 0,0833... ≈ 8,3%.
O gráfico a seguir mostra a quantidade de irmãos que cada aluno do 2º ano A tinha. Os alunos que eram filhos únicos não participaram da pesquisa. Ao analisar o gráfico, o professor percebeu que os estudantes se esqueceram de colocar as porcentagens referentes a cada um dos valores.
Quantidade de irmãos dos alunos do 2º A
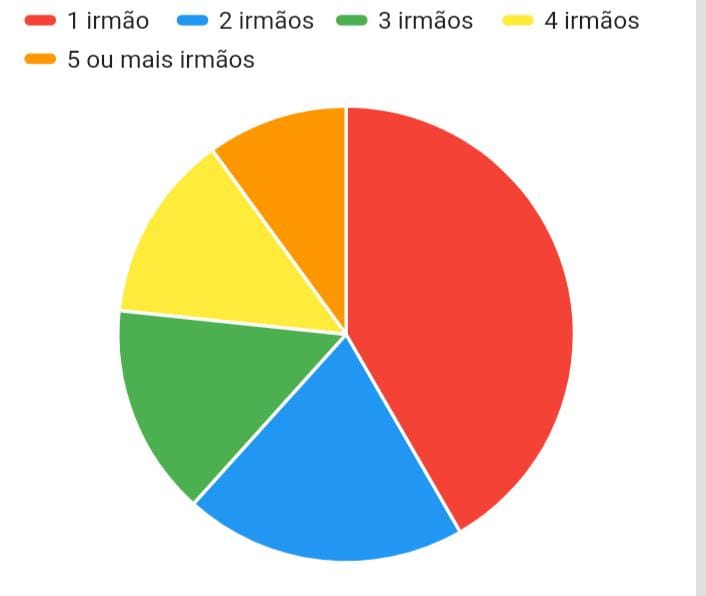
Ainda que o gráfico não tenha as porcentagens, analisando-o é possível concluir que:
A) menos da metade dos estudantes pesquisados tem 2 irmãos ou mais.
B) menos da metade dos estudantes pesquisados possui no máximo 2 irmãos.
C) a maior parte dos estudantes pesquisados possui exatamente 1 irmão.
D) mais da metade dos estudantes pesquisados tem 3 irmãos ou mais.
E) mais da metade dos estudantes pesquisados possui pelo menos 2 irmãos.
Alternativa E
Analisando os arcos, é possível concluir que mais da metade dos estudantes pesquisados possui pelo menos 2 irmãos. Note que os arcos em azul, verde, amarelo e laranja representam quem tem 2 irmãos ou mais e compreendem mais da metade do gráfico.
Durante uma pesquisa feita por um petshop, o atendente da loja realizava duas perguntas para cada um dos clientes atendidos naquele dia:
- Quais são as espécies de seus animais de estimação?
- Quantos animais de estimação de cada espécie você tem?
O resultado da pesquisa foi representado no gráfico a seguir:
Quantidade de animais dos clientes do petshop
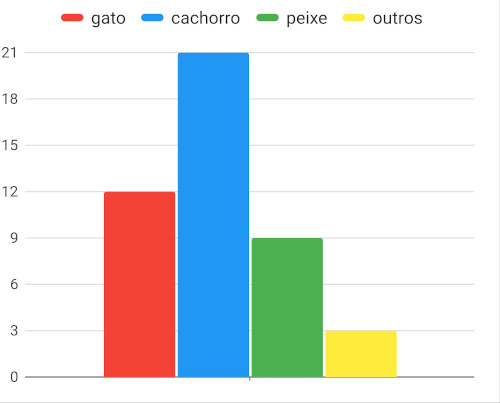
Após analisar o gráfico, julgue como verdadeira ou falsa cada uma das afirmativas a seguir:
I – Podemos inferir que a pesquisa foi respondida por 45 clientes.
II – O animal mais frequente é o cachorro, que representa aproximadamente 47% dos animais.
III – Há somente 3 animais diferentes de gato, cachorro e peixe.
Marque a alternativa correta:
A) Todas as afirmativas são verdadeiras.
B) Somente a afirmativa I é falsa
C) Somente a afirmativa II é falsa
D) Somente a afirmativa III é falsa.
Alternativa B
I – Falsa
Um mesmo cliente pode ter mais de um animal, e eles foram contabilizados.
II – Verdadeira
Quando dividimos 21 por 45, temos que:
21 : 45 = 0,47 = 47%
III – Verdadeira
Analisando o gráfico, vemos que na barra que indica “outros” há 3 animais.
Marque a alternativa que melhor define a área do conhecimento chamada estatística:
A) A estatística é a área da Matemática que estuda a probabilidade de um evento acontecer.
B) A estatística é a área da Matemática que estuda o total de combinações possíveis e o tipo de agrupamento de determinado conjunto.
C) A estatística é a área da Matemática que estuda a coleta de dados, a organização deles, suas representações em gráfico ou tabelas e suas possíveis análises.
D) A estatística é a área da Matemática que estuda o tamanho de regiões planas, desenvolvendo o cálculo de área, perímetro e volume para diferentes formas geométricas.
Alternativa C
A alternativa que melhor define a estatística é a terceira.
Os valores dos salários dos funcionários de uma empresa estão representados na tabela a seguir:
|
Cargo |
Quantidade de funcionários |
Salário |
|
Presidente |
1 |
R$ 44.500,00 |
|
Gerentes |
2 |
R$ 18.650,00 |
|
Supervisores |
4 |
R$ 9.257,80 |
|
Consultores |
80 |
R$ 3.525,00 |
|
Atendentes |
2 |
R$ 1.980,27 |
|
Auxiliar de serviços gerais |
1 |
R$ 1.212,00 |
Analisando a tabela de salários dos funcionários da empresa, podemos afirmar que:
A) a moda salarial dessa empresa é R$ 3.525,00, que é o salário dos consultores.
B) a mediana dos salários é de R$ 6.391,40.
C) a maioria dos funcionários ganha abaixo de R$ 3.525,00.
D) a moda salarial dessa empresa é o conjunto {2, 4}.
E) a média salarial dessa empresa é R$ 3.525,00.
Alternativa A
O cargo que possui a maior quantidade de funcionários é o de consultor, logo a moda será o salário de um consultor, que é de R$ 3.525,00.
