Exercícios sobre fatoração de polinômios
Durante a resolução de um problema de Matemática, o professor realizou a seguinte fatoração:
x² – 4 = (x + 2)(x – 2)
Esse caso de fatoração é conhecido como
A) trinômio quadrado perfeito.
B) diferença de dois cubos.
C) diferença de dois quadrados.
D) fatoração por agrupamento.
E) fator comum em evidência.
Alternativa C
Esse caso de fatoração de polinômio é conhecido como diferença de dois quadrados. Sabemos que podemos reescrever 4 como 2². Assim, obteremos o seguinte polinômio: x² – 2². Perceba que nesse caso existe, então, a diferença entre dois quadrados.
Simplificando o polinômio a seguir:
\(\frac{2x^3-20x^2+50x}{x^2-10x+25}\)
encontraremos
A) \(2x\)
B) \(x\ +\ 5\ \)
C) \(2(x\ –5)\)
D) \((x+5)²\)
Alternativa A
Realizando a fatoração, podemos colocar 2x em evidência no numerador. Logo, o numerador será:
\(\frac{2x\left(x^2-10x+25\right)}{x^2-10x+25}\)
Perceba que o termo \(x^2-10x+25\) aparece tanto no numerador quanto no denominador. Assim, podemos simplificar o polinômio, restando apenas 2x no numerador.
Sobre a fatoração de polinômios, marque a alternativa INCORRETA.
A) \( x²-y²=(x+y)(x –y)\)
B) \( x²+4x+4=(x+2)²\)
C) \( ax+bx+cx=x(a+b+c)\ \)
D) \( x^2-5x-25=\left(x-5\right)^2\)
E) x³ + 8 = (x + 2)(x² – 2x + 4)
Alternativa D
Dentre as alternativas, a única que não corresponde a uma fatoração de polinômio é a letra D, pois o correto seria:
\(x^2-5x+25=\left(x-5\right)^2\)
Sabendo que a + b = 8 e que a² – b² = 16, qual o valor de b?
A) 2
B) 3
C) 4
D) 5
E) 6
Alternativa B
Utilizando fatoração, sabemos que:
\(a²-b²=(a+b)(a –b)\)
Então, temos:
\((a+b)(a\ –b)=16\)
Porém, sabemos que:
\(a+b=8\)
\(8\left(a-b\right)=16\)
\(a-b=\frac{16}{8}\)
\(a-b=2\ \)
Logo, obtemos o seguinte sistema:
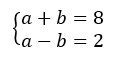
Realizando a soma das linhas:
\(2a=10\ \)
\(a=10∶2\ \)
\(a=5\)
Sabemos que a = 5, então encontraremos o valor de b:
\(a+b=8\ \)
\(5+b=8\)
\(b=8-5\ \)
\(b=3\ \)
Sabendo que x > y, a expressão algébrica
\(\frac{\left(x-y\right)\left(x^2-y^2\right)}{x+y}\)
pode ser simplificada como:
A) x + y
B) x – y
C) x² – y²
D) (x – y)²
E) (x + y)²
Alternativa D
Simplificando a expressão algébrica:
\(x^2-y^2=\left(x-y\right)\left(x+y\right)\)
Substituindo na equação:
\(\frac{\left(x-y\right)\left(x-y\right)\left(x+y\right)}{x+y}\)
Note que o termo x + y é comum ao numerador e ao denominador. Logo, podemos simplificar, restando somente:
\(\left(x-y\right)\left(x-y\right)\)
Que é o mesmo que:
\(\left(x-y\right)^2\)
O polinômio cuja fatoração é (x + y)(a + b) é:
A) x² + 2xy + 2xy + b²
B) xa + xb + yb + ya
C) xa² + yb² + xa + xb
D) ax² + 2xy + 2yb + b²
E) ax + ay – bx – bx
Alternativa B
Para encontrar o polinômio que possui fatoração igual (x + y)(a + b), basta calcularmos o produto. Aplicando a propriedade distributiva:
(x + y)(a + b) = xa + xb + ya + yb
Como a ordem das parcelas não altera a soma:
(x + y)(a + b)
xa + xb + yb + ya
Analisando as alternativas, marque aquela que corresponde à fatoração correta do seguinte polinômio:
\(x^2-10x+25\)
A) x2-52
B) x+52
C) x-52
D) x+53
E) x-53
Alternativa C
Sabemos que esse é um trinômio quadrado perfeito. Como temos -10 no termo central, ele será igual ao quadrado da diferença.
\(\sqrt x=x\)
\(\sqrt{25}=5\)
O termo central é igual a:
\(-\ 2\cdot5\cdot x=-\ 10x\ \)
Assim, temos que:
\(x^2-10x+25=\left(x-5\right)^2\)
Durante os seus estudos de Cálculo 1, Marcelo se deparou com a seguinte equação: x² + y² + 2x – 2y + 2 = 0. Realizando a fatoração, essa equação pode ser reescrita como:
A) \( (x+y)²(x –y)² \)
B) \( (x+2)²-(y+2) \)
C) \( (x\ –1)²∶(y+1)\)
D) \( (x\ –1)²+(y+1)²\)
E) \( (x+1)²+(y-1)²\)
Alternativa E
Analisando o polinômio, concluímos que podemos dividi-lo da seguinte maneira:
\((x²+2x)+(y²-2y)+2=0 \)
Sabemos que:
2 = 1 + 1
Para completar os trinômios, reescrevemos o polinômio da seguinte forma:
\(\left(x^2+2x+1\right)+\left(y^2-2x+1\right)=0\)
Realizando a fatoração:
\(\left(x+1\right)^2+\left(y-1\right)^2=0\)
(Prefeitura de Bataguassu – MS) Se ab = 8 e a²b + ab² + a + b = 90, qual o valor de a³ + b³?
A) 740
B) 750
C) 760
D) 840
Alternativa C
Fatorando a³+b³, temos:
\(a³+b³=(a+b)(a²-ab+b²) \)
Substituindo os valores conhecidos:
\(a^3+b^3=\left(a+b\right)\left(a^2-8+b^2\right)\)
Por outro lado, temos que:
\(a²b+ab²+a+b=90\)
Fatorando:
\(ab\left(a+b\right)+1\left(a+b\right)=90\)
\(8\left(a+b\right)+1\left(a+b\right)=90\)
\(9\left(a+b\right)=90\)
\(a+b=90∶9\ \)
\(a+b=10\ \)
Sabemos também que:
\(\left(a+b\right)^2={10}^2\)
\(a^2+2ab+b^2=100\)
\(a^2+b^2+2ab=100\)
Porém:
ab = 8
\(a^2+b^2+2\cdot8=100\)
\(a^2+b^2+16=100\)
\(a^2+b^2=100-16\)
\(a^2+b^2=84\)
Portanto, obtemos:
\(a^3+b^3=\left(a+b\right)\left(a^2-8+b^2\right)\)
\(a^3+b^3=10\ \left(a^2+b^2-8\right)\)
\(a^3+b^3=10\ \left(84-8\right)\)
\(a^3+b^3=10\cdot76\ \)
\(a³+b³=760 \)
(Unoesc – Prefeitura de Vargem Bonita) Com relação às expressões algébricas, são feitas as seguintes afirmações:
I. 2(4 – 2y) = 8 – 8y
II. 2(2a + 6) = 4(a + 3)
III. (x + y)² = x² + 2xy + y²
É correto o que se afirma apenas em:
A) II
B) III
C) I e III
D) II e III
Alternativa D
I. Falsa
Aplicando a propriedade distributiva, o correto seria 8 – 4y.
II. Verdadeira
Foi feita uma nova fatoração. Note que 2a e 6 são múltiplos de 2. Logo, temos que:
\(2\left(2a+6\right)=2\cdot2\left(a+3\right)=4\left(a+3\right)\)
III. Verdadeira
Esse é o quadrado da soma. Se fatorarmos x² + 2xy + y², encontraremos (x + y)².
A forma fatorada da expressão
\(\frac{3a^2+6ab+3b^2}{2a+2b+3a-3b}\)
é:
A) a + b
B) 3a + 3b
C) a – b
D) 3(a² – b²)
E) 3
Alternativa A
\(\frac{3a^2+6ab+3b^2}{3a+3b}\)
Realizando a fatoração, temos que:
\(\frac{3(a^2+2ab+b^2)}{3\ (a\ +\ b)\ }\)
\(\frac{a^2+2ab+b^2}{a\ +\ b\ }\)
\(\frac{\left(a+b\right)^2}{a+b}\)
Assim, a simplificação da expressão é:
\(a\ +\ b\)
Durante as aulas de Matemática, um estudante utilizou o seguinte método de fatoração:
\(ax+3b+bx+3a\ \)
\(ax+3a+3b+bx\ \)
\(a\left(x+3\right)+b\left(x+3\right)\)
\((a+b)(x+3)\)
Esse método de fatoração é conhecido como:
A) fator comum em evidência.
B) fatoração por agrupamento.
C) fatoração do trinômio quadrado perfeito.
D) fatoração da diferença de dois quadrados.
Alternativa B
Esse é um caso de fatoração por agrupamento, já que os termos foram agrupados de dois em dois.
A forma fatorada da expressão 27y³ – 8 é:
A) (3y – 2)³
B) (3y – 2)(3y + 2)
C) (3y + 2)(9y² – 4)
D) (3y – 2)(9y² + 6y + 4)
E) 3y (9y² – 6y + 4)
Alternativa D
Esse é um caso do cubo da diferença. Assim, temos:
\(27y³=(3y)³\)
\(8=2³ \)
\(27y^3-8=3y–23y2+2⋅3y+22\)
\(27y^3-8=\left(3y-2\right)\left(9y^2+6y+4\right)\)
