Exercícios sobre função do 1º grau
Exercícios sobre função do 1º grau são indispensáveis para que você entenda como ela pode ser aplicada em diferentes contextos do cotidiano e em diversas áreas profissionais.
Publicado por: Raul Rodrigues de OliveiraQuestões
-
Questão 1
(Enem 2018 – PPL) Uma indústria automobilística está testando um novo modelo de carro. Cinquenta litros de combustível são colocados no tanque desse carro, que é dirigido em uma pista de testes até que todo o combustível tenha sido consumido. O segmento de reta no gráfico mostra o resultado desse teste, no qual a quantidade de combustível no tanque é indicada no eixo y (vertical), e a distância percorrida pelo automóvel é indicada no eixo x (horizontal).
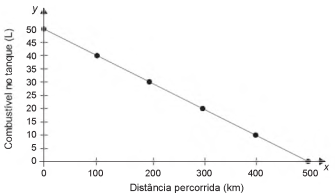
A expressão algébrica que relaciona a quantidade de combustível no tanque e a distância percorrida pelo automóvel é:
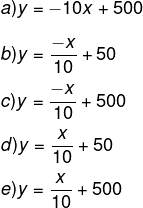
Alternativa B
Sabemos que essa situação é uma função do 1º grau, já que o gráfico é uma reta. Além disso, o ponto em que a reta toca o eixo y é o ponto (0,50).
Então, seja f(x) = ax + b:
f(0) = 50
50 = a · 0 + b
b = 50
Sendo b = 50, para encontrar o valor de a, basta encontrar outro ponto no gráfico. Usaremos o ponto (0,500):
-
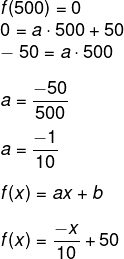
Questão 2
(Encceja 2018) Uma prestadora de serviços cobra pela visita à residência do cliente e pelo tempo necessário para realizar o serviço na residência.
O valor da visita é R$ 40 e o valor da hora para realização do serviço é R$ 20.
Uma expressão que indica o valor a ser pago (P) em função das horas (h) necessárias à execução do serviço é:
Alternativa D
A função é descrita por P = ah + b, em que b é a taxa fixa, que, no caso, é o valor da visita, que é R$ 40. Já o coeficiente a é a taxa que depende do número de horas, no caso, R$ 20. Substituindo, temos que:
P = 20h + 40
P = 40 + 20h
-
Questão 3
(Enem 2016) Uma cisterna de 6 000 L foi esvaziada em um período de 3 h. Na primeira hora foi utilizada apenas uma bomba, mas nas duas horas seguintes, a fim de reduzir o tempo de esvaziamento, outra bomba foi ligada com a primeira. O gráfico, formado por dois segmentos de reta, mostra o volume de água presente na cisterna, em função do tempo.
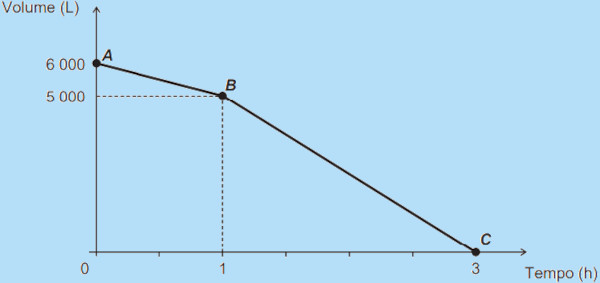
Qual é a vazão, em litro por hora, da bomba que foi ligada no início da segunda hora?
Alternativa C
No primeiro momento até a primeira hora, o volume vai de 6000 litros para 5000 litros, ou seja, ocorre uma diferença de 1000 litros, logo, a vazão da primeira bomba é de 1000 L/h. Agora, após ligar a segunda bomba, note que ela foi inteiramente esvaziada, ou seja, nas outras 2 horas, foi possível retirar 5000 L. Realizando a divisão 5000 : 2 = 2500, a soma das vazões das bombas foi de 2500 L/h.
Sabemos que a primeira bomba tem vazão de 1000 L/h, então, para descobrir a vazão da segunda, temos que: 2500 – 1000 = 1500 L.
-
Questão 4
(UFSM) Sabe-se que o preço a ser pago por uma corrida de táxi inclui uma parcela fixa, que é denominada bandeirada, e uma parcela variável, que é função da distância percorrida. Se o preço da bandeirada é de R$ 4,60 e o quilômetro rodado é R$ 0,96, a distância percorrida pelo passageiro que pagou R$ 19 para ir de sua casa ao shopping é de:
Alternativa C
Seja d a distância percorrida em quilômetros, sabemos que:
19 = 0,96d + 4,6
Isolando a incógnita, temos que:
19 – 4,6 = 0,96d
14,4 = 0,96d
d = 14,4 : 0,96
d = 15
-
Questão 5
Uma determinada espécie de pimenta, ao atingir 20 centímetros de altura, começa a crescer de forma linear. A cada dia que se passa, essa planta aumenta 2,5 centímetros. Assim, é possível descrever essa situação como uma função do 1º grau, em que a altura h(d) está em função dos dias, cuja lei de formação é:
Alternativa B
Seja h(d) = ad + b uma função afim, sabemos que b é a taxa fixa, no caso, 20 cm, e que, além disso, a cada dia, ela aumenta 2,5 cm, ou seja, 2,5 d. Dessa forma, a lei de formação que melhor descreve essa situação é:
h(d) = 2,5d + 20
-
Questão 6
Um fazendeiro resolveu investir em uma colheitadeira para facilitar o serviço na plantação. Sabendo que o valor pago foi de R$ 300.000 no ano da compra, é bastante comum que máquinas desse porte percam o seu valor V ao decorrer dos anos t. Supondo que a taxa de depreciação de uma máquina desse porte é de R$ 22.000 por ano, devido ao seu constante uso, podemos afirmar que o valor da colheitadeira, ao final de 7 anos, será de:
Alternativa C
A função que descreve o valor em função do tempo possui a lei de formação:
V(t) = -22.000t + 300.000
Como o tempo foi de 7 anos, então faremos t = 7.
V(7) = -22.000 · 7 + 300.000
V(7) = -154.000 + 300.000
V(7) = 146.000
-
Questão 7
O uso de aplicativos para realizar viagens é cada vez mais comum no cotidiano. Supõe-se que, para calcular o valor da viagem em um aplicativo, há um valor fixo mais um total de R$ 1,40 por quilômetros rodado. Sabendo que um cliente pagou R$ 15,60 ao final da viagem, a quantidade de quilômetros rodados foi de 8 km, então o valor fixo da viagem foi de:
Alternativa D
Sabemos que o valor pago é calculado por:
V(q) = 1,40q + T
Sendo T a taxa fixa e q os quilômetros rodados, substituindo os valores conhecidos, temos:
15,60 = 1,40 · 8 + T
15,60 = 11,20 + T
15,60 – 11,20 = T
T = 4,40
-
Questão 8
Dada a função afim f(x) = ax + b, sabendo-se que f(3) = 6 e f (-2) = -3, o valor do coeficiente angular dessa função é:
Alternativa A
Sabemos que f(x) = ax + b.
Substituindo os valores conhecidos, temos que:
f(3) = 6
f(3) = 3a + b → 3a + b = 6
f(-2) = -3
f(-2) = -2a + b → -2a + b = -3
Dessa foma, vamos resolver o sistema de equação:
3a + b = 6
-2a + b = -3
Realizando a subtração do primeiro pelo segundo sistema, temos que:
5a = 9
a = 9/5
-
Questão 9
Podemos afirmar que o zero da função f(x) = -2x + 5 é igual a:
Alternativa B
Para encontrar o zero da função, vamos igualar a função a zero e resolver a equação, então, temos que:
-2x + 5 = 0
-2x = -5
x = (-5) : (-2)
x = 2,5
-
Questão 10
Seja f(x) e g(x), funções cujas leis de formação são, respectivamente, f(x) = 2x -5 e g(x) = -x + 2, podemos afirmar que o valor de f(g(2)) – g(-3) é igual a:
Alternativa D
Sabendo que:
f(x) = 2x -5 e que g(x) = -x + 2, vamos calcular o valor da expressão: f(g(2)) – g(-3). Para isso calcularemos os valores separados.
Primeiro g(2):
g(2) = -2 + 2 = 0
Então, f(g(2)) = f(0):
f(g(2)) = f(0) = 2 · 0 – 5 = -5
Por fim, vamos calcular o valor de g(-3):
g(-3) = - (-3) + 2 = 3 + 2 = 5
Sendo assim, temos que:
f(g(2)) – g(-3) = -5 – 5 = -10
-
Questão 11
Julgue as afirmativas a seguir sobre a função f(x) = 2x – 3. Podemos afirmar que:
I – O coeficiente angular é 2.
II – O coeficiente linear é 3.
III – A imagem da função para x = 1 é -1.
De acordo com o julgamento das afirmativas, é correto afirmar que:
Alternativa D
I → Verdadeira, pois o coeficiente angular é o termo que acompanha a incógnita x, que, no caso, é igual a 2.
II → Falsa, pois o coeficiente linear é o termo independente, que, nesse caso, é -3.
III → Verdadeira, pois f(1) = 2 · 1 – 3 = 2 – 3 = -1.
Então, podemos concluir que I e III são verdadeiras e que II é falsa.
-
Questão 12
Sobre o comportamento da função f(x) = 4x – 3, marque a alternativa correta:
Alternativa A
Para saber se a função é crescente ou decrescente, basta olhar o coeficiente angular. Se ele for positivo, a função é crescente, se for negativo, ela será decrescente. Nesse caso a = 4, então, a função é crescente, pois seu coeficiente angular é positivo e igual a 4.