Exercícios sobre função composta
Exercícios sobre função composta, que pega elementos do domínio da função f(x) e leva ao contradomínio de g(x). A função composta é uma função aplicada em outra função.
Publicado por: Raul Rodrigues de OliveiraQuestões
-
Questão 1
Dada as funções de lei de formação f(x) = 2x + 5 e g(x) = -3x + 1, podemos afirmar que o valor de f (g(1)) é igual a:
Alternativa D
Primeiro calcularemos g(1):
g(x) = -3x + 1
g(1) = -3 · 1 + 1
g(1) = -3 + 1
g(1) = -2
Agora que conhecemos o valor de g(1), calcularemos f(g(1)), ou seja, f(-2):
f(x) = 2x + 5
f(-2) = 2 · (-2) + 5
f(-2) = -4 + 5
f(-2) = 1
-
Questão 2
Conhecendo as funções f(x) log2x + 1 e a função g(x) = 2x, então, a função f(g(x)) é dada pela lei de formação:
Alternativa C
Na função f(x) = log2x, vamos substituir sua incógnita pela função g(x) = 2x. Então, temos que:
f(g(x)) = log22x + 1
f(g(x)) = x log22 + 1
f(g(x)) = x · 1 + 1
f(g(x)) = x + 1
-
Questão 3
Dada a função f(x) = x + 3 e a função g(x) = 2x – 5, o zero da função f(g(x)) é:
Alternativa B
Primeiro encontraremos f(g(x)):
f(g(x)) = (2x – 5) + 3
f(g(x)) = 2x – 5 + 3
f(g(x)) = 2x – 2
Para encontrar o zero da função, vamos igualar a função a zero, ou seja:
-
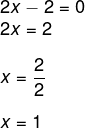
Questão 4
(Acafe - SC) Dadas as funções reais f(x) = 2x – 6 e g(x) = ax + b, se f[g(x)] = 12x + 8, o valor de a + b é:
Alternativa B
Sendo f(x) = 2x – 6; g(x) ax + b; e f[g(x)] = 12x + 8, então, temos que:
f[g(x)] = 2 (ax + b) – 6
12x + 8 = 2ax + 2b – 6
Igualando os termos para encontrar o valor de a, temos que:
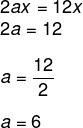
Encontrando o valor de b:
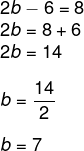
Por fim, o valor de a + b:
6 + 7 = 13
-
Questão 5
Dadas as funções f(x) = √x e g(x) = x² – 2x + 1, então, o valor de (g o f)(9) é:
Alternativa E
Primeiro calcularemos f(9):
f(x) = √x
f(9) = √9
f(9) = 3
Então, (g o f)(9) = g(3):
g(x) = x² – 2x + 1
g(3) = 3² – 2 · 3 + 1
g(3) = 9 – 6 + 1
g(3) = 3 + 1
g(3) = 4
-
Questão 6
(UPF) Um estudo das condições ambientais de um município do Rio Grande do Sul indica que a taxa média de monóxido de carbono (CO) no ar será de C(P) = 0,2P – 1 partes por milhão (ppm) quando a população for P milhares de habitantes. Sabe-se que, em t anos, a população desse município será dada pela relação 2 P(t) = 50 + 0,05t2. O nível de monóxido de carbono, em função do tempo t, é dado por:
Alternativa A
Para encontrar a função, temos que:
C(P) = 0,2 P – 1, substituindo P por 50 + 0,05t2, temos que:
C(t) = 0,2 (50 + 0,05t2 ) – 1
C(t) = 10 + 0,01t2 – 1
C(t) = 9 + 0,01 t2
-
Questão 7
Uma loja de roupas recebe um lucro de 30% em cima da venda de qualquer peça, ou seja, a função lucro é: L(x) = 0,3x, em que x é o valor do produto. Dado o valor do produto, a fábrica o vende pelo dobro do valor gasto mais um adicional de R$ 10, ou seja, V(g) = 2g + 10, em que g é o valor gasto para produzi-lo. A função que dá o lucro em função do valor do gasto g é:
Alternativa B
Temos que L(x) = 0,3x. Na função lucro, vamos substituir x por 2g + 10, então, temos que:
L(g) = 0,3 (2g + 10)
L(g) = 0,6g + 3
-
Questão 8
(Unicamp 2020) Sabendo que ? é um número real, considere a função f(x) = ax + 2 definida para todo número real ?. Se f(f(1)) = 1, então:
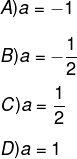
Alternativa A
Analisando a função, temos que:
f(f(1)) = 1
Sabemos que:
f(1) = a · 1 + 2
f(1) = a + 2
Então:
f(f(1)) = f(a + 2)
f(a + 2) = 1
a(a + 2) + 2 = 1
a² + 2a + 2 = 1
a² + 2a + 2 – 1 = 0
a² + 2a + 1 = 0
Fatorando esse polinômio, que é um produto notável, temos que:
a² + 2a + 1 é um binômio quadrado perfeito, podemos reescrevê-lo como (a + 1)², sendo assim:
(a + 1)² = 0
a + 1 = 0
a = -1
-
Questão 9
(FGV) Considere as funções f(x) = 2x + 1 e g(x) = x² – 1. Então, as raízes da equação f(g(x)) = 0 são:
Alternativa E
Na função f(x) = 2x + 1, vamos substituir o x por x² – 1:
f(g(x)) = 2(x² – 1) + 1
f(g(x)) = 2x² – 2 + 1
f(g(x)) = 2x² – 1
Queremos igualar essa função a zero:
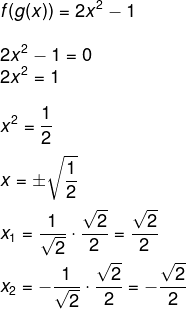
Desse modo, as raízes são opostas.
-
Questão 10
Dada a função f(x) = 2x + 1 e g(x) = x – 1, julgue as sentenças a seguir:
I → (f o g)(x) = (g o f)(x)
II → (g o f)(2) = 4
III → (f o g)(1) = 1
As afirmativas são, respectivamente:
Alternativa B
I → (f o g)(x) = (g o f)(x) — falsa
Primeiro encontraremos (f o g)(x):
(f o g)(x) = 2(x – 1) + 1
(f o g)(x) = 2x – 2 + 1
(f o g)(x) = 2x – 1
Agora vamos encontrar (g o f)(x):
(g o f)(x) = (2x + 1) – 1
(g o f)(x) = 2x + 1 – 1
(g o f)(x) = 2x
II → (g o f)(2) = 4 — verdadeira
(g o f)(x) = 2x
(g o f)(2) = 2 · 2
(g o f)(x) = 4
III → (f o g)(1) = 1 — verdadeira
(f o g)(x) = 2x – 1
(f o g)(1) = 2 · 1 – 1
(f o g)(1) = 2 – 1
(f o g)(1) = 1
A sequência correta é F, V e V.
-
Questão 11
(Mackenzie - SP) As funções f(x) = 3 – 4x e g(x) = 3x + m são tais que f(g(x)) = g(f(x)), qualquer que seja x real. O valor de m é:
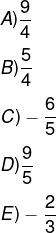
Alternativa C
Primeiro encontraremos f(g(x)):
f(g(x)) = f(x) = 3 – 4 (3x + m)
f(g(x)) = 3 – 12x – 4m
f(g(x)) = -12x – 4m + 3
Agora encontraremos g(f(x)):
g(f(x)) = 3 (3 – 4x) + m
g(f(x)) = 9 – 12x + m
g(f(x)) = -12x + m + 9
Por fim, vamos igualar as duas leis de formação:
-12x – 4m + 3 = -12x + m + 9
-12x + 12x – 4m – m = 9 – 3
-5m = 6 · (-1)
5m = -6
m = -6/5
Então, temos que
-
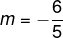
Questão 12
Dada a função f(x) = -20x + 15 e g(x) = 15x – 6, julgue as sentenças a seguir:
I → f(g(x)) = g(f(x))
II → f(g(0)) = -6
III → g(f(0)) = 219
As afirmativas são, respectivamente:
Alternativa C
I → f(g(x)) = g(f(x)) — falsa
Primeiro vamos encontrar a lei de formação da função f(g(x)):
f(g(x)) = -20 (15x – 6) + 15
f(g(x)) = -300x + 120 + 15
f(g(x)) = -300x + 135
Agora g(f(x)):
g(f(x)) = 15 (-20x + 15) – 6
g(f(x)) = -300x + 225 – 6
g(f(x)) = -300x + 219
II → f(g(0)) = -6 — falsa
f(g(x)) = -300x + 135
f(g(0)) = -300 · 0 + 135
f(g(0)) = 135
III → g(f(0)) = 219 — verdadeira
g(f(x)) = -300x + 219
g(f(0)) = -300 · 0 + 219
g(f(0)) = 219
A sequência correta é F, F e V.