Exercícios sobre função definida por fórmula
Se A = {0, 1, 2, 3, 4} e B = {– 4, – 3, – 2, – 1, 0, 1, 2}, verifique se as expressões a seguir caracterizam funções em que A é o domínio e B é o contradomínio da função:
a) f(x) = – x
b) f(x) = – x + 1
c) f(x) = x² – x
a) Para verificar se a fórmula f(x) = – x define uma lei de função de A → B, faremos uma tabela para verificar a imagem obtida pelos elementos de A:
|
x |
f(x) = – x |
|
0 |
f(x) = – x = 0 |
|
1 |
f(x) = – x = – 1 |
|
2 |
f(x) = – x = – 2 |
|
3 |
f(x) = – x = – 3 |
|
4 |
f(x) = – x = – 4 |
Nesse caso, a expressão f(x) = – x define uma função de A → B.
b) Vejamos agora se f(x) = – x + 1 define uma lei de função de A → B. Montando novamente uma tabela, verificaremos a imagem obtida pelos elementos de x pertencentes ao conjunto A:
|
x |
f(x) = – x + 1 |
|
0 |
f(x) = – x + 1 = 0 + 1 = 1 |
|
1 |
f(x) = – x + 1 = – 1 + 1 = 0 |
|
2 |
f(x) = – x + 1 = – 2 + 1 = – 1 |
|
3 |
f(x) = – x + 1 = – 3 + 1 = – 2 |
|
4 |
f(x) = – x + 1 = – 4 + 1 = – 3 |
Como todos os elementos de A possuem um único correspondente em B, então f(x) = – x + 1 caracteriza uma função de A → B.
c) Através de uma tabela, vamos verificar se a fórmula f(x) = – x define uma lei de formação da função de A → B:
|
x |
f(x) = x² – x |
|
0 |
f(x) = x² – x = 0 – 0 = 0 |
|
1 |
f(x) = x² – x = 1² – 1 = 0 |
|
2 |
f(x) = x² – x = 2² – 2 = 2 |
|
3 |
f(x) = x² – x = 3² – 3 = 6 |
|
4 |
f(x) = x² – x = 4² – 4 = 12 |
Nesse caso, a expressão f(x) = x² – x não define uma função de A → B, pois os elementos x = 3 e x = 4 não possuem imagem em B.
Considere f uma função com domínio nos reais de forma que sua lei de formação seja dada por f(x) = – x² + 2x – 3. Sendo assim, determine:
a) f(0)
b) f(1)
c) f(-1)
d) o valor de x para o qual tenhamos f(x) = 0.
a) Para encontrar o valor de f(0), onde houver x, substituiremos por 0 na função f(x) = x² + 2x – 3:
f(x) = – x² + 2x – 3
f(0) = – 0² + 2.0 – 3
f(0) = – 3
Portanto, f(0) = – 3.
b) Novamente, vamos substituir x por 1 na função f(x) = – x² + 2x – 3:
f(x) = – x² + 2x – 3
f(1) = – 1² + 2.1 – 3
f(1) = – 1 + 2 – 3
f(1) = – 2
Portanto, f(1) = – 2.
c) Vamos agora substituir x por – 1 em f(x) = – x² + 2x – 3:
f(x) = – x² + 2x – 3
f(– 1) = – (– 1)² + 2.(– 1) – 3
f(– 1) = – 1 – 2 – 3
f(– 1) = – 6
Portanto, f(1) = – 6.
d) Agora em vez de substituirmos o x, substituiremos f(x) por 0 para determinar o valor de x:
f(x) = – x² + 2x – 3
0 = – x² + 2x – 3
x² – 2x + 3 = 0
Para resolver, é preciso aplicar a Fórmula de Bhaskara:
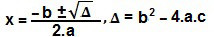
Δ = (– 2)² – 4.1.3
Δ = 4 – 12
Δ = – 8
Como Δ < 0 e f está definido nos reais, então não existe valor de x, tal que f(x) = 0, no conjunto dos reais.
(FGV-SP) O preço de ingresso numa peça de teatro (p) relaciona-se com a quantidade de frequentadores (x) por sessão através da relação p = – 0,2x + 100.
a) Qual a receita arrecadada por sessão, se o preço de ingresso for R$ 60,00?
b) Qual o preço que deve ser cobrado para dar a máxima receita por sessão?
Observação: receita = preço · quantidade
a) Se p representa o preço dos ingressos e sabemos que em determinada sessão esse valor foi de R$ 60,00, então basta substituirmos p por 60 em p = – 0,2x + 100:
p = – 0,2x + 100
60 = – 0,2x + 100
0,2x = 100 – 60
0,2x = 40
x = 40
0,2
x = 200
Se x = 200, a quantidade de frequentadores foi de 200. Precisamos agora determinar o valor da receita. Para isso, faremos:
receita = preço · quantidade
receita = 60 · 200
receita = 12000
Então, com o ingresso no valor de R$60,00, a receita arrecadada por sessão é de R$ 12.000,00.
b) Se R é a receita arrecadada por sessão, p é o preço dado por p = – 0,2x + 100 e x é a quantidade de frequentadores, pela fórmula do cálculo da receita, temos:
receita = preço · quantidade
R = p · x
R = (– 0,2x + 100) · x
R = – 0,2x² + 100x
Temos aqui uma função do segundo grau. Para determinar o valor referente à máxima receita, utilizaremos o cálculo do vértice da parábola, isto é:
xv = – b = – 100 = 250
2a – 0,4
Portanto, a quantidade de frequentadores deve ser de x = 250. Substituindo esse valor na relação p = – 0,2x + 100, teremos:
p = – 0,2x + 100
p = – 0,2 · 250 + 100
p = – 50 + 100
p = 50
Então, para obter a máxima receita por sessão, o preço do ingresso deve ser R$ 50,00.
(UFPI) A tabela a seguir mostra alguns valores de uma função y = f(x).
|
x |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
|
y |
– 1 |
0 |
3 |
8 |
15 |
24 |
35 |
Essa função é definida pela expressão:
a) f(x) = x² – 1
b) f(x) = x² + 1
c) f(x) = – x² – 1
d) f(x) = – x² + 1
e) f(x) = 2x² – 1
A função y = f(x) é do segundo grau, portanto, é do tipo f(x) = ax² + bx + c. Para determinar a lei da função f(x), devemos analisar três relações estabelecidas pela tabela: f(0) = – 1, f(1) = 0 e f(2) = 3. A partir da primeira relação, temos:
ax² + bx + c = f(x)
a.0² + b.0 + c = – 1
c = – 1
Já encontramos o valor de c, agora, a partir da segunda relação, temos:
ax² + bx + c = f(x)
a.1² + b.1 – 1 = 0
a + b = 1
E da terceira relação segue:
ax² + bx + c = f(x)
a.2² + b.2 – 1 = 3
4a + 2b = 4
2a + b = 2
Podemos montar um sistema de equações entre as duas últimas igualdades encontradas:
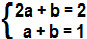
Substituindo a segunda equação na primeira, temos:
(2a – a) + (b – b) = (2 – 1)
a + 0 = 1
a = 1
Substituindo o valor encontrado de a em a + b = 1, temos:
a + b = 1
1 + b = 1
b = 0
Substituindo os valores encontrados de a, b e c em f(x) = ax² + bx + c, temos:
f(x) = ax² + bx + c
f(x) = 1x² + 0x + (– 1)
f(x) = x² – 1
Portanto, a alternativa correta é a letra a.
