Exercícios sobre função injetora
Dada a função \(\mathbb{R}\rightarrow\mathbb{R}\) com lei de formação \(f\left(x\right)=2x+1\), podemos afirmar que essa função é:
A) uma função do 2º grau.
B) uma função linear.
C) uma função constante.
D) uma função injetora.
E) uma função exponencial.
Alternativa D
Como essa é uma função do primeiro grau, sabemos que valores distintos de x possuem imagens distintas. Vale ressaltar que o gráfico de uma função do primeiro grau é uma reta, logo elementos distintos de x possuem imagens distintas em y.
Há uma função f: A →B que descreve o ganho de uma indústria em função da quantidade de peças produzidas e traduz a lei de oferta e demanda para aquele produto. O conjunto A é o total de peças produzidas no mês, e o conjunto B é o lucro obtido com aquela produção. Existem dois casos distintos para o ganho de R$ 10.000,00: quando são produzidas 20.000 peças e quando são produzidas 45.000. Analisando essa função, podemos afirmar que:
A) essa função é injetora, pois f (45.000) = 10.000,00 e f (20.000) = 10.0000.
B) essa função é injetora, pois o domínio é o conjunto dos números naturais.
C) essa função não é injetora, porque dois valores distintos possuem a mesma imagem.
D) essa função não é injetora, porque o contradomínio é o conjunto dos números reais positivos.
Alternativa C
Podemos afirmar que essa função não é injetora, pois f (45.000) = f (20.000) = 10.000,00, ou seja, elementos distintos do domínio possuem a mesma imagem no contradomínio.
Existem várias classificações para funções, sendo uma delas a de função injetora. Uma função é dita injetora se:
A) para todo elemento do domínio a imagem é sempre a mesma.
B) para dois elementos distintos do domínio, as imagens também são distintas.
C) todo elemento do domínio possui um único correspondente no contradomínio.
D) todo elemento do contradomínio é correspondente de pelo menos um elemento no domínio.
Alternativa B
Uma função é injetora se dois elementos diferentes do domínio possuem imagens diferentes no contradomínio.
Sendo f: A → B uma função cuja lei de formação é f (x,y) = x ⋅ y com conjunto A = {(0,1)(0,2),(1,2),(1,3),(2,3)} e contradomínio B = {0, 1, 2, 3, 6}, julgue as afirmativas a seguir como verdadeira (V) ou falsa (F):
I. f (0,1) = f (0,2)
II. Essa função é injetora.
III. Essa função é polinomial do 1º grau.
A) VVV
B) VFV
C) FFV
D) FVF
E) VFF
Alternativa E
I. Verdadeira
f (0,1) = 0 ⋅ 1 = 0
f (0,2) = 0 ⋅ 2 = 0
f (0,1) = f (0,2)
II. Falsa
Como há dois elementos distintos no domínio que possuem a mesma imagem, pois f (0,1) = f (0,2), essa função não é injetora.
III. Falsa
A função afim deve possuir lei de formação f(x) = ax + b, logo a função do enunciado não pode ser classificada como tal.
Durante a aula de Matemática, o professor fez o desenho do diagrama a seguir e pediu para que cada aluno formasse uma frase sobre a relação entre os conjuntos A e B:
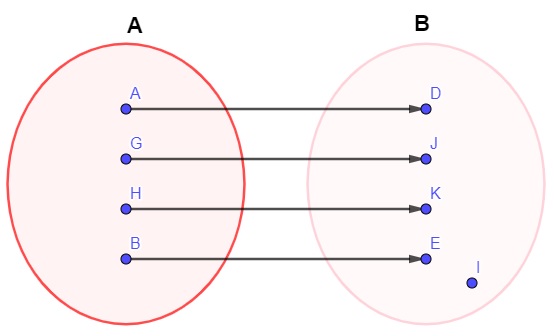
Ana: Essa relação não descreve uma função, pois há elementos do conjunto B que não são correspondentes de nenhum elemento do conjunto A.
Beatriz: Essa relação é uma função, pois todo elemento do conjunto A possui um número correspondente no conjunto B.
Camila: Essa relação é uma função injetora, pois elementos distintos do conjunto A possuem imagens distintas no conjunto B.
Marque a alternativa correta:
A) A afirmativa de Ana está incorreta, e as afirmativas de Beatriz e Camila estão corretas.
B) A afirmativa de Ana está correta, e as afirmativas de Beatriz e Camila estão incorretas.
C) A afirmativa de Beatriz está correta, e as afirmativas de Ana e Camila estão incorretas.
D) As afirmativas de Ana, Beatriz e Camila estão corretas.
E) As afirmativas de Ana, Beatriz e Camila estão incorretas.
Alternativa A
Afirmativa de Ana: falsa
A afirmativa de Ana Está incorreta, pois ainda que haja elementos no conjunto B que não são correspondentes de nenhum elemento no conjunto A, a relação entre A e B é uma função, pois todo elemento de A possui um único correspondente em B.
Afirmativa de Beatriz: verdadeira
A relação é, de fato, uma função.
Afirmativa de Camila: verdadeira
Essa função é, de fato, injetora.
A seguir, foram representadas duas funções distintas no plano cartesiano, a função 1 e a função 2:
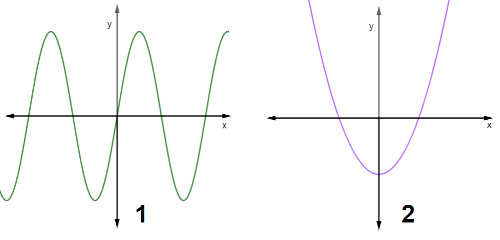
Analisando o gráfico, podemos afirmar que:
A) Somente a função 1 é injetora.
B) Somente a função 2 é injetora.
C) A função 1 e a função 2 são injetoras.
D) A função 1 e a função 2 não são injetoras.
Alternativa D
Nenhuma das funções é injetora, pois se traçarmos uma reta paralela ao eixo x, em determinados pontos do gráfico será possível perceber que existem valores distintos no domínio que possuem a mesma imagem, ou seja, valores diferentes de x são correspondentes a um mesmo valor y.
Analise os gráficos 1 e 2 a seguir:
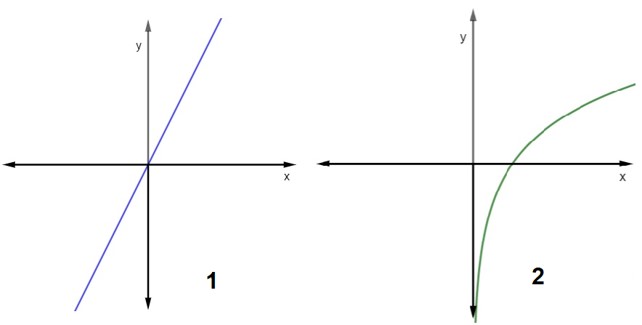
Analisando as imagens, podemos afirmar que:
A) somente o gráfico 1 representa uma função injetora.
B) somente o gráfico 2 representa uma função injetora.
C) ambos os gráficos representam funções injetoras.
D) nenhum dos gráficos representa funções injetoras.
Alternativa C
Podemos perceber que, nos dois casos, para um valor de x existe sempre um único correspondente em y. Logo, nesse intervalo, elementos distintos do domínio possuem também imagens distintas, o que faz com que ambos os gráficos representem funções injetoras.
A função f : A → B, com lei de formação f (x) = 2x², sendo A = {0, 1, 2,3} e B = {0, 1, 2, 8, 18}, pode ser classificada como:
A) injetora
B) sobrejetora
C) bijetora
D) exponencial
Alternativa A
Analisando a função, temos que:
\(f\left(0\right)=2\cdot0^2=2\cdot0=0\)
\(f\left(1\right)=2\cdot1^2=2\cdot1=2\)
\(f\left(2\right)=2\cdot2^2=2\cdot4=8\)
\(f\left(3\right)=2\cdot3^2=2\cdot9=18\)
Podemos afirmar que essa função é injetora, pois elementos distintos do domínio possuem imagens distintas no contradomínio.
Note que não há nenhum valor do domínio que faz com que f(a) = 1, logo o elemento 1 que pertence ao contradomínio não é imagem de nenhum elemento, portanto essa não é uma função sobrejetora. Como ela não é sobrejetora, ela não pode ser uma função bijetora, pois a função é bijetora se for injetora e sobrejetora. Concluímos, assim, que essa função é injetora.
Analise as funções a seguir:
I. \(f:\ \mathbb{R}\ \rightarrow\mathbb{R}\ |\ f(x)\ =\ -\ 2x\)
II. \(f:\ \mathbb{R}\ \rightarrow\mathbb{R}\ |\ f(x)\ =\ -\ 2x²\)
III. \(\ f:\ \mathbb{R}\ \rightarrow\mathbb{R}\ |\ f\left(x\right)=2^x\)
Podemos classificar como função(ões) injetora(s):
A) somente a alternativa I.
B) somente a alternativa II.
C) somente a alternativa III.
D) somente as alternativas I e III.
E) todas as alternativas.
Alternativa D
I. É injetora
A função afim possui como gráfico uma reta. Por meio dela, sabemos que elementos distintos possuem sempre imagens distintas, então I é uma função injetora.
II. Não é injetora
Na função quadrática, dado um valor a pertencente ao domínio e o seu oposto -a, pelo fato de a² ser igual a (-a)², temos que f(a) = f(-a).
III. É injetora
A função exponencial é injetora, pois dados elementos diferentes do domínio, a imagem também será diferente.
Na imagem a seguir há um diagrama que demonstra uma relação f entre o conjunto A e o conjunto B.
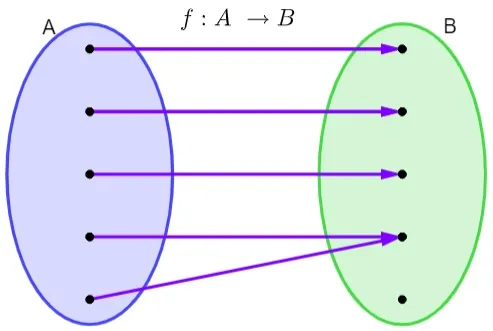
Analisando essa imagem, podemos afirmar que:
A) essa relação não descreve uma função, pois existe um elemento sobrando no conjunto B.
B) essa relação não descreve uma função, pois existem dois elementos no conjunto A com o mesmo correspondente no conjunto B.
C) essa relação é uma função injetora, pois existem dois elementos distintos do conjunto A com o mesmo correspondente no conjunto B.
D) essa relação é uma função, mas não é injetora, pois existem dois elementos distintos do conjunto A com o mesmo correspondente no conjunto B.
Alternativa D
Todos os elementos de A possuem um único correspondente em B, logo essa relação é uma função. Entretanto, há elementos distintos do conjunto A que possuem o mesmo correspondente no conjunto B, portanto não se trata de uma função injetora, pois existem dois elementos no conjunto A com o mesmo correspondente no conjunto B.
(ESA) Com relação às funções injetoras, sobrejetoras e bijetoras, podemos afirmar que:
A) Se é injetora e não é sobrejetora, então ela é bijetora.
B) Se é sobrejetora, então ela é injetora.
C) Se é injetora e sobrejetora, então ela é bijetora.
D) Se é injetora, então ela é sobrejetora.
E) Se é sobrejetora e não é injetora, então ela é bijetora.
Alternativa C
Uma função é conhecida como bijetora se ela for injetora e sobrejetora ao mesmo tempo.
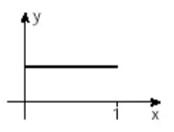
(Unifesp) Há funções y = f(x) que possuem a seguinte propriedade: “a valores distintos de x correspondem valores distintos de y”. Tais funções são chamadas injetoras. Qual, dentre as funções cujos gráficos aparecem abaixo, é injetora?
A) 
B) 
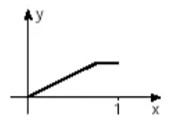
C) 
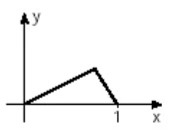
D) 
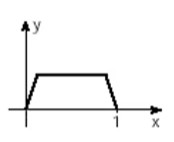
E) 
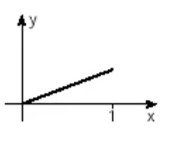
Alternativa E
O único gráfico que demonstra que dois elementos distintos do domínio possuem também imagens distintas é o gráfico da alternativa E.
Podemos observar que nas alternativas A, B e D existe um momento em que a função é constante em parte, ou seja, para valores diferentes de x, o y possui o mesmo valor. Já no gráfico da função C, podemos perceber que ele atinge o seu máximo e posteriormente volta assumir os valores de y que foram assumidos anteriormente, logo esse gráfico não descreve uma função injetora.
