Home
Exercícios de Matemática
Exercícios sobre função logarítmica

Exercícios sobre função logarítmica

Esta lista de exercícios testará seus conhecimentos sobre a função logarítmica, que é a função que possui em sua lei de formação o logaritmo de uma variável. Publicado por: Raul Rodrigues de Oliveira

Imprimir

Questão 1

Dada a função $f\left(x\right)=log_3x$ , o valor da expressão $f\left(9\right)-f\left(81\right)$ é igual a:

A) 3

B) 2

C) -1

D) -2

E) -3

Ver resposta

Resposta

Alternativa D

Calculando, temos:

$f\left(9\right)-f\left(81\right)=log_39-log_381$

$f\left(9\right)-f\left(81\right)=2-4$

$f\left(9\right)-f\left(81\right)=-2$

Questão 2

O crescimento de uma determinada cultura de bactérias pode ser descrito por uma função logarítmica, com lei de formação $f\left(x\right)=2+log_2\left(x+4\right)$ , em que x é o tempo em anos e $f\left(x\right)$ é a quantidade de bactérias em milhares.

Nessas condições, a quantidade de bactérias que existirá após 5 anos é igual a:

A) 5

B) 4

C) 3

D) 2

E) 1

Ver resposta

Resposta

Alternativa B

Queremos que $f\left(x\right)=2+log_2\left(x+4\right)$

$2+log_2\left(x+4\right)=5$

$log_2\left(x+4\right)=5-2$

$\ log_2\left(x+4\right)=3$

Aplicando a definição de log:

$2^3=x+4$

$8=x+4$

$8-4\ =x$

$x=4\$

Questão 3

Sobre a função logarítmica, é correto afirmar que:

I – A função logarítmica é sempre crescente.

II – A lei de formação da função logarítmica é $f\left(x\right)=log_ax$ .

III – A função logarítmica é a função inversa da função exponencial.

Podemos afirmar que:

A) Somente a afirmativa I é falsa.

B) Somente a afirmativa II é falsa.

C) Somente a afirmativa III é falsa.

D) Todas as afirmativas são verdadeiras.

Ver resposta

Resposta

Alternativa A

I – Falsa

A função logarítmica pode ser crescente ou decrescente.

II – Verdadeira

A lei de formação da função logarítmica possui a variável no logaritmando.

III – Verdadeira

De fato, a função logarítmica é a função inversa da função exponencial.

Questão 4

Uma função logarítmica possui lei de formação igual a $f\left(x\right)=log_2x$ . Qual deve ser o valor de x para que $f\left(x\right)=10$ ?

A) 64

B) 128

C) 256

D) 512

E) 1024

Ver resposta

Resposta

Alternativa E

Queremos que $f\left(x\right)=log_2x=10$

Aplicando a definição de logaritmo:

$2^{10}=x$

$x=1024\$

Questão 5

Uma função logarítmica é considerada decrescente quando:

A) o valor da base do logaritmo é um número negativo.

B) o valor da base do logaritmo é uma fração.

C) o valor da base do logaritmo é um número positivo.

D) o valor da base do logaritmo é um número menor que 1.

E) o valor da base do logaritmo é igual a 1.

Ver resposta

Resposta

Alternativa D

Para que a função logarítmica tenha comportamento decrescente, é necessário que a sua base seja um número menor que 1. Vale ressaltar que a base do logaritmo, por definição, não é um número negativo.

Questão 6

Estudos do IBGE constataram que o tempo de vida de uma população pode ser descrita pela função $T(x)=16\cdot(250\ log\ x-844),$ em que x é igual a um determinado ano. Caso esse comportamento seja mantido durante muitos anos, a expectativa de vida para essa população nos anos 3000 será de: (Use log3 = 0,4)

A) 67 anos

B) 78 anos

C) 84 anos

D) 96 anos

E)100 anos

Ver resposta

Resposta

Alternativa D

Calculando o valor da função para x = 3000:

$T\left(x\right)=16\cdot\left(250logx-844\right)$

$T\left(3000\right)=16\cdot\left(250log\left(3000\right)-844\right)$

Utilizando as propriedades do logaritmo:

$T\left(3000\right)=16\cdot\left(250log(3\bullet1000)-844\right)$

$T\left(3000\right)=16\cdot\left(250(log3+log1000)-844\right)$

$T\left(3000\right)=16\cdot\left(250(0,4+3)-844\right)$

$T\left(3000\right)=16\cdot\left(250\cdot3,4-844\right)$

$T\left(3000\right)=16\cdot\left(850-844\right)$

$T\left(3000\right)=16\cdot6=96\ anos$

Questão 7

(Furb) Considere $f(x)$ = $log_2x$ cujo domínio é o conjunto dos números reais maiores do que zero e g(x) = 4^x-1 cujo domínio é o conjunto dos números reais. Sendo $h(x) = f(g(x)),$ , pode-se afirmar que $h(2) - f(2)$ é um número:

A) ímpar.

B) nulo.

C) múltiplo de 2.

D) múltiplo 3.

E) múltiplo de 5.

Ver resposta

Resposta

Alternativa A

Calculando $f\left(2\right)=log_22=1$

Calculando $h(2)=f(g(2))$

$g\left(2\right)=4^{2-1}=4^1=4$

$h(2)\ =f\left(g\left(2\right)\right)=f\left(4\right)=log_24=2$

Então, temos:

$h\left(2\right)-f\left(2\right)=2-1=1$

1 é um número ímpar.

Questão 8

O pH é utilizado para medir o quanto uma substância é ácida ou básica. Ele pode ser calculado pela fórmula:

$pH=-log\left[H^+\right]$

$[H^+]$ representa a concentração de íons de hidrogênio.

Uma substância pode ser classificada como ácida, básica ou neutra.

• Se a solução apresenta um pH = 7, ela é neutra.

• Se a solução apresenta um pH ≥ 7, ela é básica.

• Se a solução apresenta um pH ≤ 7, ela é ácida.

Sabendo que a concentração de íons de hidrogênio do leite é de 10-7 e do café é de 10-5, podemos afirmar que essas substâncias são, respectivamente:

A) neutra e básica.

B) ácida e neutra.

C) básica e ácida.

D) ácida e básica.

E) neutra e ácida.

Ver resposta

Resposta

Alternativa E

Calcularemos o pH do leite:

$pH_{leite}=-log{10}^{-7}$

$pH_{leite}=-\left(-7\right)log10$

$pH_{leite}=7\ (neutro)\$

Agora, calcularemos o pH do café:

$pH_{leite}=-log{10}^{-5}$

$pHcafé=--5log10$

$pHcafé=5 (ácido)$

Portanto, temos, respectivamente, um pH neutro e um pH ácido.

Questão 9

(Enem 2019) Charles Richter e Beno Gutenberg desenvolveram a escala Richter, que mede a magnitude de um terremoto. Essa escala pode variar de 0 a 10, com possibilidade de valores maiores. O quadro mostra a escala de magnitude local (M_s) de um terremoto que é utilizada para descrevê-lo.

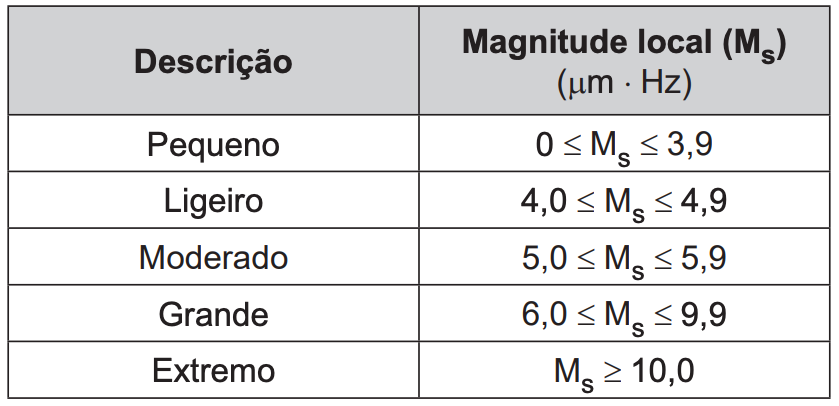
Escala de magnitude local (Ms) de um terremoto

Para calcular a magnitude local, usa-se a fórmula M_s = 3,30 + log(A∙f), em que A representa a amplitude máxima da onda registrada por um sismógrafo em micrômetro (µm) e f representa a frequência da onda, em hertz (Hz). Ocorreu um terremoto com amplitude máxima de 2000 µm e frequência de 0,2 Hz.

Disponível em http://cejarj.cejarj.edu.br. Acesso em: 1 fev 2015 (adaptado).

Utilize 0,3 como aproximação para log 2.

De acordo com os dados fornecidos, o terremoto ocorrido pode ser descrito como

A) pequeno.

B) ligeiro.

C) moderado.

D) grande.

E) extremo.

Ver resposta

Resposta

Alternativa C

Dados: A = 2000 µm e f = 0,2 Hz

Substituindo na fórmula:

$M_s=3,30+log\left(2000\cdot0,2\right)$

$M_s=3,3+log\left(400\right)$

Utilizando as propriedades do logaritmo:

$M_s=3,3+log\left(4\cdot100\right)$

$M_s=3,3+\left(log4+log100\right)$

$M_s=3,3+log2^2+2$

$M_s=3,3+2log2+2$

Sabemos que log2=0,3:

$M_s=3,3+2\cdot0,3+2$

$M_s=3,3+0,6+2$

$M_s=5,9$

De acordo com a tabela, houve um terremoto moderado.

Questão 10

O gráfico a seguir descreve uma função logarítmica:

Gráfico de função logarítmica

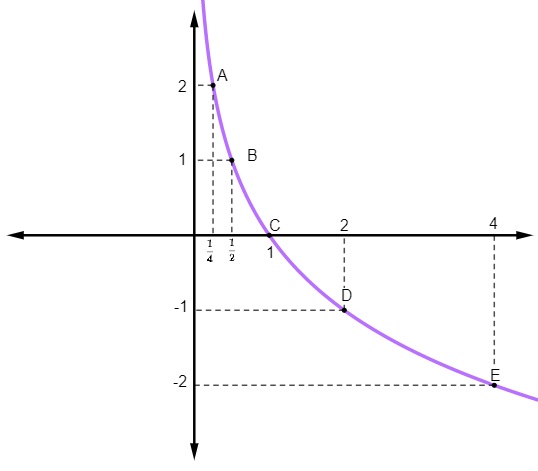
Analisando o gráfico, podemos afirmar que:

I – Essa função é decrescente.

II – A base dessa função é igual a 2.

III – A lei de formação da função é fx=log12x.

Marque a alternativa correta:

A) Somente I é falsa.

B) Somente II é falsa.

C) Somente III é falsa.

D) Todas são verdadeiras.

Ver resposta

Resposta

Alternativa B

I – Verdadeira

Analisando o gráfico, é possível perceber que ele se trata de uma função decrescente, pois à medida que o valor de x aumenta, o valor de y diminui.

II – Falsa

Uma função logarítmica é decrescente quando sua base é menor que 1, logo ela não pode ser igual a 2.

III – Verdadeira

Analisando os pontos da função:

$f\left(x\right)=log_ax$

Quando $x = \frac{1}{2} y = 1$ , temos que:

$1=log_a\frac{1}{2}$

$a^1=\frac{1}{2}$

$a=\frac{1}{2}$

Assim, a lei de formação dessa função será $f\left(x\right)=log_\frac{1}{2}x$ .

Questão 11

(Cesgranrio) Quando a orelha humana é submetida continuamente a ruídos de nível sonoro superior a 85 dB, sofre lesões irreversíveis. Por isso, o Ministério do Trabalho estabelece o tempo máximo diário que um trabalhador pode ficar exposto a sons muito intensos. Esses dados são apresentados a seguir:

• Nível sonoro (dB); 85; tempo máximo de exposição (h); 8

• Nível sonoro (dB); 90; tempo máximo de exposição (h); 4

• Nível sonoro (dB); 95; tempo máximo de exposição (h); 2

• Nível sonoro (dB); 100; tempo máximo de exposição (h); 1

Observa-se, portanto, que a cada aumento de 5 dB no nível sonoro, o tempo máximo de exposição cai para a metade. Sabe-se ainda que, ao assistir a um show de rock, espectadores próximos às caixas de som estão expostos a um nível sonoro de 110 dB. O nível de intensidade sonora (N) é expresso em decibéis (dB) por:

$N=10log\frac{I}{I_0}$

• I = intensidade sonora fornecida pela caixa de som.

• I₀ = intensidade padrão, correspondente ao limiar da audição (para o qual N = 0).

Para o nível de intensidade N = 120 dB, a intensidade sonora fornecida pela caixa de som deverá ser de:

A) 10¹⁴ I₀

B) 10¹²I₀

C) 1200 I₀

D) 120 I₀

E) 12 I₀

Ver resposta

Resposta

Alternativa B

Sendo N = 120, temos:

$N=10log\frac{I}{I_0}$

$120=10log\frac{I}{I_0}$

$\frac{120}{10}=log\frac{I}{I_0}$

Aplicando a definição de logaritmo:

${10}^{12}=\frac{I}{I_0}$

$I={10}^{12}I_0$

Questão 12

(PUC-MG) De acordo com pesquisa feita na última década do século XX, a expectativa de vida em certa região é dada, em anos, pela função E(t) = 12 (150 log(t) – 491), sendo t o ano de nascimento da pessoa. Considerando-se log 2000 = 3,32, uma pessoa dessa região que tenha nascido no ano 2000 tem expectativa de viver:

A) 68 anos

B) 76 anos

C) 84 anos

C) 92 anos

Ver resposta

Resposta

Alternativa C

Calculando a expectativa de vida, temos:

$E\left(t\right)=12150logt–491$

$E\left(2000\right)=12150log2000–491$

$E\left(2000\right)=12150∙3,32–491$