Exercícios sobre função lucro, função receita e função custo
(ACAFE SC/2015) Uma fábrica produz e vende peças para as grandes montadoras de veículos. O custo da produção mensal dessas peças é dado através da função C = 6000 + 14x, onde x é o número de peças produzidas por mês. Cada peça é vendida por R$ 54,00. Hoje, o lucro mensal dessa fábrica é de R$ 6.000,00.
Para triplicar esse lucro, a fábrica deverá produzir e vender mensalmente:
a) o triplo do que produz e vende.
b) 200 unidades a mais do que produz e vende.
c) 50% a mais do que produz e vende.
d) o dobro do que produz e vende.
A função lucro é L(x) = R(x) – C(x). A função custo é C(x) = 6000 + 14x. Já a função receita é R(x) = px, sendo p o preço de mercado e x o número de peças produzidas por mês.
Substituindo a função Custo na função lucro, teremos:
L(x) = R(x) – (6000 + 14x)
Substituindo a função receita nessa função, teremos:
L(x) = px – (6000 + 14x)
Agora faremos dois cálculos distintos: o primeiro para descobrir quantas peças são produzidas mensalmente por essa fábrica e o segundo para descobrir quantas peças devem ser produzidas para triplicar o lucro.
Peças produzidas com lucro normal:
p é o preço de cada peça. Nesse exercício, o preço é 54 reais.
L(x) é o lucro. Nesse caso, R$ 6000,00. A quantidade de peças produzidas para esse lucro será:
6000 = 54x – 6000 – 14x
6000 + 6000 = 54x – 14x
12000 = 40x
x = 12000
40
x = 300
Peças produzidas com lucro triplicado:
p é o preço de cada peça. Nesse exercício, o preço é 54 reais.
L(x) é o lucro. Nesse caso, o lucro almejado é de 18000 reais, exatamente o triplo do lucro mensal já alcançado por essa fábrica. Então, a equação, com as devidas substituições, fica assim:
18000 = 54x – 6000 – 14x
18000 + 6000 = 54x – 14x
24000 = 40x
x = 24000
40
x = 600
Observe que 600 é o número de peças produzidas por mês com o lucro mensal triplicado e 300 é o número de peças produzidas por mês com o lucro mensal normal. Dessa forma, sabendo que 600 é o dobro de 300, para triplicar o lucro da fábrica, ela deve dobrar sua produção e vendas.
Alternativa D.
(UERN/2015) O gráfico apresenta o lucro de uma empresa no decorrer do primeiro semestre de determinado ano:
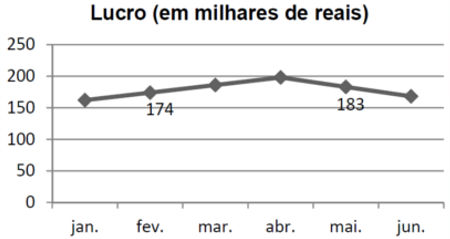
Os economistas dessa empresa dividiram esse período em dois: primeiro período, de janeiro a abril, em que há um crescimento linear nos lucros; e segundo período, de abril a junho, em que há uma queda nos lucros de R$ 15 mil ao mês. A partir dessas informações, é correto afirmar que o lucro obtido no mês de janeiro foi:
a) R$ 158.000,00.
b) R$ 162.000,00.
c) R$ 164.000,00.
d) R$ 168.000,00.
Para resolver esse exercício, analisaremos o gráfico para descobrir qual foi o lucro dessa empresa no mês de abril e utilizaremos as siglas: La = lucro de abril, Lj = Lucro de janeiro, Lf = Lucro de fevereiro e Lm = Lucro de março.
De abril para maio, o lucro caiu 15 mil, pois ele cai justamente esse valor por mês.
La = 183000 + 15000 = 198000.
Logo, em abril, houve um lucro de R$ 198000,00.
Entre fevereiro e abril, teremos:
La – Lf = 24000
Como pôde ser visto, o lucro dessa empresa cresceu R$ 24000,00 em dois meses. Isso quer dizer que, se em dois meses essa empresa teve um crescimento de R$ 24000,00, em um mês, utilizando regra de três, o crescimento foi de R$ 12000,00. Portanto,
Lj = Lf – 12000
Lj = 174000 – 12000
Lj = 162000
O lucro em janeiro foi de R$ 162000,00.
Alternativa B.
Supondo que o custo total para fabricar sapatos seja dado por C(x) = x3 + 100, em reais, determine:
a) O custo fixo;
b) O preço variável;
c) O custo de fabricação de 10 sapatos;
d) O custo médio da produção dos 10 primeiros sapatos.
a) O custo fixo é a parte “não variável” da função. Portanto, o custo fixo é R$ 100,00.
b) O custo variável é de x3 reais.
c) Para calcular o custo da fabricação de 10 sapatos, basta substituir x por 10 na função custo:
C(10) = 103 + 100
C(10) = 1000 + 100
C(10) = 1100
Portanto, o custo para fabricar 10 sapatos é R$ 1100,00.
d) O custo médio da produção dos dez primeiros sapatos é o custo para produzi-los dividido pelo número de sapatos produzidos.
Custo médio = 1100
10
Custo médio = 110
Logo, cada um dos primeiros 10 sapatos custou R$ 110,00 para ser produzido.
A produção de um determinado item tem um custo C(x) = 5x + 50. Sabendo que cada um dos itens custa R$ 30,00, quantos deles devem ser produzidos para que o lucro seja de R$ 600,00?
L(x) = R(x) – C(x)
L(x) = px – (5x + 50)
600 = 30x – 5x – 50
600 + 50 = 30x – 5x
650 = 25x
x = 650
25
x = 26
Devem ser produzidos 26 itens para que o lucro seja de R$ 600,00.
