Exercícios sobre Geratriz de uma Dízima Periódica
Exercícios sobre a geratriz de uma dízima periódica podem ser resolvidos através de noções básicas de equações e frações.
Publicado por: Amanda Gonçalves RibeiroQuestões
-
Questão 1
Apresente o resultado da expressão na forma fracionária:
0,66666... + 0,25252525... – 0,77777...
Há duas opções de resolução para esse exercício: a primeira é encontrar a fração geratriz de cada dízima periódica e resolver a expressão utilizando as frações. A segunda opção é encontrar a fração geratriz do resultado da expressão. Para realizarmos menos cálculos, optaremos pela segunda opção, mas vale lembrar que chegaríamos ao mesmo resultado se optássemos pela primeira sugestão. Vamos então realizar a soma inicial através do algoritmo da adição, lembrando que é necessário colocar “vírgula embaixo de vírgula”:
0,66666666...
+0,25252525...
0,91919191...Desse resultado, vamos subtrair 0,7777777...
0,91919191...
– 0,777777777...
0,14141414...Vamos agora encontrar a fração geratriz de 0,14141414...
x = 0,14141414...
Multiplicando ambos os lados da equação por 100, temos:
100.x = 14,141414...
Vamos então subtrair dessa equação sua antecedente:
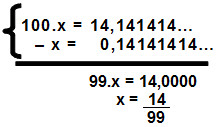
Portanto, a equação tem como resultado a fração 14/99.
-
Questão 2
Se x = 0,22222... e y = 2,595959..., calcule o valor da soma dos algarismos do numerador da fração x.y
Vamos primeiramente encontrar a fração geratriz de x:
x = 0,22222...
Devemos agora multiplicar ambos os lados da equação por 10:
10 . x = 2,22222...
Subtraindo dessa equação a anterior, teremos:
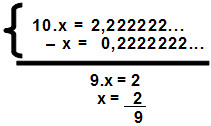
Vamos encontrar a fração geratriz de y:
y = 2,595959595...
Multiplicando ambos os lados da equação por 100:
100 . y = 259,5959595...
Subtraindo dessa equação a anterior, o resultado será:
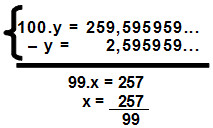
Vamos agora calcular o produto de x.y:
x.y = 2 . 257 = 514
9 99 891Encontramos o produto de x.y, precisamos então calcular a soma dos algarismos do numerador dessa fração, portanto, 5 + 1 + 4 = 10.
-
Questão 3
(PUC – RJ) A soma 1,3333... + 0,1666666... é igual a:
a) 1/2
b) 5/2
c) 4/3
d) 5/3
e) 3/2
Vamos encontrar a fração geratriz dos dois números decimais do exercício. Para o número 1,3333..., temos:
x = 1,3333...
Multiplicando ambos os lados da equação por 10:
10x = 13,3333...
Vamos agora subtrair a equação anterior da última, da seguinte forma:
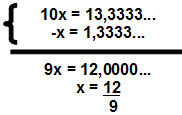
Simplificando o numerador e o denominador por 3:
x = 4
3Vamos fazer o mesmo processo para 0,166666...
x = 0,16666...
Multiplicando ambos os lados da equação por 10, e novamente por 10:
10x = 1,6666...
100x = 16,6666...Subtraindo a última equação da equação anterior, o resultado será o seguinte sistema:
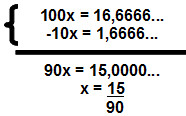
Simplificando a fração final por 15:
x = 1
6Agora, em vez de realizarmos a soma de números decimais, faremos a soma das frações geratrizes:
1,3333... + 0,16666... = 4 + 1 = 2.4 +1.1 = 9 = 3
3 6 6 6 2Portanto, a alternativa correta é a letra E.
-
Questão 4
Se x = 0,1212..., o valor numérico da expressão
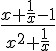 é:
é:a) 1/37
b) 21/37
c) 33/37
d) 43/37
e) 51/37
Para resolver a expressão, é necessário que antes escrevamos a dízima periódica como sua fração geratriz:
x = 0,1212...
100x = 12,1212...Subtrai-se essa equação da anterior:
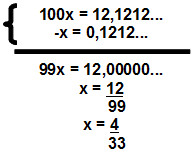
Agora se substitui o valor encontrado na expressão:
.jpg)
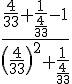
As propriedades operatórias de fração são aplicadas:
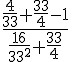
Aplica-se o mínimo múltiplo comum no numerador e no denominador da fração maior:
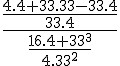 =
=  =
= 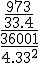 =
= 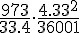 =
= 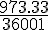 =
= 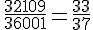
Após sucessivas simplificações, o resultado da expressão é 33/37, alternativa C.