Exercícios sobre grandezas inversamente proporcionais
Esta lista tem questões resolvidas sobre as grandezas inversamente proporcionais, com diversos problemas que podem ser encontrados no cotidiano.
Publicado por: Raul Rodrigues de OliveiraQuestões
-
Questão 1
Durante as eleições, uma gráfica recebeu um pedido muito grande para realizar a produção de material de campanha. Estimou-se que as 3 máquinas levariam 24 horas para realizar todo o serviço. Supondo que uma dessas máquinas estrague antes de iniciar o serviço, qual será o tempo necessário para atender essa demanda?
A) 30 horas
B) 20 horas
C) 26 horas
D) 36 horas
E) 40 horas
Alternativa D
Sabemos que, ao reduzir-se a quantidade de máquinas, o tempo aumentará, logo, essa situação descreve grandezas inversamente proporcionais. Montando a tabela, temos que:
Quantidade de máquinas
Tempo
3
24
2
x
Multiplicando reto:
2x = 3 · 24
2x = 72
x = 72 : 2
x = 36 horas
-
Questão 2
Conhecemos como quadrilátero um polígono que possui 4 lados. Sabendo que a soma dos ângulos internos de um quadrilátero é sempre igual a 360º e que um quadrilátero possui ângulos inversamente proporcionais a 2, 3, 4, e 5, então, o valor do menor ângulo dessa quadrilátero é, aproximadamente:
A) 56º
B) 64º
C) 96º
D) 120º
E) 140º
Alternativa A
Sejam a, b, c, d os ângulos, sabemos que a + b + c + d = 360°.
Como os ângulos são inversamente proporcionais a 2, 3, 4 e 5, então, temos que:
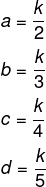
Substituindo esses valores na equação, temos que:
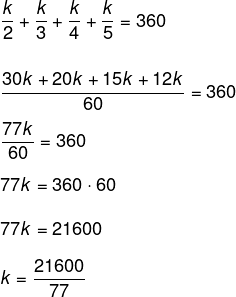
Como nós queremos o menor ângulo, temos que d = k/5, então, temos que:
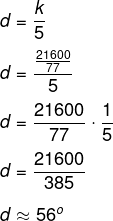
-
Questão 3
Das situações abaixo, marque aquela que descreve duas grandezas inversamente proporcionais:
A) Quantidade de pessoas em um churrasco e a quantidade de carne necessária.B) Número de habitantes em uma cidade e a taxa de mortalidade.
C) Velocidade de um automóvel e a distância percorrida em um mesmo intervalo de tempo.
D) Comprimento da altura e a área de um polígono.
E) Vazão de um ralo e o tempo necessário para esvaziar um reservatório.
Alternativa E
Quanto maior a vazão da água para esvaziar o reservatório, menor será o tempo necessário para tanto, ou seja, essas grandezas são inversamente proporcionais.
-
Questão 4
(IF-SP) Para fazer uma viagem, levamos em consideração duas grandezas: velocidade do meio de transporte e tempo de viagem. Essas duas grandezas são
A) completamente proporcionais.
B) desproporcionais.
C) diretamente proporcionais.
D) subitamente proporcionais.
E) inversamente proporcionais.
Alternativa E
A relação entre velocidade e tempo nessa situação é inversamente proporcional, pois se eu aumento a velocidade, o tempo que eu levo para chegar até o destino será menor.
-
Questão 5
Em uma empresa, os três melhores funcionários serão premiados e dividirão um valor de R$ 38.200 de forma inversamente proporcional ao número de vendas perdidas durante o ano.
Sabendo que o funcionário que ficou em primeiro lugar perdeu 28 vendas, o segundo, 32, e o terceiro, 36, o valor recebido pelo funcionário que perdeu menos vendas é igual a:
A) R$ 8600
B) R$ 9000
C) R$ 10.500
D) R$ 11.200
E) R$ 14.400
Alternativa E
Sejam a, b, c a quantidade recebida por funcionário, sabemos que a + b + c = 38.200. Montando as proporções, temos que:
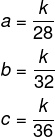
Substituindo na soma, temos que:
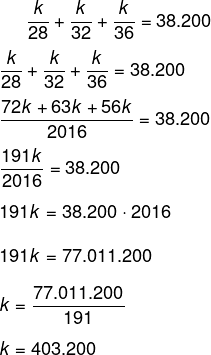
Agora que encontramos o valor de k, queremos o valor recebido pelo funcionário que perdeu menos vendas, para isso, basta dividir k por 28.
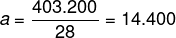
-
Questão 6
Um triângulo possui ângulos internos proporcionais aos números 1, 3 e 6, então, o valor do seu maior ângulo é:
A) 30°B) 60°
C) 90°
D) 120°
E) 150°
Alternativa D
Sejam a, b e c os ângulos internos do triângulo, e sabendo que a soma deles é sempre igual a 180º, então, temos que a + b + c = 180º. Como eles são inversamente proporcionais a 1, 3 e 6, escreveremos a proporção:
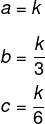
Substituindo os valores de a, b e c, temos que:
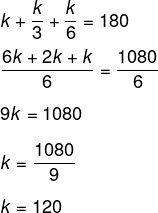
Agora que sabemos o valor de k, o maior ângulo é a = k, então, a = 120º.
-
Questão 7
Marque a alternativa que melhor define quando duas grandezas são inversamente proporcionais:
A) Duas grandezas, A e B, são inversamente proporcionais quando existe uma relação entre elas, em uma determinada situação, que faz com que na medida em que a grandeza A aumenta o seu valor, a grandeza B também aumente, na mesma proporção. Um exemplo disso é a quantidade de partidas vencidas e a pontuação de um time no campeonato.
B) Duas grandezas são inversamente proporcionais quando elas não possuem nenhuma relação, ou seja, se uma das grandezas aumentar o seu valor, a outra pode aumentá-lo ou diminui-lo.
C) Duas grandezas são inversamente proporcionais quando na medida em que o valor de uma delas aumenta, o valor da outra diminui na mesma proporção. Um exemplo disso é a relação entre a velocidade e o tempo gasto em um percurso fixo.
D) Duas grandezas nunca serão inversamente proporcionais, pois existem grandezas diretamente proporcionais e grandezas que não se relacionam e são improporcionais.
Alternativa C
A alternativa que define corretamente as grandezas inversamente proporcionais é a alternativa C.
-
Questão 8
Durante a pandemia de covid-19, os cientistas buscaram sempre relacionar grandezas para compreender melhor o fenômeno. Os estatísticos perceberam que existe uma relação entre as grandezas: número de vacinados e quantidade de casos graves. Como era de se esperar, com metade da população vacinada, o número de casos graves da doença caiu também pela metade. Sabendo da eficácia da vacina, podemos afirmar que as grandezas citadas se relacionam de forma
A) inversamente proporcional.
B) diretamente proporcional.
C) desproporcional.
D) subitamente proporcional.
E) essas grandezas se relacionam, mas não há proporção entre elas.
Alternativa A
Note que se o número de vacinados dobrou e a quantidade de casos graves caiu pela metade, existe então proporção entre as grandezas e de forma inversa.
-
Questão 9
(Enem 2019) Para contratar três máquinas que farão o reparo de vias rurais de um município, a prefeitura elaborou um edital que, entre outras cláusulas, previa:
• Cada empresa interessada só pode cadastrar uma única máquina para concorrer ao edital;
• O total de recursos destinados para contratar o conjunto das três máquinas é de R$ 31 000;
• O valor a ser pago a cada empresa será inversamente proporcional à idade de uso da máquina cadastrada pela empresa para o presente edital.
As três empresas vencedoras do edital cadastraram máquinas com 2, 3 e 5 anos de idade de uso.
Quanto receberá a empresa que cadastrou a máquina com maior idade de uso?
A) R$ 3100
B) R$ 6000
C) R$ 6200
D) R$ 15.000
E) R$ 15.500
Alternativa B
Cada empresa receberá de forma inversamente proporcional ao tempo de uso da máquina, então, sejam x, y, z o recebimento de cada empresa, temos que:
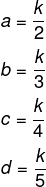
Sabemos que a soma x + y + z = 31.000, logo, temos que:
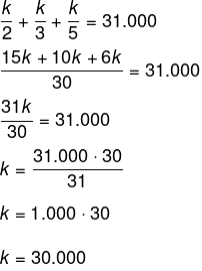
Conhecendo o valor de k, 5 anos são a maior idade de uso da máquina por uma empresa, então, basta calcular k dividido por 5.
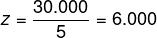
-
Questão 10
Uma prestadora de serviços em construção civil foi contratada para a reforma de um condomínio. A previsão é que, com 6 funcionários, a reforma levaria 18 dias para ser feita caso fossem contratados 3 funcionários a mais. O tempo necessário para realizar a reforma é de:
A) 10 dias
B) 11 dias
C) 12 dias
D) 13 dias
E) 14 dias
Alternativa C
As grandezas são: quantidade de funcionários e dias. Sabemos que essas grandezas são inversamente proporcionais. Montando a regra de três, temos que:
Quantidade de funcionários
Tempo
6
18
9
x
9x = 6 · 18
9x = 108
x = 108 : 9
x = 12 dias
-
Questão 11
Para fazer uma viagem da cidade A para a cidade B, um automóvel gasta cerca de 4 horas, a uma velocidade média de 75 km/h. Caso fosse necessário que essa viagem fosse feita em 3 horas, o tempo gasto seria de:
A) 86 km/h
B) 90 km/h
C) 95 km/h
D) 100 km/h
E) 110 km/h
Alternativa D
As grandezas são: quantidade de velocidade e tempo. Sabemos que essas grandezas são inversamente proporcionais. Montando a regra de três, temos que:
Velocidade
Tempo
75
4
x
3
3x = 4 · 75
3x = 300
x = 300 : 3
x = 100 km/h
-
Questão 12
Durante a produção de sabonete líquido para sua família, Márcia decidiu dividir igualmente entre os seus 5 filhos a produção, ficando cada um com 2,7 litros. Como a quantidade que cada um levaria estava grande, ela decidiu que, além dos 5 filhos, ela ficaria com uma parte e doaria também para as suas 3 vizinhas, de modo que cada um receba a mesma quantidade, então, cada um receberá um total de:
A) 1,2 L
B) 1,5 L
C) 1,8 L
D) 2,0 L
E) 2,5 L
Alternativa B
As grandezas são: quantidade de pessoas e quantidade de sabonete, e elas são inversamente proporcionais, pois se aumentarmos a quantidade de pessoas, cada pessoa receberá menos do que receberia antes.
Montando a regra de três, temos que:
Quantidade de sabão
Tempo
2,7 litros
5
x
9
9x = 2,7 · 5
9x = 13,5
x = 13,5 : 9
x = 1,5
Cada pessoa receberá 1,5 litros.