Exercícios sobre inequações logarítmicas
Resolva a inequação logarítmica log10 (x² + 2) > log10 (2x – 1).
Vamos, inicialmente, verificar as condições de existência dos logaritmos:
| x² + 2 > 0 x² > – 2 x > √– 2 A inequação não possui solução real. |
x – 1 > 0 2x > 1 x > 1 2 |
Como os logaritmos possuem a mesma base, podemos desconsiderá-los e estabelecer a inequação apenas com os logaritmandos:
log10 (x² + 2) > log10 (2x – 1)
x² + 2 > 2x – 1
x² – 2x + 2 + 1 > 0
x² – 2x + 3 > 0
Através da fórmula de Bhaskara, podemos determinar as raízes de x² – 2x + 3 = 0:
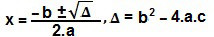
Δ = (– 2)² – 4∙1∙3
Δ = 4 – 12
Δ = – 8
Como Δ < 0, a equação não possui raízes reais. Portanto, a inequação x² – 2x + 3 > 0 também não possui um intervalo real. Pelas condições de existência, podemos concluir que a única solução possível para log10 (x² + 2) > log10 (2x – 1) é x > ½.
Determine o conjunto solução da inequação logarítmica:
log0,5 (x – 5) – log0,5 (x) > log0,5 (x + 3)
Vamos verificar as condições de existência dos logaritmos:
| x – 5 > 0 x > 5 |
x > 0 | x + 3 > 0 x > – 3 |
A subtração de logaritmos de mesma base equivale a um único logaritmo cujo logaritmando é o quociente dos logaritmandos anteriores e cuja base é preservada.
log0,5 (x – 5) – log0,5 (x) > log0,5 (x + 3)
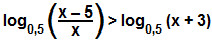
Como os logaritmos possuem a mesma base, podemos estabelecer uma desigualdade apenas entre os logaritmandos. Nesse caso, como a base é menor que 1, inverte-se o sinal da desigualdade:
x – 5 < x + 3
x
x – 5 < x ∙ (x + 3)
x – 5 < x² + 3x
– x² + x – 3x – 5 < 0
– x² – 2x – 5 < 0
x² + 2x + 5 < 0
Através da fórmula de Bhaskara, podemos determinar as raízes de x² + 2x + 5 = 0:
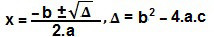
Δ = 2² – 4∙1∙5
Δ = 4 – 20
Δ = – 16
Como Δ < 0, a equação não possui raízes reais. Logo, x² + 2x + 5 < 0 também não possui um intervalo real. Para determinar o conjunto solução, partiremos então das condições de existência, que fornecem as seguintes soluções para comparação:
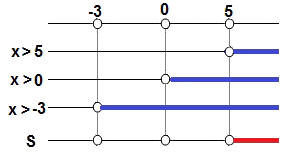
Solução da questão 2
Portanto, o conjunto solução de log0,5 (x – 5) – log0,5 (x) > log0,5 (x + 3) é dado por S = {x 
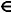
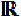| x > 5}.
(Fuvest) O conjunto dos números reais x que satisfazem a inequação log2 (2x + 5) – log2 (3x – 1) > 1 é o intervalo:
a) ]–∞, – 5/2[
b) ]7/4, ∞[
c) ]–5/2, 0[
d) ]1/3, 7/4[
e) ]0, 1/3[
Primeiramente vamos verificar as condições de existência dos logaritmos:
| 2x + 5 > 0 2x > – 5 x > – 5 2 |
3x – 1 > 0 3x > 1 x > 1 3 |
Vamos agora substituir o 1 por log2 2, que são equivalentes. Teremos então a seguinte inequação:
log2 (2x + 5) – log2 (3x – 1) > log2 2
Sabendo que a subtração de logaritmos de mesma base pode ser expressa com um logaritmo cujo logaritmando é o quociente dos logaritmandos anteriores, temos:
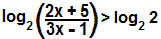
Podemos agora desconsiderar os logaritmos e estabelecer a desigualdade apenas entre os logaritmandos:
2x + 5 > 2
3x – 1
2x + 5 > 2 ∙ (3x – 1)
2x + 5 > 6x – 2
2x – 6x > – 2 – 5
– 4x > – 7
4x < 7
x < 7
4
Comparando as soluções:
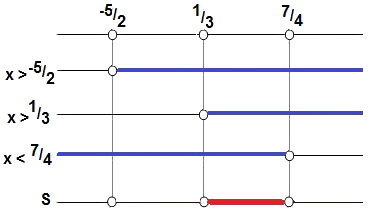
Solução da questão 3
Portanto, a alternativa que compreende o intervalo correto é a letra d, que indica ]1/3, 7/4[.
(Ufop – MG) Resolva a inequação log2 (x – 3) + log2 (x – 2) < 1.
Analisando as condições de existência dos logaritmos, temos:
| x – 3 > 0 x > 3 |
x – 2 > 0 x > 2 |
Como log2 2 = 1, podemos reescrever a inequação da seguinte forma:
log2 (x – 3) + log2 (x – 2) < log2 2
Se a soma de logaritmos de mesma base equivale ao logaritmo cujo logaritmando é o produto dos logaritmandos anteriores, temos:
log2 [(x – 3) ∙ (x – 2)] < log2 2
Desconsiderando os logaritmos, podemos manter a desigualdade apenas entre os logaritmandos:
(x – 3) ∙ (x – 2) < 2
x² – 3x – 2x + 6 < 2
x² – 5x + 4 < 0
Podemos utilizar a fórmula de Bhaskara para determinar as raízes de x² – 5x + 4 = 0:
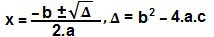
Δ = (– 5)² – 4∙1∙4
Δ = 25 – 16
Δ = 9
x = – (– 5) ± √9
2∙1
x = 5 ± 3
3
x' = 5 + 3 = 8 = 4
2 2
x'' = 5 – 3 = 2 = 1
2 2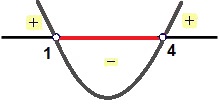
Análise do sinal de x² – 5x + 4 < 0ões, chegamos ao seguinte quadro: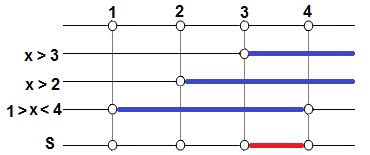
Solução da questão 4
Portanto, o conjunto solução de log2 (x – 3) + log2 (x – 2) < 1 é S = ]3, 4[
