Exercícios sobre Matriz Transposta
Os exercícios sobre Matriz transposta têm grande importância no estudo de matrizes. Através deles trabalhamos vários conceitos, como simétrica e inversa.
Publicado por: Amanda Gonçalves RibeiroQuestões
-
Questão 1
Sendo A =
 e B =
e B = 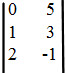 , determine:
, determine:a) 2A + At
b) 3Bt
c) (At)t
a) Nós multiplicaremos todos os elementos da matriz A por 2 e, em seguida, somaremos a essa matriz a transposta da matriz A, ou seja, a matriz A com os elementos das linhas trocados pelos elementos das colunas e vice-versa.
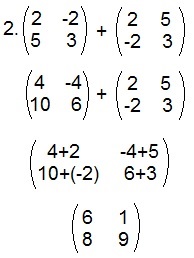
b) Vamos trocar as linhas pelas colunas da matriz B, escrevendo assim a sua matriz transposta. Depois de encontrar a matriz resultante, multiplicaremos todos os elementos por 3.

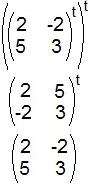
c) Primeiramente, nós encontraremos a transposta da matriz A. Feito isso, repetiremos o processo. Facilmente vemos que (At)t = A.
-
Questão 2
Resolva a equação Xt + 2A = – B, se A =
 e B =
e B = 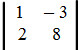
Inicialmente, no primeiro membro da equação, vamos multiplicar os elementos da matriz A por 2 e, no segundo membro da equação, vamos multiplicar a matriz B por – 1. Feito isso, mudaremos os elementos da matriz (2.A) para o segundo membro da equação com o sinal de menos. Realizaremos, então, o cálculo (– B) – (2.A) no segundo membro da equação, encontrando assim a matriz Xt.
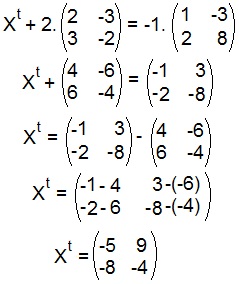
-
Questão 3
(PUC-GO) Analise a afirmação seguinte: Se A é uma matriz quadrada, então A + AT é uma matriz simétrica e A – AT é uma matriz antissimétrica.

Portanto, a afirmativa é verdadeira.
-
Questão 4
(Fei - SP) Dada a Matriz A =
 , sendo At sua transposta, o determinante da matriz A.At é:
, sendo At sua transposta, o determinante da matriz A.At é:a) 1
b) 7
c) 14
d) 49
Inicialmente, nós encontramos a matriz transposta a A. Em seguida, fazemos a multiplicação da matriz A pela sua transposta. Como podemos ver a seguir:
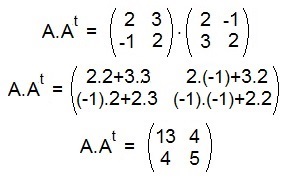
Vamos agora calcular o determinante da matriz encontrada:
Det (A.At) = 13.5 – 4.4
Det (A.At) = 65 – 16
Det (A.At) = 49Portanto, a alternativa correta é a letra d.