Exercícios sobre máximo divisor comum
Em um canil, há 15 Chihuahuas, 40 Yorkshires e 75 Poodles. O dono gostaria de organizar os cães em grupos, de modo que cada grupo possua o mesmo número de cães e cada raça esteja igualmente distribuída nos grupos. Qual é o número máximo de grupos que podem ser formados com quantidades iguais de cada raça? Quantos cães de cada raça haverá por grupo?
Para descobrir o número máximo de grupos que podem ser formados com quantidades iguais de cada raça, é necessário calcular o máximo divisor comum entre 15, 40 e 75, isto é, o MDC (15, 40, 60). Esse cálculo pode ser feito através do método das divisões sucessivas. Como estamos trabalhando com três números, com dois desses cálculos, já podemos ter certeza do resultado:
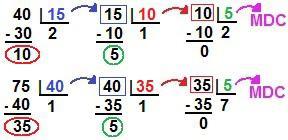
Cálculo do MDC da questão 2 através do método das divisões sucessivas
Portanto, é possível formar cinco grupos com os cachorros do canil. Dividindo a quantidade de cachorros de cada raça igualmente nos cinco grupos, teremos:
Chihuahuas → 15 : 5 = 3
Yorkshires → 40 : 5 = 8
Poodles → 75 : 5 = 15
Então haverá cinco grupos de cães, e cada grupo será composto por 3 Chihuahuas, 5 Yorkshires e 15 Poodles.
Um homem comprou duas tábuas de madeira para a reforma de sua casa. Para aproveitar a oferta da loja, ele comprou uma tábua de 3,5 m e outra de 2,1 m, pois elas estavam de liquidação. Precavido, ele só comprou essas tábuas de tamanhos diferentes depois que o vendedor garantiu que ele conseguiria dividir as duas tábuas em pedaços de mesmo tamanho. Qual é o maior tamanho que as partes poderão ter? Com esse comprimento, quantas partes da tábua o homem terá?
Para iniciar a resolução dessa questão, vamos considerar o comprimento das tábuas em centímetros, isto é, 350 cm e 210 cm. Para encontrar o maior comprimento possível para as partes da tábua, calcularemos o MDC (350, 210) através do método das divisões sucessivas:
Cálculo do MDC da questão 2 através do método das divisões sucessivas
Portanto, o MDC (350, 210) = 70. Isso garante que o homem poderá cortar as tábuas em partes com 70 cm. Como 350 : 70 = 5 e 210 : 70 = 3, podemos concluir que o homem terá oito pedaços de tábua com 70 cm de comprimento.
(UFU) Considere a função f: N → N, (onde N representa o conjunto dos números naturais) dada por f(n) = mdc (2n + 4, 4n + 2). Então, o valor mínimo de f é igual a:
a) 4
b) 1
c) 6
d) 2
e) 8
Para identificar a função f, precisamos encontrar o máximo divisor comum (MDC) entre 2n + 4 e 4n + 2. Para determinar esse MDC, utilizaremos o método das divisões sucessivas:
Cálculo do MDC da questão 3 através do método das divisões sucessivas
Na última divisão, aquela que apresenta resto zero, o divisor é o 2. Portanto, o MDC (2n + 4, 4n + 2) é igual a 2. A alternativa correta é a letra d.
(Bio – Rio) O MDC entre 2³.3.5² e 2².3.7² é igual a:
a) 6
b) 12
c) 60
d) 50
e) 300
Para solucionar essa questão, não é necessário utilizar o método das divisões sucessivas. Como os números foram escritos como produtos de números primos, basta compará-los, pois os fatores que se repetem em ambos os números indicam o MDC:
2³.3.5² = 2.2.2.3.5.5
2².3.7² = 2.2.3.7.7
Observe que nos dois números vemos a repetição do produto 2.2.3, que resulta em 12. Podemos concluir que o MDC (2³.3.5², 2².3.7²) é igual a 12. Portanto, a alternativa correta é a letra b.
