Exercícios sobre multiplicação de polinômios
O produto entre os polinômios A e B, sendo que A = 2x + 4 e B = 2x – 4, é igual a:
A) 4x² - 16
B) 4x² + 16
C) 4x² + 8x + 16
D) 4x² - 8x – 16
E) 4x + 8
Alternativa A
Calculando o produto, temos que:
\((2x+4)(2x-4)\)
Aplicando a propriedade distributiva:
\(2x^2-8x+8x-16\)
\(4x^2-16\)
Um retângulo possui lados medindo x + 2y e 3x – y. A medida da área desse retângulo pode ser expressa pelo polinômio:
A) 4x – 2y
B) 3x² - 2y²
C) 3x² + 3yx – y²
D) 3x² + 5xy – 2y²
E) 3x² + 6xy +2y²
Analise a imagem a seguir:
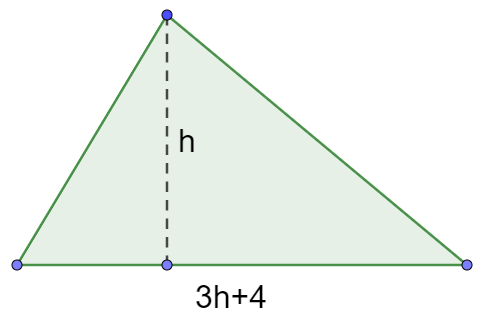
O polinômio que nos dá a área desse triângulo em função de h é:
A) 3h² + 4
B) 7h²
C) 4h² + 4h
D) \(\frac{3}2 h^2+2h\)
E) \(3,5h^2\)
Alternativa D
Sabemos que a área do triângulo é igual ao produto da base pela sua altura divido por 2. Nessas condições, temos que:
\(A=\frac{(3h+4)⋅h}2\)
\(A=\frac{3h^2+4h}2\)
\(A=\frac{3}2 h^2+2h\)
A área do círculo é calculada pela expressão \(A=πr^2\). Se um determinado círculo teve seu raio aumentado em uma unidade, então a expressão que nos dá a área desse círculo em função do raio é:
A) \(A=r^2+2r+π\)
B) \(A=πr^2+π+1\)
C) \(A=r^2+2rπ+1\)
D) \(A=r+2r+1+π\)
E) \(A=πr^2+2rπ+π\)
Alternativa E
Sabemos que o raio será r + 1, então temos que:
\(A=π(r+1)^2\)
\(A=π(r+1)⋅(r+1)\)
\(A=π(r^2+r+r+1)\)
\(A=π(r^2+2r+1)\)
\(A=πr^2+2rπ+π\)
A seguir, temos a imagem de um paralelepípedo retângulo.
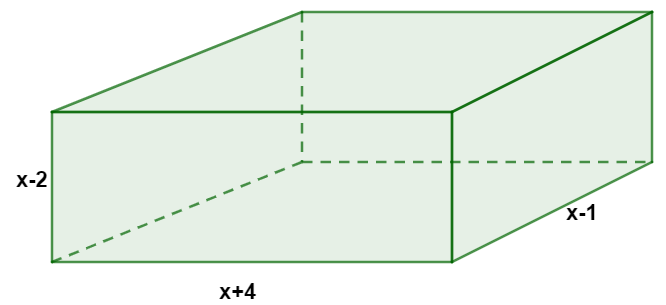
Se o volume do paralelepípedo é igual ao produto entre os seus lados, o polinômio que nos dá o volume desse sólido é:
A) \( x^5+10x+8\)
B) \(x^3+x^2-10x+8\)
C) \(x^3+2x^2+2x+-6\)
D) \(8x^2-10x+3\)
E) \(x^3+x^2+10x+8\)
Alternativa B
Calculando o volume, temos que:
\(V=(x+4)(x-1)(x-2)\)
\(V=(x^2-x+4x-4)(x-2)\)
\(V=(x^2+3x-4)(x-2)\)
\(V=x^3-2x^2+3x^2-6x-4x+8\)
\(V=x^3+x^2-10x+8\)
Dados os polinômios x = 2x² + x – 3 e y = x³ - 2x + 1, o valor da expressão 2x + 3y é o polinômio:
A) \(3x^3-4x-3\)
B) \( 3x^3-3\)
C) \(3x^3+4x^2-4x-3\)
D) \(3x^3+8x^2-4x\)
E) \( 3x^3+4x^2-4x+3\)
Alternativa C
Calculando a expressão, temos que:
\(2x+3y=2(2x^2+x-3)+3(x^3-2x+1)\)
\(2x+3y=4x^2+2x-6+3x^3-6x+3\)
\(2x+3y=3x^3+4x^2-4x-3\)
Conhecendo os polinômios P = 4x² + 2x – 3x e Q = 9x³ + 12x – 3, o grau do polinômio \(P⋅Q\) será igual a:
A) 36
B) 13
C) 6
D) 5
E) 3
Alternativa D
Para calcular o grau do polinômio gerado a partir do produto de P por Q, basta calcularmos o grau do produto entre os monômios de maior grau: no P é 4x² e no Q é 9x³.
\(4x^2⋅9x^3=36x^5\)
Sabemos, então, que o grau do polinômio P⋅Q é igual a 5.
Sobre a multiplicação de polinômios, julgue as afirmativas a seguir:
I – O produto de um polinômio de grau 3 com um polinômio de grau 2 gera um polinômio de grau 6.
II – O produto entre os polinômios (x + 2) e (x – 2) gera um trinômio.
III – O quadrado do polinômio (x – 3) é o trinômio x² - 6x + 9.
Marque a alternativa correta:
A) Somente a afirmativa I é verdadeira
B) Somente a afirmativa II é verdadeira
C) Somente a afirmativa III é verdadeira
D) Somente as afirmativas I e III são verdadeiras
E) Somente as afirmativas II e III são verdadeiras
Alternativa C
I – O produto de um polinômio de grau 3 com um polinômio de grau 2 gera um polinômio de grau 6. (falsa)
O grau do produto é igual à soma dos graus dos polinômios, ou seja, 3 + 2 = 5.
II – O produto entre os polinômios (x + 2) e (x – 2) gera um trinômio. (falsa)
(x+2)(x-2) = x² +2x – 2x – 4 = x² - 4
A resposta é um binômio.
III – O quadrado do polinômio (x – 3) é o trinômio x² - 6x + 9. (verdadeira)
(x-3)² = (x-3)(x-3) = x² -3x -3x + 9 = x² - 6x + 9.
O produto entre os polinômios P(x) = (k+2)x² + 3kx + 8 e Q(x) = -2x² + x – 2 é um polinômio de grau 2, denotado por R(x), então o valor de R(-1) é:
A) -2
B) 2
C) -4
D) 6
E) 8
Alternativa D
Calculando o produto, temos que:
\(((k+2) x^2+3kx+8)⋅(x–2)\)
\((k+2) x^3-(-2k-4) x^2+3kx^2-6kx+8x-16 \)
Sabemos que k + 2 = 0, então k = - 2.
Logo, temos que:
\((-2+2) x^3-(2⋅(-2)-4) x^2+3⋅(-2) x^2-6⋅(-2)x+8x+16\)
\(0x^3-8x^2-6x^2-12x+8x+16\)
\(R(x)=-14x^2-4x+16\)
Calculando x = -1:
\(R(-1)=-14⋅1-4⋅(-1)+16\)
\(R(-1)=-14+4+16\)
\(R(-1)-14+20\)
\(R(-1)=6\)
Se os lados de um quadrado medindo x + 5 forem dobrados, então a nova área desse quadrado pode ser expressa pelo polinômio:
A) \(2x+10\)
B) \( 4x^2 +100\)
C) \(4x^2 - 100\)
D) \( 4x^2+20x+100\)
E) \( 4x^2+40x+100\)
Alternativa E
Se dobrarmos a medida do lado, então ela pode ser expressa por:
\(2(x+5)\)
\(2x+10\)
A área do quadrado é igual ao quadrado do lado, então a área desse quadrado será:
\((2x+10)^2\)
\((2x+10)(2x+10)\)
\(4x^2+20x+20x+100\)
\(4x^2+40x+100\)
Ao multiplicar dois polinômios que possuem respectivamente grau 3 e grau 4, o resultado será um polinômio de grau:
A) 7
B) 12
C) 26
D) 64
E) 81
Alternativa A
O grau do produto será a soma dos graus de cada um dos fatores, ou seja, a soma dos graus dos polinômios: 3 + 4 = 7.
(Enem 2012) Um forro retangular de tecido traz em sua etiqueta a informação de que encolherá após a primeira lavagem, mantendo, entretanto, seu formato. A figura a seguir mostra as medidas originais do forro e o tamanho do encolhimento (x) no comprimento e (y) na largura. A expressão algébrica que representa a área do forro após ser lavado é (5 – x) (3 – y).
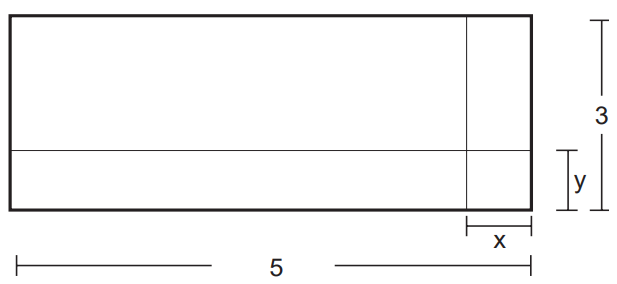
Nessas condições, a área perdida do forro, após a primeira lavagem, será expressa por:
A) 2xy
B) 15 − 3x
C) 15 − 5y
D) -5y − 3x
E) 5y + 3x – xy
Alternativa E
Sabemos que a área do retângulo é dada pela multiplicação dos seus dois lados.
A área perdida é dada pelo retângulo com 5 unidades de comprimento e y de largura e o retângulo que tem x unidades de comprimento e 3 unidades de largura. Logo, as áreas desses retângulos são, respectivamente, 5y e 3x. Entretanto, podemos perceber que existe uma área que pertence aos dois triângulos, com x unidades de comprimento e y unidades de largura, ou seja, de área xy. Então, a área que diminuiu será de:
\(5y+3x - xy\)
