Exercícios sobre multiplicação de matrizes
Resolva esta lista de exercícios sobre multiplicação de matrizes e avalie seus conhecimentos sobre o assunto.
Publicado por: Raul Rodrigues de OliveiraQuestões
-
Questão 1
Dada a matriz \(A = \begin{pmatrix} 1 & 2 \\ 3 & 4 \end{pmatrix} \) e a matriz \(B = \begin{pmatrix} 5 & -1 \\ 0 & -2 \end{pmatrix} \), considerando C = A ⋅ B, o termo c12 será igual a:
Alternativa D.
Calculando a multiplicação de matrizes, temos que:
\(c_{12} = 1 \cdot (-1) + 2 \cdot (-2)\)
\(c_{12} = -1 - 4 = -5\)
-
Questão 2
Dadas as matrizes A e B:
\(A = \pmatrix {1 & 3 & 5 \\ 2 & 4 & 6} e\ B = \pmatrix {3 \\ 2 \\ 1}\)
Sendo C = A ⋅ B, o valor da soma c11+c21 é:
Alternativa C.
Calculando a multiplicação, temos que:
\(c_{11} = 1\cdot 3 + 3\cdot 2 + 5\cdot 1 = 3 + 6 + 5 = 14\)
\(c_{21} = 2\cdot 3 + 4\cdot 2 + 6\cdot 1 = 6 + 8 + 6 = 20\)
A soma 14 + 20 = 34.
-
Questão 3
Dada as matrizes:
\(A = \pmatrix {1 & -1 & 2\\ 0 & 2 & 1} e\ B = \pmatrix {4 & -1\\ x & 0\\ 1 & 2}\)
Sabendo que:
\(A \cdot B = \pmatrix {3 & 3 \\ 7 & 2}\)
O valor de x é:
Alternativa D.
Calculando o produto entre a primeira linha e a primeira coluna das matrizes A e B respectivamente, temos que:
\(1 \cdot 4 + (-1) \cdot x + 2\cdot 1 = 3\)
\(4 - x + 2 = 3\)
\(- x = 3 - 4 -2 \)
\(-x = -3\)
\(x = 3\)
-
Questão 4
(UFRGS) A matriz C fornece, em reais, o custo das porções de arroz, carne e salada usados em um restaurante. A matriz P fornece o número de porções de arroz, carne e salada usados na composição dos pratos tipo P1, P2 e P3.
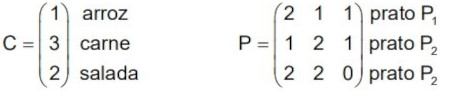
A matriz que fornece o custo de produção, em reais, dos pratos P1, P2 e P3 é
Alternativa A.
Calculando o produto, temos que:
\(\begin{pmatrix} 2 \cdot 1 + 1 \cdot 3 + 1 \cdot 2 & \\ 1 \cdot 1 + 2 \cdot 3 + 1 \cdot 2 & \\ 2 \cdot 1 + 2 \cdot 3 + 0 \cdot 2 \end{pmatrix} = \begin{pmatrix} 2 + 3 + 2 \\ 1 + 6 + 2 \\ 2 + 6 + 0 \end{pmatrix} = \begin{pmatrix} 7 \\ 9 \\ 8 \end{pmatrix} \)
-
Questão 5
(Técnico Judiciário - Auxiliar - Secretaria) A matriz X fornece, em reais, o custo das porções de carne, macarrão e salada usadas em um restaurante.
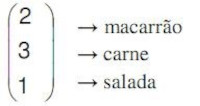
A matriz Y fornece o número de porções de macarrão, carne e salada usadas na composição dos pratos A1, A2 e A3 desse restaurante.
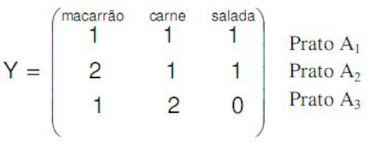
Qual é a matriz que representa o custo de produção, em reais, dos pratos A1, A2 e A3?
Alternativa A.
Calculando o produto, temos que:
\(\begin{pmatrix} 1 \cdot 2 + 1 \cdot 3 + 1 \cdot 1 \\ 2 \cdot 2 + 1 \cdot 3 + 1 \cdot 1 \\ 1 \cdot 2 + 2 \cdot 3 + 0 \cdot 1 \end{pmatrix} = \begin{pmatrix} 2 + 3 + 1 \\ 4 + 3 + 1 \\ 2 + 6 + 0 \end{pmatrix} = \begin{pmatrix} 6 \\ 8 \\ 8 \end{pmatrix} \)
-
Questão 6
Ao multiplicar as matrizes A3x2 e B2x3, o produto dessas matrizes A ⋅ B vai gerar uma matriz C que possui:
Alternativa A.
O resultado do produto entre duas matrizes possui número de linha igual ao número de linhas da primeira matriz e o número de colunas da segunda matriz, logo ele terá 3 linhas e 3 colunas.
-
Questão 7
Sobre a multiplicação de matrizes, marque a alternativa correta:
Alternativa B.
A matriz produto terá o número de linhas da primeira matriz e o número de colunas da segunda matriz, a alternativa que demonstra isso corretamente é a alternativa B: A3x1 ⋅ B1x2 = C3x2.
-
Questão 8
Para que a multiplicação AB seja definida, o número de colunas da matriz A deve ser igual ao número de:
Alternativa C.
Para que a multiplicação AB seja definida, o número de colunas de A deve ser igual ao número de linhas de B.
-
Questão 9
Sendo A uma matriz quadrada de ordem 2, dada por \(A = \begin{bmatrix} 0 & 1 \\ -1 & 0 \end{bmatrix} \), qual é o resultado de A ⋅ A?
Alternativa C.
Calculando o produto: \(\begin{bmatrix} 0 & 1 \\ -1 & 0 \end{bmatrix} \cdot \begin{bmatrix} 0 & 1 \\ -1 & 0 \end{bmatrix} \) , temos que:
\(A \cdot A = \begin{bmatrix} 0 \cdot 0 + 1 \cdot (-1) & 0 \cdot 1 + 1 \cdot 0 \\ -1 \cdot 0 + (-1) \cdot 0 & -1 \cdot 1 + 0 \cdot 0 \end{bmatrix} = \begin{bmatrix} -1 & 0 \\ 0 & -1 \end{bmatrix} \)
-
Questão 10
Considere a matriz A de ordem 2×3 e a matriz B de ordem 3×2. Qual será a ordem do produto AB?
Alternativa A.
O produto de uma matriz m×n por uma matriz n×p resulta em uma matriz de ordem m×p. Portanto, 2×3 multiplicado por 3×2 resulta em 2×2.
-
Questão 11
Uma empresa possui três fábricas que produzem três tipos diferentes de produtos (A, B e C). A matriz P, representando a produção semanal (em unidades) de cada fábrica, é dada por:
\(P = \begin{pmatrix} 100 & 200 & 150 \\ 80 & 120 & 90 \\ 50 & 60 & 70 \end{pmatrix} \)
Sendo que cada linha representa uma fábrica e cada coluna representa um produto. O custo por unidade de cada produto é dado pela matriz:
\(C = \begin{pmatrix} 5 \\ 10 \\ 8 \end{pmatrix} \)
Qual será o custo total de produção para cada fábrica?
Alternativa A.
Calculando o produto entre as matrizes, temos que:
\(\begin{pmatrix} 100 \cdot 5 + 200 \cdot 10 + 150 \cdot 8 \\ 80 \cdot 5 + 120 \cdot 10 + 90 \cdot 8 \\ 50 \cdot 5 + 60 \cdot 10 + 70 \cdot 8 \end{pmatrix} = \begin{pmatrix} 3900 \\ 2200 \\ 1360 \end{pmatrix} \)
-
Questão 12
Considere as seguintes afirmativas sobre multiplicação de matrizes:
I. Para que duas matrizes possam ser multiplicadas, o número de colunas da primeira matriz deve ser igual ao número de linhas da segunda matriz.
II. A multiplicação de matrizes é comutativa, ou seja, se A×B é definido, então B×A também será definido e os resultados serão iguais.
III. O produto de duas matrizes A e B terá o mesmo número de linhas de A e o mesmo número de colunas de B.Qual das opções abaixo está correta?
Alternativa C.
- A afirmativa I é verdadeira, pois a condição para multiplicar duas matrizes é que o número de colunas da primeira seja igual ao número de linhas da segunda.
- A afirmativa II é falsa, pois a multiplicação de matrizes não é comutativa; mesmo que A×B e B×A sejam definidos, o resultado pode ser diferente.
- A afirmativa III é verdadeira, já que o produto resultante de A×B terá o mesmo número de linhas de A e o mesmo número de colunas de B.